Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper/Viertes Buch
| ← Drittes Buch Teil B | Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper (1879) von Nicolaus Copernicus |
Fünftes Buch Teil A → |
Nachdem wir in dem vorigen Buche, soviel unsere schwache Kraft vermochte, die Erscheinungen auseinander gesetzt haben, welche wegen der Bewegung der Erde um die Sonne stattfinden; und da es nun unsere Aufgabe ist, die Bewegungen aller Wandelsterne aus derselben Ursache herzuleiten: so mag jetzt der Lauf des Mondes zur Sprache kommen, und zwar deswegen, weil durch ihn, der am Tage und an der Nacht betheiligt ist, die Oerter der Sterne vorzüglich gemessen und untersucht werden; ferner weil von Allen er allein seine, freilich gleichfalls ungleichmässigen, Bewegungen im Ganzen auf den Mittelpunkt der Erde bezieht, und der Erde am verwandtesten ist, und daher an ihm, nichts von der Bewegung der Erde, ausser etwa der täglichen, bemerkt wird; so dass man aus diesem Grunde um so mehr geglaubt hat, die Erde sei der Mittelpunkt der Welt, und der gemeinsame Mittelpunkt aller Bewegungen. Wir werden zwar bei der Ableitung des Mondlaufes, insofern er um die Erde vor sich geht, von den Meinungen der Alten uns nicht entfernen, müssen aber noch einiges Andere anführen, was wir von den Alten nicht empfangen haben, was mehr im Einklange steht, und wodurch wir die Mondbewegung, so viel als möglich sicherer feststellen.
Der Mondlauf hat das Eigenthümliche, dass er nicht den mittleren Kreis der Zeichen beschreibt, sondern einen eignen geneigten Kreis, welcher jenen in zwei gleiche Hälften theilt, und von jenem wiederum selbst geschnitten wird, wodurch er in beide Breiten übergeht. Dies verhält sich fast so, wie die Sonnenwenden bei der jährlichen Bewegung, so dass das, was für die Sonne das Jahr, für den Mond der Monat ist. Die mittleren Schnittpunkte der Ekliptik werden von Einigen Knoten genannt, und die Conjunctionen und Oppositionen von Sonne und Mond, wenn sie mit diesen zusammentreffen, heissen ekliptische; es sind beiden Kreisen keine andern
[194] Punkte als diese gemeinsam, und in diesen können Sonnen- und Mond-Finsternisse eintreten. In den andern Punkten bewirkt die Abweichung des Mondes, dass sie sich gegenseitig nicht verfinstern, noch im Vorbeigehn sich verdecken. Diese schiefe Mondbahn bewegt sich mit ihren vier Hauptpunkten gleichmässig um den Mittelpunkt der Erde, täglich um ungefähr 3′, und vollendet in 19 Jahren ihren Umlauf. In dieser Bahn und in dieser Ebene sieht man den Mond sich immer rechtläufig bewegen, aber bald sehr langsam, bald sehr geschwind. Nämlich um so langsamer, je entfernter, und um so geschwinder, je näher er der Erde ist, was an ihm leichter, als an irgend einem andern Gestirne, eben wegen seiner Nähe, erkannt werden konnte. Man nahm daher an, dass dies durch einen Epicykel entstände, indem der Mond, beim Durchlaufen desselben, in dem obern Bogen in seiner gleichförmigen Bewegung verzögert, in dem untern aber beschleunigt würde. Dass nun dasjenige, was durch den Epicykel geschieht, auch durch einen excentrischen Kreis geschehen kann, ist nachgewiesen[1]; man zog den Epicykel deswegen vor, weil der Mond eine doppelte Ungleichmässigkeit zu haben schien. Wenn er nämlich in der grössten oder kleinsten Abside des Epicykels stand: so trat eine Abweichung von der gleichmässigen Bewegung gar nicht, an den Schnittpunkten des Epicykels dagegen nicht in gleicher Weise hervor, dieselbe war nämlich weit grösser bei den Vierteln des zunehmenden oder abnehmenden Mondes, als wenn er voll oder neu war, und dies in einer bestimmten und regelmässigen Aufeinanderfolge. Deshalb nahm man an, der Kreis, in welchem der Epicykel sich bewege, habe mit der Erde nicht denselben Mittelpunkt; sondern der Mond bewege sich in einem excentrischen Epicykel nach dem Gesetze, dass bei allen mittleren Oppositionen und Conjunctionen der Sonne und des Mondes der Epicykel im Apogeum des excentrischen Kreises, bei den dazwischenliegenden Quadraturen aber in dessen Perigeum stehe.
[195] Mittelpunkt des Epicykels . Nun bewege sich das Apogeum des excentrischen Kreises rückläufig, der Epicykel aber rechtläufig, beide gleicherweise um in gleichmässigen und monatlichen Umläufen in Bezug auf die mittleren Conjunctionen oder Oppositionen, und die Linie des mittleren Ortes der Sonne bleibe immer in der Mitte zwischen Beiden. Der Mond aber gehe wieder rückläufig von dem Apogeum des Epicykels. Wenn dies so festgesetzt wäre, meinen sie, stimme die Erscheinung damit überein. Wenn nämlich der Epicykel in einem halben Jahre zwar von der Sonne einen Halbkreis, vom Apogeum aber einen ganzen Umlauf vollendet: so folgt, dass in der Mitte dieser Zeit, d. h um die Zeit der Quadratur, beide in dem Durchmesser sich einander gegenüberstehen, und der Epicykel im excentrischen Kreise perigeisch wird, wie im Punkte , wo er, der Erde näher gekommen, grössere Unterschiede der Ungleichmässigkeit hervorbringt. Denn wenn gleiche Grössen in ungleichen Entfernungen sich befinden, so erscheinen die dem Auge näheren, grösser. Sie waren also, als der Epicykel in stand, am kleinsten, in dagegen am grössten, weil das Verhältniss des Durchmessers des Epicykels zur Linie am kleinsten, zu am grössten von allen Uebrigen an andern Oertern ist, indem die kürzeste, gleich die längste von allen Linien ist, welche vom Mittelpunkte der Erde nach dem excentrischen Kreise gezogen werden können.

[196] fest, dass bei der Quadratur des Mondes jeder von beiden Bogen, und , ein Halbkreis ist: folglich ist die Bewegung des Epicykels auf seinem excentrischen Kreise, welchen er beschreibt, ungleichmässig. Wenn dies aber so wäre, was sollten wir dann zu dem Grundsatze sagen, dass die Bewegung der himmlischen Körper gleichmässig ist, auch wenn sie ungleichmässig erscheint? Wenn nun die Bewegung des Epicykels gleichmässig erschiene, so müsste sie in der That ungleichmässig sein; es würde also das grade Gegentheil von dem zu Grunde gelegten und angenommenen Principe stattfinden. Wenn man aber einwenden wollte, dass sich der Mittelpunkt des Epicykels um den Mittelpunkt der Erde gleichmässig bewege, und dies hinreiche, um die Gleichmässigkeit zu wahren: so fragen wir, wie kommt jene Gleichmässigkeit in einen andern Kreis, da doch in diesem seine Bewegung nicht stattfindet, sondern in dem excentrischen? Ebenso setzt uns auch das mit Recht in Verwunderung, dass man die Gleichmässigkeit des Mondes selbst in dessen Epicykel, nicht in Beziehung auf den Mittelpunkt der Erde, also durch die Linie , auf welche doch die Gleichmässigkeit eigentlich bezogen werden müsste, indem dieselbe mit dem Mittelpunkte des Epicykels zusammenstimmt, erkannt wissen will; sondern in Bezug auf einen beliebigen andern Punkt, und dass man behauptet, zwischen diesem und dem Mittelpunkte des excentrischen Kreises stehe die Erde in der Mitte, und die Linie sei gleichsam ein Index der Gleichmässigkeit des Mondes im Epicykel, was ebenfalls in der That hinreicht, diese Bewegung als ungleichmässig zu erweisen. Die Erscheinungen, welche zum Theil aus dieser Hypothese folgen, nöthigen zu diesem Eingeständniss. Ebenso gut könnten wir auch untersuchen, wie die Beweisführung ausfallen würde, wenn wir, indem der Mond seinen Epicykel ungleichmässig durchliefe, die ungleichmässige Erscheinung aus der ungleichmässigen Bewegung erklären wollten. Was würden wir Anderes thun, als Denen eine Handhabe darbieten, welche unsere Wissenschaft herabsetzen? Ferner belehren uns die Erfahrung und selbst die Anschauung, dass die Parallaxen des Mondes, welche die Berechnung jener Kreise ergiebt, nicht damit im Einklange stehen. Es entstehen nämlich die Parallaxen, welche man Commutationen nennt, aus der im Vergleich zur Entfernung des Mondes sehr bemerkbaren Grösse der Erde. Wenn man nämlich von der Oberfläche und vom Mittelpunkte der Erde nach dem Monde grade Linien zieht, so werden dieselben nicht parallel erscheinen, sondern sich unter einem merklichen Winkel im Mondkörper schneiden. Dies muss nothwendig eine Verschiedenheit in der Erscheinung des Mondes bewirken, so dass derselbe denen, die ihn von der Oberfläche der Erde in schräger Richtung beobachten, an einer andern Stelle erscheint, als Denen, welche ihn vom Mittelpunkte aus, also in ihrem Scheitel erblicken. Diese Commutationen sind nach Verhältniss der Entfernung des Mondes von der Erde verschieden. Nach Uebereinstimmung aller Mathematiker ist die grösste Entfernung 641/6 Erdhalbmesser; nach dem Maasse Jener aber müsste die kleinste 3311/20 betragen, so dass der Mond fast auf die halbe Entfernung [197] sich uns näherte, und nach folgerichtigem Schlusse müssten sich die Parallaxen in der kleinsten und grössten Entfernung um ungefähr das Doppelte von einander unterscheiden. Wir sehen aber, dass die Parallaxen, welche den Quadraturen des zunehmenden und abnehmenden Mondes entsprechen, selbst im Perigeum des Epicykels, sich sehr wenig oder gar nicht unterscheiden, von denen, welche bei Sonnen- und Mond-Finsternissen eintreten, wie wir an seiner Stelle hinlänglich erweisen werden. Am meisten beweist den Irrthum der Körper des Mondes selbst, welcher aus gleichem Grunde, seinem Durchmesser nach doppelt so gross oder doppelt so klein gesehen werden müsste. Da sich aber die Kreise wie die Quadrate ihrer Durchmesser verhalten, so müsste der Mond, wenn er in den Quadraturen der Erde am nächsten stände, viermal so gross erscheinen, als wenn er in seiner Opposition mit der Sonne voll wäre; und wenn er mit seiner Hälfte schiene, müsste er nichts desto weniger zweimal so hell scheinen, als wenn er voll wäre. Wenn Jemand, obgleich das Gegentheil hiervon für sich klar ist, dennoch mit dem blossen Augenscheine sich nicht begnügen, sondern dies durch das Hipparchische Diopter, oder durch andere Instrumente, mittelst welcher der Durchmesser des Mondes gemessen wird, untersuchen wollte, der würde finden, dass sich derselbe nur um so viel unterscheidet, als es der Epicykel, ohne jenen excentrischen Kreis verlangt. Deshalb nahmen Menelaus und Timochares bei ihren Untersuchungen der Fixsterne durch den Ort des Mondes keinen Anstand, immer denselben Durchmesser des Mondes anzuwenden, nämlich die Hälfte eines Grades, indem der Mond meist so viel einzunehmen scheint.
So scheint denn in der That der Kreis, durch welchen der Epicykel grösser oder kleiner erscheint, kein excentrischer zu sein, sondern einer andern Art von Kreisen anzugehören. Es sei nämlich ein Epicykel, welchen wir den ersten und grössern nennen wollen, sein Mittelpunkt ; von dem Mittelpunkte der Erde, welcher in liegt, werde die grade Linie bis zur grössten Abside des Epicykels verlängert; um diesen Punkt werde ein anderer kleinerer Epicykel beschrieben; und Alles dies liege in derselben Ebene der schiefen Mondbahn. Es bewege sich rechtläufig, dagegen rückläufig, und der Mond von aus im oberen Theile von wieder rechtläufig; und zwar nach der Regel, dass, während die Linie mit dem mittleren Orte der Sonne zusammenfällt, der Mond immer dem Mittelpunkte am nächsten, d. h. in sich befindet, in den Quadraturen dagegen am entferntesten, also in . Wenn man dies zum Grunde legt, so behaupte ich, stehen die Monderscheinungen damit im Einklange. Es ergiebt sich nämlich, dass der Mond den kleinen Epicykel zweimal in einem Monate durchläuft, in welcher Zeit einmal zur Sonne zurückkehrt; und der Neu-
[198]
[199] von der Sonne durch den Mittelpunkt der Erde liegt. Deswegen sind die Mondfinsternisse am geeignetsten, um durch sie auf die sicherste Weise den Lauf des Mondes zu bestimmen.
Unter den Aeltesten, denen es am Herzen lag, der Nachwelt über diesen Gegenstand Zahlenangaben zu überliefern, findet sich der Athenienser Meton, welcher um die sieben und dreissigste Olympiade blühete. Dieser gab an, dass in 19 Sonnenjahren 235 Monate ablaufen, deswegen wird dieses grosse Jahr die Meton’sche Enneadekateris, d. h. neunzehnjährige Periode, genannt. Die Zahl fand so grossen Beifall, dass sie zu Athen und in andern ausgezeichneten Städten auf dem Markte angeschlagen wurde, wie dieselbe denn auch bis auf die Gegenwart im gewöhnlichen Leben angenommen wird, weil man glaubt, dass durch sie der Anfang und das Ende der Monate nach einer sichern Regel festständen. Es ist auch das Sonnenjahr von 365 ¼ Tagen dieser Anzahl von Monaten commensurabel. Hiervon rührt jene Callippische Periode von 76 Jahren her, in welcher neunzehnmal ein Tag eingeschaltet wird, und welche man das Callippische Jahr genannt hat. Aber das Genie Hipparch’s fand, dass in 304 Jahren ein ganzer Tag zu viel entstände, und dass dies nur dadurch corrigirt würde, wenn man das Sonnenjahr um den 300sten Theil eines Tages verkleinerte. Daher ist dieser Zeitraum von Einigen[3] das grosse Jahr des Hipparch genannt worden, in welchem 3760 Monate ablaufen. Dies ist aber oberflächlich und ohne Genauigkeit gesagt, deshalb hat derselbe Hipparch über die Zeit, in welcher die Anomalie mit der Breite zugleich wiederkehrt, eine nähere Untersuchung angestellt, und, — nach Vergleichung seiner Aufzeichnungen über die von ihm sehr sorgfältig angestellten Beobachtungen der Mondfinsternisse, mit denen der Chaldäer, — die Zeit, in welcher die monatlichen Bewegungen mit denen der Anomalie zugleich wiederkehren, zu 345 ägyptischen Jahren 82 Tagen und 1 Stunde bestimmt, und in dieser Zeit sollten 4267 Monate, aber 4573 Umläufe der Anomalie vollendet werden. Wenn daher durch die Zahl der Monate, die Anzahl der Tage, welche 126007 Tage und 1 Stunde beträgt, dividirt wird: so erhält man einen Monat gleich 29 Tage 31I 50II 8III 9IV 20V [4]. Hiernach ergab sich die Bewegung für jede beliebige Zeit. Denn dividirt man die 360° eines monatlichen Umlaufs durch die Dauer eines Monats, so ergiebt sich der tägliche Lauf des Mondes gegen die Sonne zu 12° 11′ 26″ 41‴ 20IV 18V [5]. Dies 365 mal genommen, ergiebt die jährliche Bewegung zu 12 ganzen Umläufen 129° 37′ 21″ 28‴ 29⁗[6]. Da ferner 4267 Monate und 4573 Umläufe der Anomalie den gemeinsamen Factor 17 enthalten: so ist ihr Verhältniss in den kleinsten Zahlen ausgedrückt 251 zu 269, in welchem Verhältnisse wir [200] also, nach dem 15ten Satze des 5ten Buches von Euklid, dasjenige des Mondlaufs zur Bewegung der Anomalie haben. So dass, wenn wir die Bewegung des Mondes mit 269 multipliciren und das Produkt mit 251 dividiren, die jährliche Bewegung der Anomalie sich ergiebt zu: 13 ganzen Umläufen 88° 43′ 8″ 40‴ 20⁗[7] und daraus die tägliche zu 13° 3′ 53″ 56‴ 29⁗[7]. Der Umlauf der Breite hat aber ein anderes Verhältniss und trifft nicht mit der Zeit zusammen, in welcher die Anomalie wiederkehrt, sondern nur dann sieht man die Breite des Mondes wiederkehren, wenn eine spätere Mondfinsterniss einer früheren in Allem ähnlich und gleich ist, wenn also bei beiden von derselben Seite her, sowohl der Grösse als auch der Dauer nach, gleiche Verfinsterungen stattfinden; was der Fall ist, wenn der Mond von der grössten oder von der kleinsten Abside gleiche Abstände hat. Denn alsdann ist klar, dass der Mond gleiche Schatten in gleicher Zeit durchläuft. Eine solche Wiederkehr ereignet sich nach Hipparch in 5458 Monaten, denen 5923 Umläufe der Breite entsprechen. Nach diesem Verhältnisse sind die besondern Bewegungen für Jahre und Tage, wie früher berechnet. Wenn wir nämlich die Bewegung des Mondes von der Sonne mit 5923 multipliciren und das Produkt durch 5458 dividiren: so erhalten wir als Bewegung der Breite des Mondes für ein Jahr: 13 Umläufe 148° 42′ 46″ 49‴ 3⁗[8] und für einen Tag: 13° 13′ 45″ 39‴ 40⁗[9]. Auf diese Weise ermittelte Hipparch die gleichmässigen Bewegungen des Mondes, und Niemand kam denselben näher, als er. Dass man jedoch bei allen diesen Zahlen noch etwas übersehen hatte, haben die spätern Jahrhunderte erwiesen. Ptolemäus nämlich fand zwar dieselbe mittlere Bewegung des Mondes von der Sonne, wie Hipparch, aber die jährliche Bewegung der Anomalie fand er um 1″ 11‴ 39⁗[10] kleiner, die jährliche Bewegung der Breite aber um 53‴ 41⁗ grösser. Wir aber haben, nach dem Verlaufe einer sehr grossen Zeit, die mittlere jährliche Bewegung des Hipparch um 1″ 2‴ 49⁗ zu klein gefunden, der Bewegung der Anomalie Hipparchs aber fehlen nur 24‴ 49⁗. Die Bewegung der Breite Hipparchs ist aber zu gross um 1″ 1‴ 44⁗. Dadurch wird dasjenige, um was die jährliche gleichmässige Bewegung des Mondes sich von der jährlichen Bewegung der Erde unterscheidet 129° 37′ 22″ 32‴ 40⁗, die Bewegung der Anomalie 88° 43′ 9″ 5‴ 9⁗, die Bewegung der Breite 148° 42′ 45″ 17‴ 21⁗ [11].
[201]| Aegyptische Jahre | Bewegung | Ort Christi 3 S. 29° 58′ Cap. 7. | Aegyptische Jahre | Bewegung | ||||||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | |||||
| Sec. | Tert. | Sec. | Tert. | |||||||||||||
| 1 | 2 | 9 | 37 | 22 | 36 | 22 | 32 | 31 | 0 | 58 | 18 | 40 | 48 | 38 | 52 | |
| 2 | 4 | 19 | 14 | 45 | 12 | 45 | 5 | 32 | 3 | 7 | 56 | 3 | 25 | 1 | 25 | |
| 3 | 0 | 28 | 52 | 7 | 49 | 7 | 38 | 33 | 5 | 17 | 33 | 26 | 1 | 23 | 58 | |
| 4 | 2 | 38 | 29 | 30 | 25 | 30 | 10 | 34 | 1 | 27 | 10 | 48 | 38 | 46 | 30 | |
| 5 | 4 | 48 | 6 | 53 | 2 | 53 | 43 | 35 | 3 | 36 | 48 | 11 | 14 | 9 | 3 | |
| 6 | 0 | 57 | 44 | 15 | 38 | 15 | 16 | 36 | 5 | 46 | 25 | 33 | 51 | 31 | 36 | |
| 7 | 3 | 7 | 21 | 38 | 14 | 37 | 48 | 37 | 1 | 56 | 2 | 56 | 27 | 54 | 8 | |
| 8 | 5 | 16 | 59 | 0 | 51 | 0 | 21 | 38 | 4 | 5 | 40 | 19 | 3 | 16 | 41 | |
| 9 | 1 | 26 | 36 | 23 | 27 | 22 | 54 | 39 | 0 | 15 | 17 | 41 | 40 | 39 | 14 | |
| 10 | 3 | 36 | 13 | 46 | 4 | 45 | 26 | 40 | 2 | 24 | 55 | 4 | 16 | 1 | 46 | |
| 11 | 5 | 45 | 51 | 8 | 40 | 7 | 59 | 41 | 4 | 34 | 32 | 26 | 53 | 24 | 19 | |
| 12 | 1 | 55 | 28 | 31 | 17 | 31 | 32 | 42 | 0 | 44 | 9 | 49 | 29 | 46 | 52 | |
| 13 | 4 | 5 | 5 | 53 | 53 | 53 | 4 | 43 | 2 | 53 | 47 | 12 | 5 | 9 | 24 | |
| 14 | 0 | 14 | 43 | 16 | 29 | 15 | 37 | 44 | 5 | 3 | 24 | 34 | 42 | 31 | 57 | |
| 15 | 2 | 24 | 20 | 39 | 6 | 38 | 10 | 45 | 1 | 13 | 1 | 57 | 18 | 54 | 30 | |
| 16 | 4 | 33 | 58 | 1 | 42 | 0 | 42 | 46 | 3 | 22 | 39 | 19 | 55 | 17 | 2 | |
| 17 | 0 | 43 | 35 | 24 | 19 | 23 | 15 | 47 | 5 | 32 | 16 | 42 | 31 | 39 | 35 | |
| 18 | 2 | 53 | 12 | 46 | 55 | 45 | 48 | 48 | 1 | 41 | 54 | 5 | 8 | 2 | 8 | |
| 19 | 5 | 2 | 50 | 9 | 31 | 8 | 20 | 59 | 3 | 51 | 31 | 27 | 44 | 24 | 40 | |
| 20 | 1 | 12 | 27 | 32 | 8 | 30 | 53 | 50 | 0 | 1 | 8 | 50 | 20 | 47 | 13 | |
| 21 | 3 | 22 | 4 | 54 | 14 | 53 | 26 | 51 | 2 | 10 | 46 | 12 | 57 | 9 | 46 | |
| 22 | 5 | 31 | 42 | 17 | 21 | 15 | 58 | 52 | 4 | 20 | 23 | 35 | 33 | 32 | 18 | |
| 23 | 1 | 41 | 19 | 39 | 57 | 38 | 31 | 53 | 0 | 30 | 0 | 58 | 10 | 54 | 51 | |
| 24 | 3 | 50 | 57 | 2 | 34 | 1 | 4 | 54 | 2 | 39 | 38 | 20 | 46 | 17 | 24 | |
| 25 | 0 | 0 | 34 | 25 | 10 | 23 | 36 | 55 | 4 | 49 | 15 | 43 | 22 | 39 | 56 | |
| 26 | 2 | 10 | 11 | 47 | 46 | 46 | 9 | 56 | 0 | 58 | 53 | 5 | 59 | 2 | 29 | |
| 27 | 4 | 19 | 49 | 10 | 23 | 8 | 42 | 57 | 3 | 8 | 30 | 28 | 35 | 25 | 2 | |
| 28 | 0 | 29 | 26 | 32 | 59 | 31 | 14 | 58 | 5 | 18 | 7 | 51 | 12 | 47 | 34 | |
| 29 | 2 | 39 | 3 | 55 | 36 | 53 | 47 | 59 | 1 | 27 | 45 | 13 | 48 | 0 | 7 | |
| 30 | 4 | 48 | 41 | 18 | 12 | 16 | 20 | 60 | 3 | 37 | 22 | 36 | 25 | 32 | 40 | |
| Tage | Bewegung | Tage | Bewegung | |||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Sechzig | Grad | Min. | Secund. | Tertien | |||
| 1 | 0 | 12 | 11 | 26 | 41 | 31 | 6 | 17 | 54 | 47 | 26 | |
| 2 | 0 | 24 | 22 | 53 | 23 | 32 | 6 | 30 | 6 | 14 | 8 | |
| 3 | 0 | 36 | 34 | 20 | 4 | 33 | 6 | 42 | 17 | 40 | 49 | |
| 4 | 0 | 48 | 45 | 46 | 46 | 34 | 6 | 54 | 29 | 7 | 31 | |
| 5 | 1 | 0 | 57 | 13 | 27 | 35 | 7 | 6 | 40 | 34 | 12 | |
| 6 | 1 | 13 | 8 | 40 | 9 | 36 | 7 | 18 | 52 | 0 | 54 | |
| 7 | 1 | 25 | 20 | 6 | 50 | 37 | 7 | 31 | 3 | 27 | 35 | |
| 8 | 1 | 37 | 31 | 33 | 32 | 38 | 7 | 43 | 14 | 54 | 17 | |
| 9 | 1 | 49 | 43 | 0 | 13 | 39 | 7 | 55 | 26 | 20 | 58 | |
| 10 | 2 | 1 | 54 | 26 | 55 | 40 | 8 | 7 | 37 | 47 | 40 | |
| 11 | 2 | 14 | 5 | 53 | 36 | 41 | 8 | 19 | 49 | 14 | 21 | |
| 12 | 2 | 26 | 17 | 20 | 18 | 42 | 8 | 32 | 0 | 41 | 3 | |
| 13 | 2 | 38 | 28 | 47 | 0 | 43 | 8 | 44 | 12 | 7 | 44 | |
| 14 | 2 | 50 | 40 | 13 | 41 | 44 | 8 | 56 | 23 | 34 | 26 | |
| 15 | 3 | 2 | 51 | 40 | 22 | 45 | 9 | 8 | 35 | 1 | 7 | |
| 16 | 3 | 15 | 3 | 7 | 4 | 46 | 9 | 20 | 46 | 27 | 49 | |
| 17 | 3 | 27 | 14 | 33 | 45 | 47 | 9 | 32 | 57 | 54 | 30 | |
| 18 | 3 | 39 | 26 | 0 | 27 | 48 | 9 | 45 | 9 | 21 | 12 | |
| 19 | 3 | 51 | 37 | 27 | 8 | 49 | 9 | 57 | 20 | 47 | 53 | |
| 20 | 4 | 3 | 48 | 53 | 50 | 50 | 10 | 9 | 32 | 14 | 35 | |
| 21 | 4 | 16 | 0 | 20 | 31 | 51 | 10 | 21 | 43 | 41 | 16 | |
| 22 | 4 | 28 | 11 | 47 | 13 | 52 | 10 | 33 | 55 | 7 | 58 | |
| 23 | 4 | 40 | 23 | 13 | 54 | 53 | 10 | 46 | 6 | 34 | 40 | |
| 24 | 4 | 52 | 34 | 40 | 36 | 54 | 10 | 58 | 18 | 1 | 21 | |
| 25 | 5 | 4 | 46 | 7 | 17 | 55 | 11 | 10 | 29 | 28 | 2 | |
| 26 | 5 | 16 | 57 | 33 | 59 | 56 | 11 | 22 | 40 | 54 | 43 | |
| 27 | 5 | 29 | 9 | 0 | 40 | 57 | 11 | 34 | 52 | 21 | 25 | |
| 28 | 5 | 41 | 20 | 27 | 22 | 58 | 11 | 47 | 3 | 48 | 7 | |
| 29 | 5 | 53 | 31 | 54 | 3 | 59 | 11 | 59 | 15 | 14 | 48 | |
| 30 | 6 | 5 | 43 | 20 | 45 | 60 | 12 | 11 | 26 | 41 | 31 | |
| Aegyptische Jahre | Bewegung | Ort Christi 3 S. 27° 7′ Cap. 7 | Aegyptische Jahre | Bewegung | ||||||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | |||||
| Sec. | Tert. | Sec. | Tert. | |||||||||||||
| 1 | 1 | 28 | 43 | 9 | 7 | 9 | 5 | 31 | 3 | 50 | 17 | 42 | 44 | 41 | 39 | |
| 2 | 2 | 57 | 26 | 18 | 14 | 18 | 10 | 32 | 5 | 19 | 0 | 51 | 52 | 50 | 44 | |
| 3 | 4 | 26 | 9 | 27 | 21 | 27 | 15 | 33 | 0 | 47 | 43 | 0 | 59 | 59 | 49 | |
| 4 | 5 | 54 | 52 | 36 | 29 | 36 | 20 | 34 | 2 | 16 | 27 | 10 | 6 | 8 | 55 | |
| 5 | 1 | 23 | 35 | 45 | 36 | 45 | 25 | 35 | 3 | 45 | 10 | 19 | 13 | 18 | 0 | |
| 6 | 2 | 52 | 18 | 54 | 43 | 54 | 30 | 36 | 5 | 13 | 53 | 28 | 21 | 27 | 5 | |
| 7 | 4 | 21 | 2 | 3 | 59 | 3 | 36 | 37 | 0 | 42 | 36 | 37 | 28 | 36 | 10 | |
| 8 | 5 | 49 | 45 | 12 | 58 | 12 | 41 | 38 | 2 | 11 | 19 | 46 | 35 | 45 | 15 | |
| 9 | 1 | 18 | 28 | 22 | 5 | 21 | 46 | 39 | 3 | 40 | 2 | 55 | 42 | 54 | 20 | |
| 10 | 2 | 47 | 11 | 31 | 12 | 30 | 51 | 40 | 5 | 8 | 46 | 4 | 50 | 3 | 26 | |
| 11 | 4 | 15 | 54 | 40 | 19 | 39 | 56 | 41 | 0 | 37 | 29 | 13 | 57 | 12 | 31 | |
| 12 | 5 | 44 | 37 | 49 | 27 | 49 | 1 | 42 | 2 | 6 | 12 | 23 | 4 | 21 | 36 | |
| 13 | 1 | 13 | 20 | 58 | 34 | 58 | 6 | 43 | 3 | 34 | 55 | 32 | 11 | 30 | 41 | |
| 14 | 2 | 42 | 4 | 7 | 41 | 7 | 12 | 44 | 5 | 3 | 38 | 41 | 19 | 39 | 46 | |
| 15 | 4 | 10 | 47 | 16 | 48 | 16 | 17 | 45 | 0 | 32 | 21 | 50 | 26 | 48 | 51 | |
| 16 | 5 | 39 | 30 | 25 | 56 | 25 | 22 | 46 | 2 | 1 | 4 | 59 | 33 | 57 | 56 | |
| 17 | 1 | 8 | 13 | 35 | 3 | 34 | 27 | 47 | 3 | 29 | 48 | 8 | 40 | 7 | 2 | |
| 18 | 2 | 36 | 56 | 44 | 10 | 43 | 32 | 48 | 4 | 58 | 31 | 17 | 48 | 16 | 7 | |
| 19 | 4 | 5 | 39 | 53 | 17 | 52 | 37 | 59 | 0 | 27 | 14 | 26 | 55 | 25 | 12 | |
| 20 | 5 | 34 | 23 | 2 | 25 | 1 | 43 | 50 | 1 | 55 | 57 | 36 | 2 | 34 | 17 | |
| 21 | 1 | 3 | 6 | 11 | 32 | 10 | 48 | 51 | 3 | 24 | 40 | 45 | 9 | 43 | 22 | |
| 22 | 2 | 31 | 49 | 20 | 39 | 19 | 53 | 52 | 4 | 53 | 23 | 54 | 17 | 52 | 27 | |
| 23 | 4 | 0 | 32 | 29 | 46 | 28 | 58 | 53 | 0 | 22 | 7 | 3 | 24 | 1 | 32 | |
| 24 | 5 | 29 | 15 | 38 | 54 | 38 | 3 | 54 | 1 | 50 | 50 | 12 | 31 | 10 | 38 | |
| 25 | 0 | 57 | 58 | 48 | 1 | 47 | 8 | 55 | 3 | 19 | 33 | 21 | 38 | 19 | 43 | |
| 26 | 2 | 26 | 41 | 57 | 8 | 56 | 13 | 56 | 4 | 48 | 16 | 30 | 46 | 28 | 48 | |
| 27 | 3 | 55 | 25 | 6 | 15 | 5 | 19 | 57 | 0 | 16 | 59 | 39 | 53 | 37 | 53 | |
| 28 | 5 | 24 | 8 | 15 | 23 | 14 | 24 | 58 | 1 | 45 | 42 | 49 | 0 | 46 | 58 | |
| 29 | 0 | 52 | 51 | 24 | 30 | 23 | 29 | 59 | 3 | 14 | 25 | 58 | 7 | 56 | 3 | |
| 30 | 2 | 21 | 34 | 33 | 37 | 32 | 34 | 60 | 4 | 43 | 9 | 7 | 15 | 5 | 9 | |
| Tage | Bewegung | Tage | Bewegung | |||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Sechzig | Grad | Min. | Secund. | Tertien | |||
| 1 | 0 | 13 | 3 | 53 | 56 | 31 | 6 | 45 | 0 | 52 | 11 | |
| 2 | 0 | 26 | 7 | 47 | 53 | 32 | 6 | 58 | 4 | 46 | 8 | |
| 3 | 0 | 39 | 11 | 41 | 49 | 33 | 7 | 11 | 8 | 40 | 4 | |
| 4 | 0 | 52 | 15 | 35 | 46 | 34 | 7 | 24 | 12 | 34 | 1 | |
| 5 | 1 | 5 | 19 | 29 | 42 | 35 | 7 | 37 | 16 | 27 | 57 | |
| 6 | 1 | 18 | 23 | 23 | 39 | 36 | 7 | 50 | 20 | 21 | 54 | |
| 7 | 1 | 31 | 27 | 17 | 35 | 37 | 8 | 3 | 24 | 15 | 50 | |
| 8 | 1 | 44 | 31 | 11 | 32 | 38 | 8 | 16 | 28 | 9 | 47 | |
| 9 | 1 | 57 | 35 | 5 | 28 | 39 | 8 | 29 | 32 | 3 | 43 | |
| 10 | 2 | 10 | 38 | 59 | 25 | 40 | 8 | 42 | 35 | 57 | 40 | |
| 11 | 2 | 23 | 42 | 53 | 21 | 41 | 8 | 55 | 39 | 51 | 36 | |
| 12 | 2 | 36 | 46 | 47 | 18 | 42 | 9 | 8 | 43 | 45 | 33 | |
| 13 | 2 | 49 | 50 | 41 | 14 | 43 | 9 | 21 | 47 | 39 | 29 | |
| 14 | 3 | 2 | 54 | 35 | 11 | 44 | 9 | 34 | 51 | 33 | 26 | |
| 15 | 3 | 15 | 58 | 29 | 7 | 45 | 9 | 47 | 55 | 27 | 22 | |
| 16 | 3 | 29 | 2 | 23 | 4 | 46 | 10 | 0 | 59 | 21 | 19 | |
| 17 | 3 | 42 | 6 | 17 | 0 | 47 | 10 | 14 | 3 | 15 | 15 | |
| 18 | 3 | 55 | 10 | 10 | 57 | 48 | 10 | 27 | 7 | 9 | 12 | |
| 19 | 4 | 8 | 14 | 4 | 53 | 49 | 10 | 40 | 11 | 3 | 8 | |
| 20 | 4 | 21 | 17 | 58 | 50 | 50 | 10 | 53 | 14 | 57 | 5 | |
| 21 | 4 | 34 | 21 | 52 | 46 | 51 | 11 | 6 | 18 | 51 | 1 | |
| 22 | 4 | 47 | 25 | 46 | 43 | 52 | 11 | 19 | 22 | 44 | 58 | |
| 23 | 5 | 0 | 29 | 40 | 39 | 53 | 11 | 32 | 26 | 38 | 54 | |
| 24 | 5 | 13 | 33 | 34 | 36 | 54 | 11 | 45 | 30 | 32 | 51 | |
| 25 | 5 | 26 | 37 | 28 | 32 | 55 | 11 | 58 | 34 | 26 | 47 | |
| 26 | 5 | 39 | 41 | 22 | 29 | 56 | 12 | 11 | 38 | 20 | 44 | |
| 27 | 5 | 52 | 45 | 16 | 25 | 57 | 12 | 24 | 42 | 14 | 40 | |
| 28 | 6 | 5 | 49 | 10 | 22 | 58 | 12 | 37 | 46 | 8 | 37 | |
| 29 | 6 | 18 | 53 | 4 | 18 | 59 | 12 | 50 | 50 | 2 | 33 | |
| 30 | 6 | 31 | 56 | 58 | 15 | 60 | 13 | 3 | 53 | 56 | 30 | |
| Aegyptische Jahre | Bewegung | Ort Christi 2. S. 9° 45′ Cap. 14. | Aegyptische Jahre | Bewegung | ||||||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | Sechzig | Grad | Min. | Secund. | Tertien | Manuscript | |||||
| Sec. | Tert. | Sec. | Tert. | |||||||||||||
| 1 | 2 | 28 | 42 | 45 | 17 | 44 | 31 | 31 | 4 | 50 | 5 | 23 | 57 | 0 | 4 | |
| 2 | 4 | 57 | 25 | 30 | 34 | 29 | 2 | 32 | 1 | 18 | 48 | 9 | 14 | 44 | 35 | |
| 3 | 1 | 26 | 8 | 15 | 52 | 13 | 33 | 33 | 3 | 47 | 30 | 54 | 32 | 29 | 6 | |
| 4 | 3 | 54 | 51 | 1 | 9 | 58 | 4 | 34 | 0 | 16 | 13 | 39 | 48 | 13 | 37 | |
| 5 | 0 | 23 | 33 | 46 | 26 | 42 | 35 | 35 | 2 | 44 | 56 | 25 | 6 | 58 | 8 | |
| 6 | 2 | 52 | 16 | 31 | 44 | 27 | 6 | 36 | 5 | 13 | 39 | 10 | 24 | 42 | 39 | |
| 7 | 5 | 20 | 59 | 17 | 1 | 11 | 37 | 37 | 1 | 42 | 21 | 55 | 41 | 27 | 10 | |
| 8 | 1 | 49 | 42 | 2 | 18 | 56 | 8 | 38 | 4 | 11 | 4 | 40 | 58 | 11 | 41 | |
| 9 | 4 | 18 | 24 | 47 | 36 | 40 | 39 | 39 | 0 | 39 | 47 | 26 | 16 | 56 | 12 | |
| 10 | 0 | 47 | 7 | 32 | 53 | 25 | 11 | 40 | 3 | 8 | 30 | 11 | 33 | 40 | 44 | |
| 11 | 3 | 15 | 50 | 18 | 10 | 9 | 42 | 41 | 5 | 37 | 12 | 56 | 50 | 25 | 15 | |
| 12 | 5 | 44 | 33 | 3 | 28 | 51 | 13 | 42 | 2 | 5 | 55 | 42 | 8 | 9 | 46 | |
| 13 | 2 | 13 | 15 | 48 | 45 | 38 | 44 | 43 | 4 | 34 | 38 | 27 | 25 | 54 | 17 | |
| 14 | 4 | 41 | 58 | 34 | 2 | 23 | 15 | 44 | 1 | 3 | 21 | 12 | 42 | 38 | 48 | |
| 15 | 1 | 10 | 41 | 19 | 20 | 7 | 46 | 45 | 3 | 32 | 3 | 58 | 0 | 23 | 19 | |
| 16 | 3 | 39 | 24 | 4 | 37 | 52 | 17 | 46 | 0 | 0 | 46 | 43 | 17 | 7 | 50 | |
| 17 | 0 | 8 | 6 | 49 | 54 | 36 | 48 | 47 | 2 | 29 | 29 | 28 | 34 | 57 | 21 | |
| 18 | 2 | 36 | 49 | 35 | 12 | 21 | 19 | 48 | 4 | 58 | 12 | 13 | 52 | 36 | 52 | |
| 19 | 5 | 5 | 32 | 20 | 29 | 5 | 50 | 49 | 1 | 26 | 54 | 59 | 8 | 21 | 23 | |
| 20 | 1 | 34 | 15 | 5 | 46 | 50 | 22 | 50 | 3 | 55 | 37 | 44 | 26 | 5 | 55 | |
| 21 | 4 | 2 | 57 | 51 | 4 | 34 | 53 | 51 | 0 | 24 | 29 | 29 | 44 | 50 | 26 | |
| 22 | 0 | 31 | 40 | 36 | 21 | 19 | 24 | 52 | 2 | 53 | 3 | 15 | 1 | 34 | 57 | |
| 23 | 3 | 0 | 23 | 21 | 38 | 3 | 55 | 53 | 5 | 21 | 46 | 0 | 18 | 19 | 28 | |
| 24 | 5 | 29 | 6 | 6 | 56 | 48 | 26 | 54 | 1 | 50 | 28 | 45 | 36 | 3 | 59 | |
| 25 | 1 | 57 | 48 | 52 | 13 | 32 | 57 | 55 | 4 | 19 | 11 | 30 | 53 | 18 | 30 | |
| 26 | 4 | 26 | 31 | 37 | 30 | 17 | 28 | 56 | 0 | 47 | 54 | 16 | 10 | 33 | 1 | |
| 27 | 0 | 55 | 14 | 22 | 48 | 1 | 59 | 57 | 3 | 16 | 37 | 1 | 28 | 17 | 32 | |
| 28 | 3 | 23 | 57 | 8 | 5 | 46 | 30 | 58 | 5 | 45 | 19 | 46 | 45 | 2 | 3 | |
| 29 | 5 | 52 | 39 | 53 | 22 | 31 | 1 | 59 | 2 | 14 | 2 | 32 | 2 | 46 | 34 | |
| 30 | 2 | 21 | 12 | 38 | 40 | 15 | 33 | 60 | 4 | 42 | 45 | 17 | 21 | 31 | 6 | |
| Tage | Bewegung | Tage | Bewegung | |||||||||
| Sechzig | Grad | Min. | Secund. | Tertien | Sechzig | Grad | Min. | Secund. | Tertien | |||
| 1 | 0 | 13 | 13 | 45 | 39 | 31 | 6 | 50 | 6 | 35 | 20 | |
| 2 | 0 | 26 | 27 | 31 | 18 | 32 | 7 | 3 | 20 | 20 | 59 | |
| 3 | 0 | 39 | 41 | 16 | 58 | 33 | 7 | 16 | 34 | 6 | 39 | |
| 4 | 0 | 52 | 55 | 2 | 37 | 34 | 7 | 29 | 47 | 52 | 18 | |
| 5 | 1 | 6 | 8 | 48 | 16 | 35 | 7 | 43 | 1 | 37 | 58 | |
| 6 | 1 | 19 | 22 | 33 | 56 | 36 | 7 | 56 | 15 | 23 | 37 | |
| 7 | 1 | 32 | 36 | 19 | 35 | 37 | 8 | 9 | 29 | 9 | 16 | |
| 8 | 1 | 45 | 50 | 5 | 14 | 38 | 8 | 22 | 42 | 54 | 56 | |
| 9 | 1 | 59 | 3 | 50 | 54 | 39 | 8 | 35 | 56 | 40 | 35 | |
| 10 | 2 | 12 | 17 | 36 | 33 | 40 | 8 | 49 | 10 | 26 | 14 | |
| 11 | 2 | 25 | 31 | 22 | 13 | 41 | 9 | 2 | 24 | 11 | 54 | |
| 12 | 2 | 38 | 45 | 7 | 52 | 42 | 9 | 15 | 37 | 57 | 33 | |
| 13 | 2 | 51 | 58 | 53 | 31 | 43 | 9 | 28 | 51 | 43 | 13 | |
| 14 | 3 | 5 | 12 | 39 | 11 | 44 | 9 | 42 | 5 | 28 | 52 | |
| 15 | 3 | 18 | 26 | 24 | 50 | 45 | 9 | 55 | 19 | 14 | 31 | |
| 16 | 3 | 31 | 40 | 10 | 29 | 46 | 10 | 8 | 33 | 0 | 11 | |
| 17 | 3 | 44 | 53 | 56 | 9 | 47 | 10 | 21 | 46 | 45 | 50 | |
| 18 | 3 | 58 | 7 | 41 | 48 | 48 | 10 | 35 | 0 | 31 | 29 | |
| 19 | 4 | 11 | 21 | 27 | 28 | 49 | 10 | 48 | 14 | 17 | 9 | |
| 20 | 4 | 24 | 35 | 13 | 7 | 50 | 11 | 1 | 28 | 2 | 48 | |
| 21 | 4 | 37 | 48 | 58 | 46 | 51 | 11 | 14 | 41 | 48 | 28 | |
| 22 | 4 | 51 | 2 | 44 | 26 | 52 | 11 | 27 | 55 | 34 | 7 | |
| 23 | 5 | 4 | 16 | 30 | 5 | 53 | 11 | 41 | 9 | 19 | 46 | |
| 24 | 5 | 17 | 30 | 15 | 44 | 54 | 11 | 54 | 23 | 5 | 26 | |
| 25 | 5 | 30 | 44 | 1 | 24 | 55 | 12 | 7 | 36 | 51 | 5 | |
| 26 | 5 | 43 | 57 | 47 | 3 | 56 | 12 | 20 | 50 | 36 | 44 | |
| 27 | 5 | 57 | 11 | 32 | 43 | 57 | 12 | 34 | 4 | 22 | 24 | |
| 28 | 6 | 10 | 25 | 18 | 22 | 58 | 12 | 47 | 18 | 8 | 3 | |
| 29 | 6 | 23 | 39 | 4 | 1 | 59 | 13 | 0 | 31 | 53 | 43 | |
| 30 | 6 | 36 | 25 | 49 | 41 | 60 | 13 | 13 | 45 | 39 | 22 | |
Soweit die gleichmässigen Bewegungen des Mondes bis jetzt sich erkennen lassen konnten, haben wir dieselben dargelegt. Nun müssen wir die Ungleichmässigkeit entwickeln, was wir durch die Methode des Epicykels thun wollen: und zwar zuerst bei derjenigen, welche beim Neu- und Vollmonde eintritt, und in Bezug auf welche die alten Mathematiker bei Discussion dreier Mondfinsternisse einen bewunderungswürdigen Scharfsinn entwickelt haben. Wir wollen den so von Jenen uns geebneten Weg verfolgen, und mit den von Ptolemäus sorgfältig beobachteten Finsternissen, drei andere mit nicht geringerer Sorgfalt aufgezeichnete vergleichen, um zu prüfen, ob die schon dargelegten gleichmässigen Bewegungen sich richtig so verhalten. Wir bedienen uns aber bei der Darstellung derselben, nach dem Beispiele der Alten, der mittleren Bewegungen der Sonne und des Mondes vom Orte der Frühlingsnachtgleiche, als gleichmässiger; da die Ungleichmässigkeit, welche wegen der ungleichmässigen Präcession der Nachtgleichen eintritt, in so kurzer Zeit, und wenn sie selbst zehn Jahre betrüge, nicht bemerkt wird. Ptolemäus[12] führt an, dass die erste Finsterniss nach ägyptischer Zeitrechnung im Jahre 17 des Kaisers Hadrian eintrat, nachdem der zwanzigste Payni verflossen war, das war das 133ste Jahr Christi den 6ten Mai[13]. Die Finsterniss war total, und die Zeit ihrer Mitte war drei viertel mittlere Stunden vor Mitternacht alexandrinischer Zeit; also nach der Zeit von Frauenburg oder Krakau[14] 1¾ Stunden vor der Mitternacht, welcher der 7te Mai folgte. Die Sonne stand 12° 15′ des Stiers[15], nach der mittleren Bewegung aber 12° 21′ des Stier’s[16]. Die zweite soll stattgefunden haben im Jahre 19 Hadrians, nach Ablauf zweier Tage des Monats Chöak, des vierten ägyptischen Monats, das war im Jahre Christi 134 October 20[17]. Die Finsterniss betrug fünf Sechstel des Durchmessers des Mondes von Norden, und die Zeit ihrer Mitte war eine mittlere Stunde vor Mitternacht alexandriner Zeit: also nach der Zeit von Krakau zwei Stunden vor Mitternacht[18]. Die Sonne stand in 25° 10′[WS 3] der Waage, nach der mittleren Bewegung aber in 26° 43′ der Waage[19]. Die dritte Finsterniss fand statt im Jahre 20 Hadrians nach Ablauf von 19 Tagen des Monats Pharmuthi, des achten ägyptischen Monats, oder nach Ablauf von 135 Jahren Christi und 6 Tagen des März[20]. Die Finsterniss betrug die Hälfte des Durchmessers wieder von Norden, und die Zeit ihrer Mitte war vier mittlere Stunden nach Mitternacht alexandriner Zeit; also nach der Zeit von Krakau 3 Stunden nach Mitternacht[21], am Morgen des 7ten März. Die Sonne stand in 14° 5′ der Fische, nach mittlerer Bewegung aber in 11° 44′ der Fische [22]. Es ergiebt sich also, dass der Mond in dem Zeitraum zwischen der ersten und zweiten Finsterniss so viel durchlaufen hatte, als die Sonne
[208] in ihrer scheinbaren Bewegung, nämlich, wenn wir die ganzen Umläufe weglassen, 161° 55′[23], und von der zweiten zur dritten 138° 55′[WS 3][24]. Es lagen aber in dem ersten Zeitraume 1 Jahr 166 Tage 23¾ Stunden scheinbare Sonnenzeit[25], also 235/8 Stunden mittlere Sonnen-Zeit[26]; im zweiten Zeitraum 1 Jahr 137 Tage 5 Stunden[27], also 5½ Stunden mittlere Sonnenzeit[28]. Es war die gemeinsame gleichmässige Bewegung von Sonne und Mond im ersten Zeitraume, wenn die ganzen Umläufe weggelassen werden, 169° 37′[29] und die Anomalie 110° 21′[30]; im zweiten Zeitraume die gleichmässige Bewegung von Sonne und Mond 137° 33′[31] und die Anomalie 81° 36′[32]. Es ergiebt sich also, dass in dem ersten Zeitraume 110° 21′ des Epicykels von der mittleren Bewegung des Mondes 7° 42′[33] abziehen, im zweiten 81° 36′[WS 3] des Epicykels zu der mittleren Bewegung des Mondes 1° 21′[34] addiren.
[209] und da er Aussenwinkel zu dem Dreiecke ist: so erhält man nach Abzug des Winkels den dritten als Rest zu 179° 15′. Es ergeben sich daraus die Seite gleich 199996, gleich 22120, wenn der Durchmesser des umschriebenen Kreises 200000 beträgt. Wenn aber gleich 147396 und gleich 26798: so ist gleich 16302. Da hierdurch wiederum in dem Dreiecke die beiden Seiten und gegeben sind, und der Peripheriewinkel dem Bogen von 81° 36′ angehört: so erhalten wir auch die dritte Seite nach den Sätzen über die ebenen Dreiecke zu 17960 eben jener Theile. Wenn aber der Durchmesser des Epicykels 200000 Theile betrüge: so wäre als Sehne von 81° 36′ gleich 130684 und die Uebrigen nach dem gegebenen Verhältnisse = 1072684 und = 118637 und der Bogen selbst = 72° 46′ 10″. Der Bogen betrug aber nach der Berechnung 168° 3′ folglich der Rest = 95° 16′ 50″, und dessen Sehne 147786. Hiernach beträgt die ganze Linie 1220470 derselben Theile. Da aber der Abschnitt kleiner als der Halbkreis ist, so liegt in demselben nicht der Mittelpunkt des Epicykels, sondern in dem Reste . Derselbe möge nun sein und durch beide Absiden möge die Linie gezogen werden, sei die grösste, die kleinste Abside. Nach dem 35sten Satze[35] des 3ten Buches von Euklid ist das Rechteck = . Da aber der Durchmesser des Kreises in halbirt ist, und in seiner gradlinigen Verlängerung liegt: so ist das Quadrat von um das Quadrat von grösser als das Rechteck [36]. Daraus ergiebt sich zu 1148556, wenn 100000 beträgt, und daraus folgt, dass der Radius des Epicykels gleich 8706, wenn gleich 100000. Nach diesen Feststellungen werde senkrecht gegen gezogen. Da nun das gegenseitige Verhältniss von , und in solchen Theilen gegeben ist, von denen 100000 enthält, und die Hälfte von ist: so beträgt 73893, und die Ganze den 1146577. Nun sind aber in dem Dreiecke die beiden Seiten und gegeben und der Winkel ein Rechter. Es beträgt also der Centriwinkel 86° 38½′, und so viel beträgt auch der Bogen , und als Rest vom Halbkreise der Bogen 93° 21½′, davon der Bogen als die Hälfte des Bogens = 47° 38½′ abgezogen, giebt als Rest = 45° 43′, und dies ist der Abstand des Mondes von der grössten Abside im Epicykel bei der ersten Finsterniss, oder die Anomalie. Der ganze Bogen betrug aber 110° 21′, folglich beträgt der Rest , als Anomalie bei der zweiten Finsterniss 64° 38′, und der ganze Bogen , bei welchem die dritte Finsterniss eintrat, 146° 14′. Nun ist auch klar, dass, da der Winkel = 86° 38½′ ist, wobei 360° = 4 Rechten, — der Winkel , als Rest von einem Rechten, 3° 21½′ beträgt; und dies ist die Prosthaphärese, welche die Anomalie bei der ersten Finsterniss hinzuaddirt. Der ganze Winkel betrug aber 7° 42′, der Rest also 4° 20½′, und diese werden bei der zweiten Finsterniss von der gleichmässigen Bewegung des Mondes auf dem Bogen , abgezogen. Und da der Winkel 1° 21′ betrug: so bleibt als Rest = 2° 59′ 30″, als die bei der dritten Finsterniss [210] wegen des Bogens abzuziehende Prohthaphärese. Es war also der mittlere Ort des Mondes, d. h. der Mittelpunkt bei der ersten Finsterniss in 9° 53′ des Skorpions, weil sein scheinbarer Ort in 13° 15′ des Skorpions lag, nämlich so viel als die Sonne in dem diametral gegenüberliegenden Punkte des Stiers einnahm. Und ebenso war der mittlere Ort des Mondes bei der zweiten Finsterniss in 29½° des Widders. Bei der dritten in 17° 4′ der Jungfrau. Die mittleren Abstände des Mondes von der Sonne waren bei der ersten Finsterniss 177° 33′, bei der zweiten 182° 47′, bei der letzten 185° 20′[37]. In dieser Weise Ptolomäus. Seinem Beispiele folgend, gehen wir nun zu einer andern Dreizahl von Mondfinsternissen über, welche von uns ebenfalls sehr sorgfältig beobachtet worden sind. Die erste ereignete sich im Jahre Christi 1511 nach Ablauf von 6 Tagen des Monats October. Der Mond begann sich zu verfinstern 1⅛ Stunden mittlere Zeit vor Mitternacht, und war wieder ganz hell 2⅓ Stunden nach Mitternacht. Die Mitte der Verfinsterung war also ½ + 1/12 Stunden nach Mitternacht, am Morgen des 7ten Octobers. Der Mond wurde total verfinstert[WS 6], während die Sonne in 22° 25′ der Waage stand, aber ihr mittlerer Ort war in 24° 13′ der Waage. Die zweite ebenfalls totale Finsterniss haben wir notirt im Jahre Christi 1522 im Monat September, nachdem 5 Tage desselben verstrichen waren; der Anfang war ⅖ mittlere Stunden vor Mitternacht, ihre Mitte aber 1⅓ Stunden nach Mitternacht, welcher der 6te September folgte. Die Sonne stand in 22⅕° der Jungfrau, ihr mittlerer Ort war aber in 23° 59′ der Jungfrau. Die dritte war im Jahre Christi 1523 nach Ablauf von 25 Tagen des Monats August und begann 2⅘ Stunden nach Mitternacht, und die Mitte dieser ebenfalls totalen Finsterniss war 45/12 Stunden nach Mitternacht, also schon am 26sten August, wo die Sonne in 11° 21′ der Jungfrau, nach mittlerer Bewegung aber in 13° 2′ der Jungfrau stand. Hieraus ist klar, dass der Unterschied der wahren Oerter der Sonne und des Mondes bei der ersten und zweiten Finsterniss 329° 47′, bei der zweiten und dritten aber 349° 9′ betrug. Die Zwischenzeit zwischen der ersten und zweiten Finsterniss war 10 ägyptische Jahre 337 Tage und 45 Minuten, nach scheinbarer Zeit, nach der genauen Gleichmässigkeit aber waren es 48 Minuten. Zwischen der zweiten und dritten lagen 354 Tage 3 Stunden 5 Minuten, aber nach gleichmässiger Zeit 3 Stunden 9 Minuten. Im ersten Zeitraume beträgt die mittlere Bewegung der Sonne und des Mondes zusammengenommen und mit Weglassung der ganzen Kreise 334° 47′[38], die der Anomalie 250° 36′[39], und das von der gleichmässigen Bewegung Abzuziehende ungefähr 5°[40]. Im zweiten Zeitraume beträgt die mittlere Bewegung der Sonne und des Mondes 346° 10′, die der Anomalie 306° 43′, und das zu der gleichmässigen Bewegung zu addirende 2° 59′. Nun sei der Epicykel, und der Ort des Mondes bei der Mitte der ersten Finsterniss, bei der zweiten, bei der dritten. Die Bewegung des Epicykels gehe von nach und von nach , d. h. oben rückläufig, unten rechtläufig. Der Bogen betrage 250° 36′, durch welchen von der mittleren
[211] Bewegung des Mondes, wie gesagt, in dem ersten Zeitraume 5° abgezogen werden.

[213]
Aus dem, was an den Monfinsternissen entwickelt ist, lässt sich auch beurtheilen, ob es mit den gleichmässigen Bewegungen des Mondes, welche wir früher entwickelt haben, seine Richtigkeit hat. Es ist nämlich gezeigt, dass bei der zweiten der ersten Finsternisse der Abstand des Mondes von der Sonne 182° 47′[43], die Anomalie 64° 38′ betrug. Bei der zweiten der späteren Finsternisse aus unserer Zeit war der Abstand des Mondes von der Sonne 182° 51′, und die Anomalie 74° 27′. Es liegen aber in der Zwischenzeit 17166 volle Monate und überdies 4′, und die Bewegung der Anomalie beträgt mit Weglassung der ganzen Kreise 9° 49′. Die Zeit aber, welche verstrich vom 19ten Jahre Hadrians, den zweiten Chöak 2 Stunden vor Mitternacht, welcher der 3te Tag desselben Monats folgte, bis zum Jahre Christi 1522 den 5ten September 1⅓ Uhr wahre Zeit, beträgt, wenn Alles auf mittlere Zeit reducirt ist, 1388 ägyptische Jahre 302 Tage 3⅓ Stunden, was auf mittlere Zeit reducirt 3h 34m nach Mitternacht giebt.[44] Und in dieser Zeit wäre die Bewegung des Mondes ausser 17165 voller Umläufe oder gleicher Monate, nach Hipparch und Ptolomäus gewesen 359° 38′[45]. Bei der Anomalie aber nach Hipparch 9° 37′, nach Ptolomäus dagegen 9° 11′[46]. Es fehlen also der Bewegung des Mondes seit jenen Beiden 26′[47], der Anomalie 38′[48], welche bei den unsrigen hinzukommen, und dies stimmt mit den Zahlen, welche wir entwickelt haben.
Nunmehr müssen auch hier, wie früher, die Oerter oder die bestimmten Anfangspunkte für die Jahre der Olympiaden, Alexanders, Cäsars, Christi und wenn sonst noch welche zu wünschen wären, festgestellt werden. Wenn wir zu dem Ende die zweite von den dreien alten Finsternissen berücksichtigen, welche im 19ten Jahre Hadrians, am 2ten Chöak der Aegypter eine Stunde vor Mitternacht zu Alexandrien, für uns aber unter dem Meridian von Krakau zwei Stunden vor Mitternacht sich zugetragen hat: so finden wir vom Anfange der Jahre Christi bis zu diesem Augenblicke 133 ägyptische Jahre 325 Tage 22 Stunden, genauer aber 21 Stunden 37 Minuten. In dieser Zeit ist die Bewegung des Mondes nach unserer Berechnung 332° 49′[49], die der Anomalie 217° 30′[50]. Wenn man diese Grössen beziehlich von denjenigen abzieht, welche bei der Finsterniss gefunden sind: so bleibt als mittlerer Ort des Mondes von der Sonne 209° 58′[51] und für die Anomalie 207° 7′[52] für den Anfang der Jahre Christi um Mitternacht den 1sten Januar. Nun sind es wieder bis zum Anfange der Jahre Christi 193 [214] Olympiaden 2 Jahre und 184½[53] Tage, welche 775 ägyptische Jahre 12½ Tage oder genauer 12 Stunden 11 Minuten ausmachen. Ebenso rechnet man vom Tode Alexanders bis Christi Geburt 323 Jahre ägyptisch 130½ Tage[54] wahre Zeit, genau aber 12h 16m. Und von Cäsar bis Christus sind es 45 ägyptische Jahre und 12 Tage, bei welchen Beiden die mittlere mit den wahren Zeiten übereinstimmen. Wenn wir also die Bewegungen, welche diesen Zeitdifferenzen entsprechen, von den Oertern Christi abziehen: so erhalten wir für den Mittag des ersten Hekatombäon der ersten Olympiade als mittleren Abstand des Mondes von der Sonne 39° 48′[55] und als Anomalie 46° 20′[56]. Für den Mittag des ersten Thoth der Jahre Alexanders: Mond von der Sonne 310° 44′[57], Anomalie 85° 41′[58]. Für Mitternacht des ersten Januars der Jahre Cäsars: Mond von der Sonne 350° 39′[59], Anomalie 17° 58′[60]. Alles dieses gilt für den Meridian von Krakau, da Frauenburg, wo wir meistens unsere Beobachtungen gemacht haben, an der Mündung der Baude gelegen, diesem Meridiane angehört, wie uns die an beiden Orten zugleich beobachteten Sonnen- und Mondfinsternisse gelehrt haben; unter diesem Meridian liegt auch das macedonische Dyrrhachium, welches vor Alters Epidamnum hiess[61].
So ist also die gleichmässige Bewegung des Mondes, nebst ihrer ersten Ungleichmässigkeit entwickelt. Nunmehr haben wir zu untersuchen, in welchem Verhältniss der erste Epicykel zu dem zweiten, und jeder von Beiden zu der Entfernung von dem Mittelpunkte der Erde steht. Es findet sich aber, wie gesagt, die grösste Ungleichmässigkeit in den mittleren Quadraturen, wenn der zunehmende oder abnehmende Mond halb ist, und sie dehnt sich auf 7⅔° aus, wie das auch die Alten angemerkt haben[62]. Sie beobachteten nämlich die Zeit, zu welcher das Mondviertel nahe mit der mittleren Entfernung des Epicykels zusammentraf, und zwar in der Gegend des Berührungspunktes mit der vom Mittelpunkte der Erde gezogenen geraden Linie. Diese Zeit konnte durch die oben entwickelte Berechnung leicht ermittelt werden. Da nun zu dieser Zeit der Mond in der Gegend des 90sten Grades der Ekliptik, von Osten nach Westen gerechnet, steht: so vermieden sie den Fehler, welchen die Parallaxe für die Länge herbeiführen konnte. Denn alsdann schneidet der Vertikalkreis die Ekliptik rechtwinklig, und lässt keine Aenderung der Länge zu, sondern die ganze Aenderung fällt auf die Breite. Nun massen sie mit Hülfe des Astrolabiums den Ort des Mondes bezogen auf die Sonne, und fanden bei angestellter Vergleichung, wie gesagt, den Mond um 7° 40′ anstatt um 5° abweichend von dem mittleren Orte. Man construire den Epicykel , sein Mittelpunkt sei ; von
[215]
Aus dieser Ableitung lässt sich auch erkennen, wie der Mond in seinem ersten Epicykel sich ungleichmässig bewegt, wobei die grösste Differenz dann eintritt, wenn er sichelförmig oder höckerig oder auch halbvoll ist. Es sei wiederum jener erste Epicykel, welchen der Mittelpunkt des zweiten Epicykels beschreibt; sein Mittelpunkt , die grösste Abside , die kleinste . Irgendwo in der Peripherie werde der Punkt angenommen, und gezogen. Es verhalte sich aber zu wie 1097 zu 237. Um den Mittelpunkt werde mit dem Radius der zweite Epicykel beschrieben, und die beiden Tangenten und gezogen. Die Bewegung des kleinen Epicykels gehe von nach vor sich, d. h. oben rückläufig. Der Mond aber bewege sich von nach ebenfalls rückläufig. Es ergiebt sich also, dass, während die Bewegung gleichmässig ist, der zweite Epicykel, durch seine Bewegung eben jene Gleichmässigkeit um den Bogen vergrössert, und durch vermindert. Nun ist aber in dem Dreiecke , der Winkel bei ein rechter, und enthält 237 solcher Theile, von denen auf 1097
[216]
Nachdem dies Alles so vorausgeschickt ist, wollen wir nun zeigen, wie aus jenen gegebenen gleichmässigen Bewegungen des Mondes die erscheinende und gleichmässige Bewegung auf dem Wege der Construction abgeleitet wird; indem wir ein Beispiel aus den Beobachtungen des Hipparch nehmen, an welchem die Ableitung zugleich durch den Versuch bewiesen wird. Im Jahre 197 nach Alexanders Tode also, am 17ten Pauni, des zehnten ägyptischen Monats, nach Ablauf von 9⅓ Tagesstunden, fand Hipparch[64] in Rhodos bei der Beobachtung der Sonne und des Mondes mittelst des Astrolabiums, dass sie um 48⅒° von einander abstanden, und der Mond der Sonne um so viel nachfolgte. Da er nun den Ort der Sonne auf 11° weniger ⅒° des Krebses[65] bestimmte: so folgte, dass der Mond in 29° des Löwen[66] stand. Um dieselbe Zeit ging der 29ste Grad des Skorpions auf, während der 10te Grad der Jungfrau durch den Meridian von Rhodos ging, und der Nordpol 36° Höhe hatte[67]. Hienaus ergiebt sich, dass der Mond, welcher damals um 90° in der Ekliptik von dem Horizonte entfernt war, keine oder wenigstens eine unmerkliche Parallaxe in der Länge erlitt. Da aber diese Beobachtung an jenem siebenzehnten Tage 3⅓ Stunden, welchen für Rhodos 4 Aequinoctialstunden entsprechen[68], Nachmittags angestellt wurde[69], so waren diese für Krakau 3⅙ Aequinoctialstunden, weil Rhodos um ⅙ Stunde uns näher liegt als Alexandrien. Es waren also seit Alexanders Tode 196 Jahre 286 Tage 3 Stunden 10 Minuten nach einfacher Rechnung; genau aber 3 Stunden 20 Minuten verflossen. In dieser Zeit kam die Sonne in mittlerer
[217]
[218] des natürlichen Tages auseinandergesetzt haben. Ebenso finden wir auch, wenn wir die Berechnung auf die Mondbahn, von der Ptolomäus gelehrt hat, dass sie gegen die Ekliptik geneigt sei, übertragen: dass der Unterschied der Länge für jene Oerter in Bezug auf die Ekliptik 7′ beträgt, welcher Unterschied verdoppelt zu 14 Minuten wird, und so in entsprechendem Wachsen und Abnehmen auftritt. Stehen also Sonne und Mond um einen Viertelkreis auseinander, und befindet sich die nördliche und südliche Grenze der Breite in der Mitte zwischen denselben: so ist der eingeschlossene Bogen der Ekliptik um 14 Minuten grösser als der Quadrant der Mondbahn, und die Kreise durch die Pole der Ekliptik schliessen in den übrigen Quadranten, welche durch die Knoten halbirt werden, ebenso viel weniger als der Quadrant ein; und so auch hier. Da der Mond etwa in der Mitte zwischen der südlichen Grenze und dem aufsteigenden Knoten, welchen die Neueren den Drachenkopf nennen, stand; und die Sonne schon an dem andern, absteigenden Knoten, welchen Jene den Schwanz nennen, vorüber war: so kann es nicht befremden, wenn jene Monddistanz von 47° 57′ in seiner schiefen Bahn, auf die Ekliptik reducirt, sich vergrösserte um wenigstens 7′; abgesehen davon, dass auch die Sonne bei ihrem Untergange die Erscheinung etwas verkleinerte, worüber bei der Entwickelung der Parallaxen deutlicher gehandelt werden soll. So stimmt jene Monddistanz, welche Hipparch durch sein Instrument auf 48° 6′ bestimmt hat, in bewunderungswürdiger Weise, wie nach einer Verabredung, mit unserer Berechnung überein.
An diesem Beispiele, glaube ich, kann die Methode, die Mondbewegungen zu berechnen, im Allgemeinen eingesehen werden. Die beiden Seiten und des Dreiecks bleiben immer dieselben; nach dem Winkel , welcher sich fortwährend ändert, aber doch immer gegeben ist, berechnen wir die dritte Seite nebst dem Winkel , welcher die Prosthaphärese zur Ausgleichung der Anomalie liefert. Wenn ferner in dem Dreiecke die beiden Seiten und nebst dem Winkel in Zahlen gegeben sind: so ergiebt sich in derselben Weise der Winkel zwischen der gleichmässigen und der wahren Bewegung am Mittelpunkt der Erde. Um dies noch zu erleichtern, wollen wir ein Verzeichniss dieser Prosthaphäresen aufstellen, welches sechs Spalten enthält. Auf die beiden gemeinsamen Zahlenangaben des Kreises folgen in dritter Reihe die Prosthaphäresen, welche von dem kleinen Epicykel herrührend, in zweimonatlicher Bewegung, die Gleichmässigkeit der ersten Anomalie ändern. Die darauf folgende Spalte bleibt noch leer und künftigen Zahlen vorbehalten. Die fünfte Spalte nehmen wir zu den Prosthaphäresen des ersten und grösseren Epicykels, welche in den
[219]
| Gemeinschaftliche Zahlen | Prostaphäresen des kleinen Epicykels | Proportional-Minuten | Prostaphäresen des grossen Epicykels | Abweichung | Nördliche Breite | |||||
| Grade | Grade | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | |
| 3 | 357 | 0 | 51 | 0 | 0 | 14 | 0 | 7 | 4 | 59 |
| 6 | 354 | 1 | 40 | 0 | 0 | 28 | 0 | 14 | 4 | 58 |
| 9 | 351 | 2 | 28 | 1 | 0 | 43 | 0 | 21 | 4 | 56 |
| 12 | 348 | 3 | 15 | 1 | 0 | 57 | 0 | 28 | 4 | 53 |
| 15 | 345 | 4 | 1 | 2 | 1 | 11 | 0 | 35 | 4 | 50 |
| 18 | 342 | 4 | 47 | 3 | 1 | 24 | 0 | 43 | 4 | 45 |
| 21 | 339 | 5 | 31 | 3 | 1 | 38 | 0 | 50 | 4 | 40 |
| 24 | 336 | 6 | 13 | 4 | 1 | 51 | 0 | 56 | 4 | 34 |
| 27 | 333 | 6 | 54 | 5 | 2 | 5 | 1 | 4 | 4 | 27 |
| 30 | 330 | 7 | 34 | 5 | 2 | 17 | 1 | 12 | 4 | 20 |
| 33 | 327 | 8 | 10 | 6 | 2 | 30 | 1 | 18 | 4 | 12 |
| 36 | 324 | 8 | 44 | 7 | 2 | 42 | 1 | 25 | 4 | 3 |
| 39 | 321 | 9 | 16 | 8 | 2 | 54 | 1 | 30 | 3 | 53 |
| 42 | 318 | 9 | 47 | 10 | 3 | 6 | 1 | 37 | 3 | 43 |
| 45 | 315 | 10 | 14 | 11 | 3 | 17 | 1 | 42 | 3 | 32 |
| 48 | 312 | 10 | 30 | 12 | 3 | 27 | 1 | 48 | 3 | 20 |
| 51 | 309 | 11 | 0 | 13 | 3 | 38 | 1 | 52 | 3 | 8 |
| 54 | 306 | 11 | 21 | 15 | 3 | 47 | 1 | 57 | 2 | 56 |
| 57 | 303 | 11 | 38 | 16 | 3 | 56 | 2 | 2 | 2 | 44 |
| 60 | 300 | 11 | 50 | 18 | 4 | 5 | 2 | 6 | 2 | 30 |
| 63 | 297 | 12 | 2 | 19 | 4 | 13 | 2 | 10 | 2 | 16 |
| 66 | 294 | 12 | 12 | 21 | 4 | 20 | 2 | 15 | 2 | 2 |
| 69 | 291 | 12 | 18 | 22 | 4 | 27 | 2 | 18 | 1 | 47 |
| 72 | 288 | 12 | 23 | 24 | 4 | 33 | 2 | 21 | 1 | 33 |
| 75 | 285 | 12 | 27 | 25 | 4 | 39 | 2 | 25 | 1 | 18 |
| 78 | 282 | 12 | 28 | 27 | 4 | 43 | 2 | 28 | 1 | 2 |
| 81 | 279 | 12 | 26 | 28 | 4 | 47 | 2 | 30 | 0 | 47 |
| 84 | 276 | 12 | 23 | 30 | 4 | 51 | 2 | 34 | 0 | 31 |
| 87 | 273 | 12 | 17 | 32 | 4 | 53 | 2 | 37 | 0 | 16 |
| 90 | 270 | 12 | 12 | 34 | 4 | 55 | 2 | 40 | 0 | 0 |
| Gemeinschaftliche Zahlen | Prostaphäresen des kleinen Epicykels | Proportional-Minuten | Prostaphäresen des grossen Epicykels | Abweichung | Südliche Breite[76] | |||||
| Grade | Grade | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | |
| 93 | 267 | 12 | 3 | 35 | 4 | 56 | 2 | 42 | 0 | 16 |
| 96 | 264 | 11 | 53 | 37 | 4 | 56 | 2 | 42 | 0 | 31 |
| 99 | 261 | 11 | 41 | 38 | 4 | 55 | 2 | 43 | 0 | 47 |
| 102 | 258 | 11 | 27 | 39 | 4 | 54 | 2 | 43 | 1 | 2 |
| 105 | 255 | 11 | 10 | 41 | 4 | 51 | 2 | 44 | 1 | 18 |
| 108 | 252 | 10 | 52 | 42 | 4 | 48 | 2 | 44 | 1 | 33 |
| 111 | 249 | 10 | 35 | 43 | 4 | 44 | 2 | 43 | 1 | 47 |
| 114 | 246 | 10 | 17 | 45 | 4 | 39 | 2 | 41 | 2 | 2 |
| 117 | 243 | 9 | 57 | 46 | 4 | 34 | 2 | 38 | 2 | 16 |
| 120 | 240 | 9 | 35 | 47 | 4 | 27 | 2 | 35 | 2 | 30 |
| 123 | 237 | 9 | 13 | 48 | 4 | 20 | 2 | 31 | 2 | 44 |
| 126 | 234 | 8 | 50 | 49 | 4 | 11 | 2 | 27 | 2 | 56 |
| 129 | 231 | 8 | 25 | 50 | 4 | 2 | 2 | 22 | 3 | 9 |
| 132 | 228 | 7 | 59 | 51 | 3 | 53 | 2 | 18 | 3 | 21 |
| 135 | 225 | 7 | 33 | 52 | 3 | 42 | 2 | 13 | 3 | 32 |
| 138 | 222 | 7 | 7 | 53 | 3 | 31 | 2 | 8 | 3 | 43 |
| 141 | 219 | 6 | 38 | 54 | 3 | 19 | 2 | 1 | 3 | 53 |
| 144 | 216 | 6 | 9 | 55 | 3 | 7 | 1 | 53 | 4 | 3 |
| 147 | 213 | 5 | 40 | 56 | 2 | 53 | 1 | 46 | 4 | 12 |
| 150 | 210 | 5 | 11 | 57 | 2 | 40 | 1 | 37 | 4 | 20 |
| 153 | 207 | 4 | 42 | 57 | 2 | 25 | 1 | 28 | 4 | 27 |
| 156 | 204 | 4 | 11 | 58 | 2 | 10 | 1 | 20 | 4 | 34 |
| 159 | 201 | 3 | 41 | 58 | 1 | 55 | 1 | 12 | 4 | 40 |
| 162 | 198 | 3 | 10 | 59 | 1 | 39 | 1 | 4 | 4 | 45 |
| 165 | 195 | 2 | 39 | 59 | 1 | 23 | 0 | 53 | 4 | 50 |
| 168 | 192 | 2 | 7 | 59 | 1 | 7 | 0 | 43 | 4 | 53 |
| 171 | 189 | 1 | 36 | 60 | 0 | 51 | 0 | 33 | 4 | 56 |
| 174 | 186 | 1 | 4 | 60 | 0 | 34 | 0 | 22 | 4 | 58 |
| 177 | 183 | 0 | 32 | 60 | 0 | 17 | 0 | 11 | 4 | 59 |
| 180 | 180 | 0 | 0 | 60 | 0 | 0 | 0 | 0 | 5 | 0 |
Die Methode, nach welcher die erscheinende Mondbewegung berechnet wird, ergiebt sich aus dem Dargelegten, und ist folgende. Die gegebene Zeit, für welche wir den Ort des Mondes suchen, reduciren wir auf die gleichmässige; durch diese leiten wir die mittleren Bewegungen der Länge, Anomalie und Breite, welche Letztere wir auch bald bestimmen wollen, in derselben Weise her, wie wir es bei der Sonne gethan haben, von dem gegebenen Anfange Christi oder einem andern an gerechnet; und stellen die Oerter der einzelnen Bestimmungen für die gegebene Zeit fest. Darauf suchen wir die gleichmässige Länge des Mondes, oder seine doppelte Distanz von der Sonne in der Tafel, und notiren die in der dritten Spalte danebenstehende Prosthaphärese nebst den darauf folgenden Proportionaltheilen. Wenn nun die Zahl, mit welcher wir in die Tafel eingegangen sind, in der ersten Spalte steht oder kleiner als 180° ist: so addiren wir die Prosthaphärese zu der Mond-Anomalie, wenn sie aber grösser als 180° ist, und in der zweiten Spalte steht, so ziehen wir sie davon ab, und erhalten die ausgeglichene Anomalie des Mondes, als seine wahre Distanz von der grössten Abside, mit welcher wir wieder in die Tafel eingehen, und die entsprechende Prosthaphärese der fünften Spalte, nebst der Abweichung, welche in der sechsten Spalte folgt, entnehmen; diese Abweichung vergrössert der zweite Epicykel an dem ersten; der hierzu gehörende Proportionaltheil wird nach dem Verhältniss der gefundenen Proportionaltheile zu 60 berechnet, und immer zu dieser Prosthaphärese addirt. Diese Summe wird von der mittleren Bewegung der Länge und Breite abgezogen, so lange die ausgeglichene Anomalie kleiner als 180° oder als der Halbkreis ist: und addirt, wenn die Anomalie grösser ist. Auf diese Weise erhalten wir den wahren Abstand des Mondes von dem mittleren Orte der Sonne, und die ausgeglichene Bewegung der Breite. Daraus ist denn auch der wahre Ort des Mondes, sowohl vom ersten Sterne des Widders durch die einfache Bewegung der Sonne, als auch vom Frühlingsnachtgleichenpunkte durch die zusammengesetzte, nämlich durch die wegen der Präcession desselben corrigirte. Durch die ausgeglichene Bewegung der Breite endlich erhalten wir aus der siebenten und letzten Spalte des Verzeichnisses die Grade der Breite, um welche der Mond von der Ekliptik absteht. Diese Breite wird aber dann nördlich sein, wenn die Bewegung der Länge[77] auf der ersten Seite der Tafel steht, d. h. wenn sie kleiner als 90° oder grösser als 270° ist; sonst ergiebt sich eine südliche Breite. Und demnach steigt der Mond von Norden herab bis 180°, und erhebt sich von jener südlichen Grenze, bis er die andere Hälfte des Kreises durchlaufen hat. Auf diese Weise hat der erscheinende Mondlauf gewissermaassen ebensoviel um den Mittelpunkt der Erde auszuführen, als der Mittelpunkt der Erde um die Sonne.
[223]Nun muss auch die Berechnung der Bewegung der Mondbreite entwickelt werden, welche deswegen schwieriger zu finden zu sein scheint, weil sie von mehr Umständen abhängt. Denn, wie wir oben gesagt haben, wenn zwei Mondfinsternisse in Allem ähnlich und gleich sind, d. h. wenn die verdunkelten Theile dieselben nördlichen oder südlichen Lagen haben, und an demselben aufsteigenden oder absteigenden Knoten stattfinden, und auch die Entfernung des Mondes von der Erde und von der grössten Abside dieselbe ist: so lässt sich wohl erkennen, dass der Mond, bei Eintritt jener Uebereinstimmung, in seiner wahren Bewegung ganze Umläufe seiner Breite zurückgelegt hat; und da der Schatten der Erde ein Kegel ist, und — wenn ein grader Kegel durch eine mit der Basis parallele Ebene geschnitten wird — der Schnittkreis kleiner in grösserer, grösser in kleinerer und folglich gleich in gleicher Entfernung von der Basis ist: so wird auch der Mond in gleichen Entfernungen von der Erde gleiche Schattenkreise passiren und uns bei den Beobachtungen gleiche Scheiben seiner selbst darbieten. Hieraus folgt, dass der Mond, wenn er an derselben Stelle und in gleicher Entfernung von dem Mittelpunkte des Schattens um gleiche Theile hervorragt, uns seiner gleichen Breite versichert, woraus geschlossen werden muss, dass er, an den früheren Ort der Breite zurückgekehrt, von demselben Punkte der Ekliptik um gleiche Bogen abstehe; — namentlich wenn auch der Ort für beide Körper übereinstimmt: — denn sowohl sein eigenes Nähern und Entfernen, als auch dasjenige der Erde ändert die ganze Grösse des Schattens, und zwar in einem Maasse, welches kaum ermittelt werden kann. Jemehr also die Zeit für beide übereinstimmt, desto bestimmter können wir die Bewegung der Mondbreite erhalten, wie das schon bei der Sonne erwähnt ist. Da es aber selten vorkommt, dass man zwei in diesen Beziehungen übereinstimmende Finsternisse findet, — uns sind wenigstens bis heute keine solche begegnet, — so wollen wir zeigen, dass es auch einen andern Weg giebt, auf welchem man dasselbe erreichen kann. Wenn nämlich der Mond, während die übrigen Bedingungen bleiben, auf entgegengesetzten Seiten, und an entgegengesetzten Knoten verfinstert wird: so beweist dies, dass der Mond bei der zweiten Finsterniss an einen dem früheren diametral entgegengesetzten Ort gelangt ist, und ausser ganzen Umläufen, einen Halbkreis beschrieben hat. Dies scheint zur Untersuchung dieses Gegenstandes auszureichen. Wir haben nämlich zwei Finsternisse gefunden, welche diesen Bedingungen nahe kommen: die Erste, im 7ten Jahre des Ptolomäus Philometor, welches das 150ste Alexanders war, nachdem, wie Claudius[78] sagt, 27 Tage des siebenten ägyptischen Monats Phamenoth verstrichen war, in der Nacht, auf welche der 28ste folgte. Der Mond wurde vom Anfange der 8ten Stunde bis zum Ende der 10ten Stunde in nächtlichen Zeitstunden Alexandriens, im Maximum um 7 Zoll des Monddurchmessers von Norden [224] her bei absteigendem Knoten verfinstert. Die Mitte der Verfinsterungszeit war zwei Zeitstunden (wie er sagt) nach Mitternacht, welche 2⅓ Aequinoctialstunden ausmachen, während die Sonne im sechsten Grade des Stiers stand, in Krakau wäre es eine und ⅓ Stunde gewesen. Die Zweite haben wir unter dem Meridiane von Krakau im Jahre Christi 1509 den 2ten Juni, als die Sonne im 21sten Grade der Zwillinge stand, beobachtet; ihre Mitte fiel 11⅗ Aequinoctialstunden nach dem Mittage jenes Tages, wobei ungefähr 8 Zoll des Monddurchmessers von Süden her beim aufsteigenden Knoten verfinstert wurden. Es sind also vom Anfange der Jahre Alexanders 149 ägyptische Jahre 206 Tage 14⅓ Stunden Alexandriner Zeit, aber 13⅓ Stunden scheinbare Krakauer Zeit, genau 13½ Stunden. Zu dieser Zeit war der Ort der gleichmässigen Anomalie nach unserer Rechnung 163° 33′, was mit Ptolomäus[79] ungefähr stimmt, und die Prosthaphärese betrug 1° 23′, um welche der wahre Ort des Mondes kleiner war, als der gleichmässige. Für die zweite Finsterniss waren es aber seit demselben Anfange der Jahre Alexanders 1832 ägyptische Jahre 295 Tage 11 Stunden 45 Minuten scheinbare Zeit, gleichmässige aber 11 Stunden 55 Minuten. Daher betrug die gleichmässige Bewegung des Mondes 182° 18′, der Ort der Anomalie 159° 55′, die ausgeglichene aber 159° 13′, die Prosthaphärese, um welche die gleichmässige Bewegung kleiner war, als die scheinbare, 1° 44′. Es ergiebt sich also, dass bei beiden Finsternissen die Entfernung des Mondes von der Erde gleich, und die Sonne bei beiden im Apogeum gewesen ist; aber in der Verfinsterung bestand ein Unterschied von einem Zoll. Da aber der Durchmesser des Mondes ungefähr einen halben Grad einzunehmen pflegt, wie wir später beweisen werden: so beträgt sein zwölfter Theil, für einen Zoll, 2½ Minuten, denen für den schiefen Kreis des Mondes in der Nähe des Knoten fast ein halber Grad entspricht, um welchen bei der zweiten Finsterniss der Mond von dem aufsteigenden Knoten mehr entfernt war, als bei der ersten von dem absteigenden Knoten, woraus klar ist, dass die wahre Bewegung der Mondbreite ausser den vollen Umläufen 179½° betragen hat. Aber zu der gleichmässigen Anomalie des Mondes zwischen der ersten und zweiten Finsterniss kommen 21 Minuten hinzu, um welche die Prosthaphäresen unter sich verschieden sind. Wir haben also die gleichmässige Bewegung der Mondbreite ausser den ganzen Umläufen = 179° 51′. Die Zeit zwischen beiden Finsternissen betrug 1683 ägyptische Jahre 88 Tage 22 Stunden 35 Minuten scheinbarer Zeit, welche mit der gleichmässigen übereinstimmt. In dieser Zeit sind 22577 Umläufe 179° 51′ vollendet, und dies stimmt mit dem, was wir schon entwickelt haben.
Um aber auch die Oerter dieser Bewegung für die früher angenommenen Anfänge festzustellen, haben wir noch zwei Mondfinsternisse hinzugenommen,
[225] nicht an demselben Knoten, auch nicht, wie im Vorhergehenden, in diametral entgegengesetzten, sondern in denselben, nördlichen oder südlichen Punkten; während nach der Vorschrift des Ptolomäus[80] alle übrigen Umstände, wie wir dieselben angegeben haben, gewahrt bleiben; und durch diese werden wir unsern Zweck fehlerfrei erreichen. Die erste Finsterniss, deren wir uns schon bei der Untersuchung der anderen Bewegungen des Mondes bedient haben[81], war diejenige von der wir gesagt haben, dass sie von Cl. Ptolomäus beobachtet ist, und zwar im 19ten Jahre Hadrian’s, nachdem zwei Tage des Monats Choiak verflossen waren, um eine Aequinoctialstunde Alexandriner Zeit vor Mitternacht, also nach Krakauer Zeit zwei Stunden vor Mitternacht, auf welche der dritte Tag folgte. Der Mond wurde um die Mitte der Finsterniss auf zehn Zwölftel des Durchmessers, d. h. zehn Zoll von Norden verfinstert, während die Sonne in 25° 10′ der Waage stand; der Ort der Anomalie des Mondes war 64° 38′ und ihre abzuziehende Prosthaphärese betrug 4° 20′ in der Gegend des absteigenden Knoten. Die zweite haben wir wieder mit grosser Sorgfalt zu Rom beobachtet, im Jahre Christi 1500 den 6ten November zwei Stunden nach der Mitternacht, welche den 6ten November anfing. Zu Krakau, das 5 Grade östlich liegt, war es zwei und zweifünftel Stunden nach Mitternacht, während die Sonne in 23° 16′[82] des Skorpions stand; es wurden wieder von Norden her 10 Zoll verfinstert. Dies sind also vom Tode Alexander’s 1824 ägyptische Jahre 84 Tage 14 Stunden 20 Minuten scheinbare, oder 14 Stunden 16 Minuten gleichmässige Zeit. Also war die mittlere Bewegung des Mondes 174° 14′, die Anomalie des Mondes 294° 40′, die ausgeglichene 291° 35′, die zu addirende Prosthaphärese 4° 28′. Es ist offenbar, dass der Mond bei diesen beiden Finsternissen auch einen gleichen Abstand von der grössten Abside hatte, auch war die Sonne bei beiden ungefähr in ihrer mittleren Abside, und die Grössen der Finsternisse waren gleich. Dies beweist, dass die südliche Breite des Mondes auch gleich war, und dass der Mond also gleiche Abstände von den Knoten hatte, aber hier aufsteigend, dort absteigend war. Es liegen nun zwischen beiden Finsternissen 1366 ägyptische Jahre 358 Tage 4 Stunden 20 Minuten scheinbare Zeit, gleichmässige aber 4 Stunden 24 Minuten, in welcher Zeit die mittlere Bewegung der Breite 159° 55′ beträgt.
[226] und = 4° 28′ hinzuaddirt wird: so wird der ganze Bogen = 168° 43′; der Rest des Halbkreises ist also 11° 17′ und dessen Hälfte 5° 39′ gleich gleich , nämlich gleich den wahren Abständen des Mondes von der Knotenlinie , und folglich ist = 9° 59′. Daraus ergiebt sich auch der mittlere Ort der Breite von der nördlichen Grenze, d. h. zu 99° 59′. Es sind aber bis zu diesem Orte und bis zu der Zeit der Ptolomäischen Beobachtung vom Tode Alexander’s 457 ägyptische Jahre 91 Tage 10 Stunden scheinbare, also 9 Stunden 54 Minuten gleichmässige Zeit verflossen, während welcher die Bewegung der Breite 50° 59′ betrug; wenn diese von 99° 59′ abgezogen werden, so bleiben 49° für den Mittag des ersten Tages des ersten ägyptischen Monats Thoth, zu Anfange der Jahre Alexanders. Dies ist aber auf den Meridian von Krakau bezogen. Hieraus sind auch für die übrigen Epochen, den Zeitdifferenzen gemäss, die Oerter der Breite des Mondes, von der nördlichen Grenze an gerechnet, gegeben und davon leiten wir die Bewegung selbst ab. Von der ersten Olympiade bis zum Tode Alexanders sind es 451 ägyptische Jahre 247 Tage, wovon zur Ausgleichung der Zeit 7 Minuten abgezogen werden. Zu dieser Zeit war der Ort der Breite 136° 57′. Von der ersten Olympiade bis auf Cäsar sind es 730 ägyptische Jahre 12 Stunden, denen zur Ausgleichung der Zeit 10 Minuten hinzugefügt werden. Zu dieser Zeit ist der gleichmässige Ort 206° 53′. Dann bis Christus 45 Jahre 12 Tage[83]. Wenn wieder von jenen 49° abgezogen werden 136° 57′, nachdem 360° hinzugefügt sind, so bleiben 272° 3′ für den Mittag des ersten Tages des Hekatombäon der ersten Olympiade. Wenn hierzu wieder 206° 53′ addirt werden, so kommen 118° 56′ für die Mitternacht des ersten Januar der julianischen Jahre; werden endlich 10° 49′ hinzuaddirt: so ergiebt sich der Ort Christi, ebenfalls um Mitternacht des ersten Januars, zu 129° 45′.
Dass die grösste Breite des Mondes, dem Neigungswinkel seiner Bahn gegen die Ekliptik entsprechend, fünf Grade beträgt, von denen 360 auf einen Kreis gehen, dies zu beobachten, hat uns das Schicksal nicht dieselbe Gelegenheit geboten, wie dem Cl. Ptolemäus, weil uns die Parallaxen des Mondes hinderlich waren. Dieser nämlich beobachtete zu Alexandrien, wo der Nordpol eine Höhe von 30° 58′ hat, bis zu welchem Grade der Mond sich dem Zenith am meisten näherte, also wenn er im Anfange des Krebses und in seiner nördlichen Grenze stand, was er schon durch die Rechnung vorauswissen konnte. Er fand nun damals mittelst eines Instrumentes, — welches er das parallactische nennt, und welches dazu eingerichtet war, die Parallaxen des Mondes zu messen, — den kleinsten Abstand des Mondes vom Zenith zu 2⅛°, bei welchem die Parallaxe, wenn überhaupt eine solche [227] stattfand, eben wegen dieses so kleinen Abstandes, eine nur sehr mässige[WS 10] sein musste. Zieht man 2⅛° von 30° 58′ ab, so bleiben 28° 51½′, was die grösste Schiefe der Ekliptik, die damals 23° 51′ 20″[85] betrug, um ungefähr 5 volle Grade übertrifft, und diese Breite des Mondes findet sich nach den übrigen Einzelnheiten bis heute übereinstimmend. Das parallactische Instrument besteht aus dreien Linealen, von denen zwei gleich und wenigstens vier Ellen lang sind, das dritte aber länger ist. Dieses und das eine der beiden anderen sind mit den beiden Enden des dritten durch kunstgerechte Durchbohrungen und dazu passende Axen oder Stifte so verbunden, dass sie sich in einer und derselben Ebene drehen, aber in jenen Gelenken durchaus nicht zittern können. Auf dem längeren Lineale ist, von dem Mittelpunkte seines Gelenkes, seiner ganzen Länge nach eine grade Linie eingeschnitten, auf welcher ein, dem so genau als möglich gemessenen Abstande der Gelenke gleiches Stück abgetragen ist. Dieses wird in tausend, oder wo möglich in mehr gleiche Theile getheilt, und diese Theilung auf der Verlängerung in gleicher Weise fortgesetzt, bis das Ganze 1414 Theile enthält. Dies ist die Länge der Seite eines Quadrates, welches in einen Kreis eingezeichnet werden kann, dessen Radius 1000 Theile enthält. Das Uebrige, um was dieses Lineal länger ist, kann als überflüssig abgeschnitten werden. Auch auf dem andern Lineale wird, von dem Mittelpunkte des Gelenkes aus, eine Linie gezeichnet, welche tausend jener Theile enthält, also dem Abschnitte zwischen den Mittelpunkten der Gelenke auf dem ersten Lineale gleich ist. Dasselbe trägt an der Seite Oeffnungen, wie es beim Diopter üblich ist, durch welche gesehen wird, und die so abgepasst sind, dass die Absehenslinie gegen die Linie, welche auf der Länge des Lineales gezeichnet ist, sich durchaus nicht neigt, sondern von derselben überall gleich weit absteht. Es ist auch dafür gesorgt, dass diese Linie, welche mit ihrem Ende an das längere Lineal reicht, die getheilte Linie treffen kann; so dass auf diese Weise aus den Linealen ein gleichschenkliges Dreieck gebildet wird, dessen Basis aus Theilen der eingetheilten Linie besteht. Hierauf wird ein sehr gut gekanteter und polirter Pfahl aufgerichtet und befestigt, an welchen das Instrument mit demjenigen Lineale, welches die beiden Gelenke trägt, mittelst einiger Hespen angefügt wird, in denen es sich wie eine Thür drehen kann; so zwar, dass die grade Linie, welche durch die Mittelpunkte der Gelenke des Lineales geht, immer senkrecht steht und auf das Zenith, wie die Axe des Horizontes, gerichtet ist. Will man nun die Zenithdistanz irgend eines Sternes finden, so sieht man, nachdem das Gestirn durch die Diopter des Lineals richtig visirt und das Lineal mit der getheilten Linie unterhalb beobachtet ist, wie viele Theile den Winkel spannen, welcher zwischen der Absehenslinie und der Axe des Horizontes liegt. Von diesen Theilen enthält der Durchmesser des Kreises 2000°, und man erhält aus dem Verzeichnisse den verlangten Bogen des grössten Kreises zwischen dem Gestirn und dem Zenith.
[228]Durch dieses Instrument erhielt, wie gesagt, Ptolemäus die grösste Breite des Mondes zu 5°. Hierauf wandte er sich zur Bestimmung der Parallaxe desselben, und sagt, dass er dieselbe in Alexandrien zu 1° 7′ gefunden habe, während die Sonne in 5° 28′ der Waage stand, die mittlere Distanz des Mondes und der Sonne 78° 13′, die gleichmässige Anomalie 262° 20′, die Bewegung der Breite 354° 40′, die zu addirende Prosthaphärese 7° 26′ und folglich der Ort des Mondes in 3° 9′ des Steinbocks war. Die gleichmässige Bewegung der Breite betrug 2° 6′, die nördliche Breite des Mondes 4° 59′, seine Declination vom Aequator 23° 49′, die Breite von Alexandrien 30° 58′. Es stand aber, wie er sagt, der Mond ungefähr im Meridiane und, nach der Beobachtung durch das Instrument, 50° 55′ vom Zenith, d. h. um 1° 7′ mehr als die Rechnung ergab. Hieraus beweist er, nach der Ansicht der Alten vom excentrischen Kreise und dem Epicykel, dass der Abstand des Mondes vom Mittelpunkte der Erde 3945/60 solcher Theile betrug, von denen der Erdhalbmesser einen darstellt, — und folgert weiter aus der Bewegung derselben Kreise, dass die grösste Entfernung des Mondes von der Erde, welche, wie man behauptet, im Apogeum des Epicykels beim Neu- und Vollmonde eintritt, 64⅙ derselben Theile, — die kleinste aber, welche bei den Quadraturen der Mondviertel und im Perigeum des Epicykels stattfinde, 3333/60 solcher Theile betrage. Hieraus ermittelte er auch die Parallaxen, welche bei 90° vom Zenith eintreten, und zwar die kleinste zu 53′ 34″, die grösste zu 1° 43′, wie man dies weiter aus dem ersehen kann, was er hierüber entwickelt hat. Es ist aber für den, der sehen will, schon von vornherein klar, dass sich dies weit anders verhält, wie wir uns vielfältig überzeugt haben. Zwei Beobachtungen wollen wir aber wieder besonders untersuchen, aus denen hervorgeht, dass unsere Annahmen über den Mond um so gewisser sind als jene, je mehr dieselben mit den Erscheinungen übereinstimmen, und keinerlei Zweifel übrig lassen. Im Jahre Christi 1522 den 27sten September nach Ablauf von 5⅔ gleichmässigen Stunden, Nachmittags bei Sonnenuntergänge fanden wir nämlich zu Frauenburg durch das parallactische Instrument den Abstand des Mittelpunktes des Mondes vom Zenith im Meridiane zu 82° 50′. Es waren mithin vom Anfange der Jahre Christi bis zu dieser Stunde 1522 ägyptische Jahre 284 Tage 17⅔ Stunden scheinbarer Zeit, also 17 Stunden 34 Minuten gleichmässiger Zeit verflossen. Nach der Rechnung war daher der scheinbare Ort der Sonne in 13° 29′ der Waage, die gleichmässige Bewegung des Mondes von der Sonne 87° 6′, die gleichmässige Anomalie 357° 39′, die wahre 358° 40′, die zu addirende Prosthaphärese 7′. Also war der wahre Ort des Mondes in 12° 33′ des Steinbocks. Die mittlere Bewegung der Breite von der nördlichen Grenze betrug 197° 1′, die wahre 197° 8′, die südliche Breite des Mondes 4° 47′, die Declination vom Aequator 27° 41′, die Breite unsres [229] Beobachtungsortes 54° 19′, welche mit der Declination des Mondes zusammen den wahren Abstand vom Zenith zu 82° ergiebt. Folglich kamen die übrigen 50′ auf die Parallaxe, welche nach der Ueberlieferung des Ptolemäus 1° 17′ hätte sein müssen. Die zweite Beobachtung haben wir wieder an demselben Orte angestellt im Jahre Christi 1524 den 7ten August nach Ablauf von 6 Stunden Nachmittags, und durch dasselbe Instrument den Mond um 81° 55′ vom Zenith entfernt gefunden. Es waren also vom Anfange der Jahre Christi bis zu dieser Stunde 1524 ägyptische Jahre 234 Tage 18 scheinbare Stunden, welche auch 18 gleichmässige Stunden waren, verflossen. Nun war der Ort der Sonne nach der Berechnung in 24° 14′ des Löwen, die mittlere Bewegung des Mondes von der Sonne 97° 6′, die gleichmässige Anomalie 242° 10′, die ausgeglichene 239° 40′, die zu der mittleren Bewegung hinzuzuaddirende Prosthaphärese nahe 7°. Also war der wahre Ort des Mondes in 9° 39′ des Schützen. Die mittlere Bewegung der Breite betrug 193° 19′, die wahre 200° 17′, die südliche Breite des Mondes 4° 41′, die südliche Declination 26° 36′, welche mit der Breite des Beobachtungsortes, nämlich 54° 19′, als Zenithdistanz des Mondes 80° 55′ ergiebt; die scheinbare Zenithdistanz war aber 82°, also kam der Ueberschuss von 1° 5′ auf die Parallaxe des Mondes, welche nach Ptolemäus und der Meinung der Früheren 1° 38′ hätte sein müssen, weil das harmonische Verhältniss, welches aus ihrer Annahme folgt, dies verlangt.


[231] in Bezug auf den Horizont, an welchem die Parallaxen bekanntlich ihre volle Grösse erhalten, dieselben vollständiger zu messen, und doch fanden wir, dass die Parallaxen um nicht mehr, als um eine Minute verschieden sind.
Neben der Entfernung des Mondes von der Erde sind auch die scheinbaren Durchmesser des Mondes und des Schattens veränderlich, weshalb wir auch von diesen reden müssen. Obgleich die Durchmesser der Sonne und des Mondes mittelst des Diopters des Hipparch richtig gemessen werden, so glaubt man doch, dies beim Monde viel genauer erreichen zu können mit Hülfe einiger auserwählter Mondfinsternisse, bei denen der Mond um gleich viel von seiner grössten und kleinsten Abside absteht; zumal wenn alsdann die Sonne in gleicher Weise sich dem so anschliesst, dass der Schattenkreis, welchen der Mond bei jeder derselben zu durchlaufen hat, gleich befunden wird; nur dass die Finsternisse sich auf ungleiche Theile erstrecken. Es ist nämlich offenbar, dass der Unterschied zwischen den verfinsterten Theilen und den entsprechenden Breiten des Mondes auf die Grösse des Bogens eines um den Mittelpunkt der Erde beschriebenen Kreises schliessen lässt, welchen der Durchmesser des Mondes einnimmt; — kennt man aber diesen, so findet man auch bald den Halbmesser des Schattens. Dies mag an einem Beispiele deutlicher gemacht werden. Wenn also zur Zeit der Mitte einer früheren Finsterniss drei Zoll vom Halbmesser des Mondes verfinstert sind, während seine Breite 47′ 54″ beträgt, und bei einer späteren, bei welcher die Breite 29′ 37″ war, zehn Zoll verfinstert wurden, so ist der Unterschied zwischen den Grössen der Finsternisse sieben Zoll, und derjenige zwischen den Breiten 18′ 17″, während 31′ 20″, als der scheinbare Durchmesser des Mondes, zwölf Zollen entsprechen. Es ergiebt sich also, dass der Mittelpunkt des Mondes zur Zeit der Mitte der ersten Finsterniss um den vierten Theil des Durchmessers desselben aus dem Schatten hervorragte, diesem entsprechen 7′ 50″ der Breite; und zieht man diese von den 47′ 54″ der ganzen Breite ab, so bleiben 40′ 4″ für den Halbmesser des Schattens. Ebenso reichte bei der zweiten Finsterniss der Schatten um den dritten Theil des Monddurchmessers, also um eine Breite von 10′ 27″, über den Mittelpunkt des Mondes hinaus; addirt man diese zu den 29′ 37″, so erhält man ebenfalls 40′ 4″ für den Halbmesser des Schattens[88]. Freilich ist des Ptolemäus’ Meinung, dass, während Sonne und Mond bei ihrer Conjunction und Opposition in ihren grössten Entfernungen von der Erde stehen, der Durchmesser des Mondes 31′ 20″ beträgt, und ebenso gross, behauptet er, den Durchmesser der Sonne durch das Diopter des Hipparch gefunden zu haben. Der Durchmesser des Schattens soll aber 1° 21′ 20″ sein, [232] und er glaubte, dass diese Grössen sich zu einander wie 13 zu 5 verhielten, so dass der Durchmesser des Schattens 2⅗ mal so gross sei, als derjenige des Mondes und der Sonne.

[233] betragen, von denen die Einheit ist; sei der Durchmesser des Schattens an der Stelle des Durchganges des Mondes, sei der Durchmesser des Mondes, rechtwinklig gegen und werde bis verlängert. Zuerst soll nun das Verhältniss von zu gefunden werden. Da der Winkel 31′ 20″ beträgt, so ist die Hälfte gleich 15′ 40″ und der Winkel bei ist ein Rechter. In dem Dreiecke sind also die Winkel gegeben, und folglich auch das Verhältniss der Seiten zu , und seiner Länge nach 1733/60 Sechzigstel solcher Theile, von denen 64⅙ oder einen Theil enthält; und weil sich zu verhalten soll wie 5 zu 13: so enthält 4538/60 Sechzigstel derselben Theile. Da aber und in gleichen Abständen mit parallel sind: so ist und zusammen doppelt so gross als ; zieht man davon und ab: so bleibt gleich 5649/60 Sechzigstel. Nach dem zweiten Lehrsatze des sechsten Buches Euklid’s verhalten sich zu , zu und zu wie zu , d. h. wie 60 zu 5649/60[90]. Ebenso ergiebt sich zu 5649/60, wenn 60 ist, und der Rest zu 311/60. Insofern aber 64⅙ solcher Theile enthält, deren einer ist: so kommen auf 1210. Nun hat sich schon gezeigt, dass 4538/60 Sechzigstel solcher Theile enthält, und es besteht das Verhältniss zu wie zu , folglich enthält auch 1422/60 Sechzigstel von ; und umgekehrt, wenn 64⅙ enthält: so kommen auf , als auf die Axe des Schattens, 268.[91]. So Ptolomäus. Andere aber, nach Ptolomäus, stellten, als sie fanden, dass dies den Erscheinungen nicht genügend entspreche, gewisse andere Annahmen auf. Nichts desto weniger behaupten sie, dass die grösste Entfernung des vollen und neuen Mondes von der Erde 64⅙ Erdradien sei, der scheinbare Durchmesser der Sonne im Apogeum 31′ 20″ betrage und sich zu dem Durchmesser des Schattens an der Stelle des Durchgangs des Mondes verhalte, wie 13 zu 5, ganz wie Ptolomäus selbst. Sie sagen jedoch, dass der scheinbare Durchmesser des Mondes alsdann nicht grösser sei als 29½′, setzen deshalb den Durchmesser des Schattens gleich 1° 16′ 45″, glauben, dass hieraus die Entfernung der Sonne von der Erde gleich 1146 und die Axe des Schattens gleich 254 Erdradien folge, und schreiben diese Entdeckung, welche jedoch nicht begründet werden kann, jenem aratäischen Philosophen[92] zu. Wir haben aber dies so in Ordnung bringen und verbessern müssen, dass wir den scheinbaren Durchmesser der Sonne im Apogeum zu 31′ 40″ ansetzten, (er muss nämlich gegenwärtig etwas grösser sein, als vor Ptolomäus); denjenigen des vollen und neuen Mondes aber, und zwar in seiner grössten Abside, zu 30′ und denjenigen des Schattens an der Stelle des Durchganges des Mondes zu 80′ 36″: denn es passt besser, dass dies Verhältniss wie 150 zu 403, also etwas grösser ist, als 5 zu 13. Die ganze Sonnenscheibe kann aber vom Monde nur dann bedeckt werden, wenn dieser von der Erde um 62 Erdhalbmesser absteht. Wenn man dies so annimmt, so scheint es sowohl unter sich als auch mit dem Uebrigen in zuverlässiger Weise zusammenzuhängen und mit den Erscheinungen der Sonnen- und Mondfinsternisse übereinzustimmen. Wenn wir [234] nach den vorangegangenen Entwickelungen Alles in ganzen und sechzigsteln Erdradien ausdrücken: so erhalten wir gleich 178/60 Sechzigstel, daher gleich 461/60 Sechzigstel, folglich gleich 5651/60 Sechzigstel und die ganze Linie gleich 1179 ganze Theile, als Entfernung der Sonne von der Erde im Apogeum, und die Axe des Schattens gleich 265 ganze Theile.

Da aber dieselben Grössen in grösserer Entfernung kleiner erscheinen, als in der Nähe: so verändern sich Sonne, Mond und Erdschatten nach ihren verschiedenen Entfernungen von der Erde nicht weniger, als die Parallaxen; und Alles dies wird nach dem Vorhergehenden leicht für jede beliebige Entfernung berechnet. Zuerst ist dies bei der Sonne offenbar. Da wir nämlich gezeigt haben, dass die Erde bei ihrer grössten Entfernung von der Sonne um 10323 solcher Theile absteht, [235] von denen der Halbmesser des jährlichen Umlaufkreises 10000 enthält, und bei ihrer grössten Nähe 9678: so beträgt die grösste Abside 1179 Erdradien, also die kleinste 1105 und folglich die mittlere 1142. Wenn wir nun mit 1179 in eine Million dividiren: so erhalten wir 848 als die Kathete, welche in dem rechtwinkeligen Dreiecke dem kleinsten Winkel gegenüberliegt, und dieser ist daher 2′ 55″ als die grösste Parallaxe, welche am Horizonte eintritt. Dividirt man ebenso mit der kleinsten Entfernung, also mit 1105 in eine Million: so kommen 905 heraus, und dies ergiebt für den Winkel der grössten Parallaxe bei der kleinsten Abside 3′ 7″. Es ist aber gezeigt, dass der Durchmesser der Sonne 527/60 Erddurchmesser beträgt, welche Grösse in der grössten Abside unter einem Winkel von 31′ 48″ erscheint. Denn 1179 verhält sich zu 527/60 wie 200000 zu 9245, welches die Sehne für einen Winkel von 31′ 48″ ist. Es folgt daraus, dass der Sonnendurchmesser in der kleinsten Entfernung von 1105 Erdradien unter einem Winkel von 33′ 54″ erscheint. Die Differenz hiervon beträgt 2′ 6″, diejenige der Parallaxen aber nur 12″. Ptolemäus ist der Meinung, dass beide wegen ihrer Kleinheit zu vernachlässigen wären, in Anbetracht, dass eine oder zwei Minuten nicht leicht mit dem Auge aufgefasst wird, und dies bei Secunden noch viel weniger möglich ist. Wenn wir daher die grösste Parallaxe von 3′ überall beibehalten: so werden wir keinen Fehler zu begehen scheinen. Die mittleren scheinbaren Durchmesser der Sonne erhalten wir aber aus den mittleren Abständen, oder, wie Einige, aus der scheinbaren stündlichen Bewegung der Sonne, deren Verhältniss zu ihrem Durchmesser sie auf 5 : 66 oder 1 zu 14⅕ schätzen. Die stündliche Bewegung der Sonne ist aber ihrer Entfernung nahezu proportional.
Beide Unterschiede erscheinen beim Monde, als dem näheren Gestirne, grösser. Denn während die grösste Entfernung von der Erde bei Neu- und Vollmond 65½ beträgt, ist nach den obigen[93] Entwickelungen, die kleinste 558/60; bei den Mondvierteln beträgt aber die grösste Entfernung 6821/60 und die kleinste 5217/60. Aus diesen vier Zahlenbestimmungen erhalten wir die Parallaxen des auf- oder untergehenden Mondes, wenn wir den Erdradius durch die Entfernung des Mondes von der Erde dividiren; und zwar ergiebt sich für die grösste Entfernung des Mondviertels 50′ 18″, für diejenige des Voll- und Neumondes 52′ 24″; für die kleinste Entfernung des Voll- und Neumondes 62′ 21″ und für die kleinste des Mondviertels 65′ 45″. Hieraus ergeben sich denn auch die scheinbaren Durchmesser des Mondes. Es ist nämlich nachgewiesen, dass der Durchmesser der Erde sich zu dem des Mondes verhält wie 7 zu 2, also verhält sich der Erdradius zu dem Durchmesser [236] des Mondes wie 7 zu 4, und in diesem Verhältnisse stehen auch die Parallaxen zu den Winkeln der scheinbaren Durchmesser des Mondes. Da nun das Verhältniss der graden Linien, welche die Winkel der Parallaxen einschliessen, zu den scheinbaren Durchmessern, bei demselben Durchgange des Mondes, sich gar nicht ändert, und die Winkel ihren gradlinigen Sehnen nahe proportional sind, so bleibt ihre Veränderung für die Beobachtung unmerklich. Berücksichtigt man dieselben daher nicht, so ist klar, dass bei der ersten Grenze[94] der eben dargelegten Parallaxen, der scheinbare Durchmesser des Mondes 28′ 45″, bei der zweiten nahe 30′, bei der dritten 35′ 38″ und bei der letzten 37′ 34″ beträgt. Diese Letztere würde nach der Annahme des Ptolomäus und Anderer nahe einen Grad betragen, und es müsste sich dann ereignen, dass der zu jener Zeit mit halbem Lichte leuchtende Mond ebensoviel Licht zur Erde sendete, als der volle Mond.

Wir haben schon[95] nachgewiesen, dass sich der Durchmesser des Schattens zum Durchmesser des Mondes verhalte, wie 403 zu 150, und deshalb wird derselbe beim Voll- und Neumonde, während die Sonne im Apogeum steht, am kleinsten, nämlich gleich 80⅗′, und am grössten gleich 95′ 44″ gefunden, und die grösste Differenz beträgt 15′ 8″[96]. Es verändert sich aber der Erdschatten, bei sich gleichbleibendem Durchgange des Mondes, wegen der ungleichen Entfernung der Erde von der Sonne in folgender Weise: Man nehme wieder, wie in der vorigen Figur, als die durch die Mittelpunkte der Sonne und der Erde gelegte grade Linie , ziehe die Tangente , und die beiden graden und . Nun ist bewiesen, dass, während die Entfernung 1179 Erdradien beträgt, und deren 62 enthält, der Halbmesser des Schattens 461/60 Sechzigstel Erdradien, und, nachdem gezogen ist, der Winkel des scheinbaren Halbmessers 42′ 32″ und die Axe des Schattens gleich 265 Erdradien ist. Wenn aber die Erde der Sonne am nächsten steht, wo gleich 1105 Erdradien ist, werden wir den Schatten der Erde bei sich gleichbleibendem Durchgange des Mondes, auf folgende Weise berechnen. Es werde parallel zu gezogen; dann verhält sich zu wie zu ; nun ist aber gleich 427/60, und gleich 1105 Erdradien, denn in dem Parallelogramm ist gleich und gleich : folglich ist gleich 24819/60 Erdradien. Aber betrug 62 derselben Theile, und folglich [237] der Rest 18619/60. Da sich aber verhalten zu , wie zu : so ist auch gleich 451/60 Sechzigstel Erdradius, und dann ist der Winkel des scheinbaren Halbmessers gleich 41′ 35″. Durch die grössere oder geringere Entfernung der Sonne von der Erde tritt also bei gleichem Durchgange des Mondes in dem Durchmesser des Schattens eine grösste Differenz von einem Sechzigstel Erdradius ein, oder im Winkel des scheinbaren Durchmessers eine solche von 1′ 54″, d. h. von 57″ wenn 360° gleich vier Rechten sind. Ferner ist das Verhältniss des Schattendurchmessers zum Durchmesser des Mondes nur wenig dort grösser, hier kleiner, als das mittlere vom 13 zu 5, deswegen werden wir einen nur geringen Fehler begehen, wenn wir, um Arbeit zu ersparen, dasselbe überall anwenden, indem wir der Ansicht der Alten folgen.



[240]
TAFEL DER SONNEN- UND MOND-PARALLAXEN.
| |||||||||||||
| Gemeinschaftliche Zahlen | Sonnen-Parallaxen | Abzuziehende Differenz der Mondparallaxe 1. u. 2. Grenze | Mondparallaxe der 2. Grenze | Mondparallaxe der 3. Grenze | Zu addirende Differenz der Mondparallaxe 3. u. 4. Grenze | Proportional-Minuten | |||||||
| Grad | Grad | Min. | Sec. | Min. | Sec. | Min. | Sec. | Min. | Sec. | Min. | Sec. | des kleinen Epicykels | des grossen Epicykels |
| 6 | 354 | 0 | 10 | 0 | 7 | 2 | 46 | 3 | 18 | 0 | 12 | 0 | 0 |
| 12 | 348 | 0 | 19 | 0 | 14 | 5 | 33 | 6 | 36 | 0 | 23 | 1 | 0 |
| 18 | 342 | 0 | 29 | 0 | 21 | 8 | 19 | 9 | 53 | 0 | 34 | 3 | 1 |
| 24 | 336 | 0 | 38 | 0 | 28 | 11 | 4 | 13 | 10 | 0 | 45 | 4 | 2 |
| 30 | 330 | 0 | 47 | 0 | 35 | 13 | 49 | 16 | 26 | 0 | 56 | 5 | 3 |
| 36 | 324 | 0 | 56 | 0 | 42 | 16 | 32 | 19 | 40 | 1 | 6 | 7 | 5 |
| 42 | 318 | 1 | 5 | 0 | 48 | 19 | 5 | 22 | 47 | 1 | 16 | 10 | 7 |
| 48 | 312 | 1 | 13 | 0 | 55 | 21 | 39 | 25 | 47 | 1 | 26 | 12 | 9 |
| 54 | 306 | 1 | 22 | 1 | 1 | 24 | 9 | 28 | 49 | 1 | 35 | 15 | 12 |
| 60 | 300 | 1 | 31 | 1 | 8 | 26 | 36 | 31 | 42 | 1 | 45 | 18 | 14 |
| 66 | 294 | 1 | 39 | 1 | 14 | 28 | 57 | 34 | 31 | 1 | 54 | 21 | 17 |
| 72 | 288 | 1 | 40 | 1 | 19 | 31 | 14 | 37 | 14 | 2 | 3 | 24 | 20 |
| 78 | 282 | 1 | 53 | 1 | 24 | 33 | 25 | 39 | 50 | 2 | 11 | 27 | 23 |
| 84 | 276 | 2 | 0 | 1 | 29 | 35 | 31 | 42 | 19 | 2 | 19 | 30 | 26 |
| 90 | 270 | 2 | 7 | 1 | 34 | 37 | 31 | 44 | 40 | 2 | 26 | 34 | 29 |
| 96 | 264 | 2 | 13 | 1 | 39 | 39 | 24 | 46 | 54 | 2 | 33 | 37 | 32 |
| 102 | 258 | 2 | 20 | 1 | 44 | 41 | 10 | 49 | 0 | 2 | 40 | 39 | 35 |
| 108 | 252 | 2 | 26 | 1 | 48 | 42 | 50 | 50 | 59 | 2 | 46 | 42 | 38 |
| 114 | 246 | 2 | 31 | 1 | 52 | 44 | 24 | 52 | 49 | 2 | 53 | 45 | 41 |
| 120 | 240 | 2 | 36 | 1 | 56 | 45 | 51 | 54 | 30 | 3 | 0 | 47 | 44 |
| 126 | 234 | 2 | 40 | 2 | 0 | 47 | 8 | 56 | 2 | 3 | 6 | 49 | 47 |
| 132 | 228 | 2 | 44 | 2 | 2 | 48 | 15 | 57 | 23 | 3 | 11 | 51 | 49 |
| 138 | 222 | 2 | 49 | 2 | 3 | 49 | 15 | 58 | 36 | 3 | 14 | 53 | 52 |
| 144 | 216 | 2 | 52 | 2 | 4 | 50 | 10 | 59 | 39 | 3 | 17 | 55 | 54 |
| 150 | 210 | 2 | 54 | 2 | 4 | 50 | 55 | 60 | 31 | 3 | 20 | 57 | 56 |
| 156 | 204 | 2 | 56 | 2 | 5 | 51 | 29 | 61 | 12 | 3 | 22 | 58 | 57 |
| 162 | 198 | 2 | 58 | 2 | 5 | 51 | 56 | 61 | 47 | 3 | 23 | 59 | 58 |
| 168 | 192 | 2 | 59 | 2 | 6 | 52 | 13 | 62 | 9 | 3 | 23 | 59 | 59 |
| 174 | 186 | 3 | 0 | 2 | 6 | 52 | 22 | 62 | 19 | 3 | 24 | 60 | 60 |
| 180 | 180 | 3 | 0 | 2 | 6 | 52 | 24 | 62 | 21 | 3 | 24 | 60 | 60 |
[241]
TAFEL DER HALBMESSER DER SONNE, DES MONDES UND DES SCHATTENS.
| |||||||||||
| Gemeinschaftliche Zahlen | Halbmesser der Sonne | Halbmesser des Mondes | Halbmesser des Schattens nach dem Manuscript | Halbmesser des Schattens nach den Ausgaben | Veränderung des Schattens nach dem Manuscript. | Veränderung des Schattens nach den Ausgaben. | |||||
| Grad | Grad | Min. | Sec. | Min. | Sec. | Min. | Sec. | Min. | Sec. | Minuten | Minuten |
| 6 | 354 | 15 | 50 | 15 | 0 | 39 | 30 | 40 | 18 | 0 | 0 |
| 12 | 348 | 15 | 50 | 15 | 1 | 39 | 32 | 40 | 21 | 0 | 0 |
| 18 | 342 | 15 | 51 | 15 | 3 | 39 | 37 | 40 | 26 | 1 | 1 |
| 24 | 336 | 15 | 52 | 15 | 6 | 39 | 48 | 40 | 34 | 2 | 2 |
| 30 | 330 | 15 | 53 | 15 | 9 | 39 | 52 | 40 | 42 | 3 | 3 |
| 36 | 324 | 15 | 55 | 15 | 14 | 40 | 7 | 40 | 56 | 4 | 4 |
| 42 | 318 | 15 | 57 | 15 | 19 | 40 | 23 | 41 | 10 | 6 | 6 |
| 48 | 312 | 16 | 0 | 15 | 25 | 40 | 40 | 41 | 26 | 8 | 9 |
| 54 | 306 | 16 | 3 | 15 | 32 | 40 | 58 | 41 | 44 | 10 | 11 |
| 60 | 300 | 16 | 6 | 15 | 39 | 41 | 16 | 42 | 2 | 12 | 14 |
| 66 | 294 | 16 | 9 | 15 | 47 | 41 | 36 | 42 | 24 | 14 | 16 |
| 72 | 288 | 16 | 12 | 15 | 56 | 41 | 58 | 42 | 40 | 17 | 19 |
| 78 | 282 | 16 | 15 | 16 | 5 | 42 | 21 | 43 | 13 | 19 | 22 |
| 84 | 276 | 16 | 19 | 16 | 13 | 42 | 43 | 43 | 34 | 22 | 25 |
| 90 | 270 | 16 | 22 | 16 | 22 | 43 | 5 | 43 | 58 | 24 | 27 |
| 96 | 264 | 16 | 26 | 16 | 30 | 43 | 27 | 44 | 20 | 27 | 31 |
| 102 | 258 | 16 | 29 | 16 | 39 | 43 | 50 | 44 | 44 | 29 | 33 |
| 108 | 252 | 16 | 32 | 16 | 47 | 44 | 12 | 45 | 6 | 32 | 36 |
| 114 | 246 | 16 | 36 | 16 | 55 | 44 | 34 | 45 | 20 | 34 | 39 |
| 120 | 240 | 16 | 39 | 17 | 4 | 44 | 56 | 45 | 52 | 37 | 42 |
| 126 | 234 | 16 | 42 | 17 | 12 | 45 | 16 | 46 | 13 | 39 | 45 |
| 132 | 228 | 16 | 45 | 17 | 19 | 45 | 36 | 46 | 32 | 41 | 47 |
| 138 | 222 | 16 | 48 | 17 | 26 | 45 | 54 | 46 | 51 | 43 | 49 |
| 144 | 216 | 16 | 50 | 17 | 32 | 46 | 10 | 47 | 7 | 45 | 51 |
| 150 | 210 | 16 | 53 | 17 | 38 | 46 | 24 | 47 | 23 | 47 | 53 |
| 156 | 204 | 16 | 54 | 17 | 41 | 46 | 33 | 47 | 31 | 48 | 54 |
| 162 | 198 | 16 | 55 | 17 | 44 | 46 | 41 | 47 | 39 | 48 | 55 |
| 168 | 192 | 16 | 56 | 17 | 46 | 46 | 48 | 47 | 44 | 49 | 56 |
| 174 | 186 | 16 | 57 | 17 | 48 | 46 | 53 | 47 | 49 | 49 | 56 |
| 180 | 180 | 16 | 57 | 17 | 49 | 46 | 55 | 47 | 52 | 50 | 57 |
Wir wollen noch das Verfahren, wie die Sonnen- und Mond-Parallaxen aus der Tafel zu berechnen sind, kurz auseinandersetzen. Mittelst der doppelten Zenithdistanz der Sonne und des Mondes entnehmen wir die daneben stehenden Parallaxen, und zwar bei der Sonne einfach, beim Monde aber für seine vier Grenzen; und mittelst der doppelten Bewegung des Mondes, oder seines doppelten Abstandes von der Sonne, die ersten Proportionaltheile. Diese Letzteren verhalten sich zu 60 wie die zu findende Correction zu der Differenz der ersten und zweiten oder der dritten und vierten Grenze; dadurch ergeben sich die Correctionen, deren erste wir von der nächst folgenden Parallaxe der zweiten Grenze immer abziehen; deren zweite wir aber zu der nächst vorangehenden Parallaxe der dritten Grenze immer addiren. So erhalten wir die rectificirten beiden Mondparallaxen für das Apogeum und Perigeum, welche der kleine Epicykel vermehrt oder vermindert. Hierauf nehmen wir mit der ausgeglichenen einfachen Anomalie des Mondes die letzten Proportionaltheile und diese verhalten sich zu 60 wie die zu findende Correction zu der Differenz der eben gefundenen rectificirten beiden Mondparallaxen; hieraus ergiebt sich die Correction, welche wir zu der ersten rectificirten Parallaxe, die im Apogeum eintritt, immer addiren; von der zweiten rectificirten Parallaxe dagegen, die im Perigeum stattfindet, immer abziehen: und so erhält man die verlangte Parallaxe für Ort und Zeit, wie in dem folgenden Beispiele. Es sei die Zenithdistanz des Mondes 54°, die mittlere Bewegung des Mondes 15°, seine ausgeglichene Anomalie 100°; hieraus will ich durch die Tafel die Mondparallaxe finden. Die doppelte Zenithdistanz ist 108°, dieser entspricht die Differenz zwischen den Parallaxen der ersten und zweiten Grenze gleich 1′ 48″, die Parallaxe der zweiten Grenze ist gleich 42′ 50″, die Parallaxe der dritten Grenze 50′ 59″, die Differenz der Parallaxen der dritten und vierten Grenze 2′ 46″, was ich jedes besonders notire. Die doppelte Bewegung des Mondes ergiebt 30°, hiermit finde ich die ersten Proportionaltlieile gleich 5; nun verhält sich 5 zu 60 wie die zu findende Correction zu der Differenz der Parallaxen der ersten und zweiten Grenze, d. h. zu 108″; dies ergiebt die zu findende Correction gleich 9″, welche ich von den 42′ 50″ der Parallaxe zweiter Grenze abziehe, es bleiben, als rectificirte Parallaxe, 42′ 41″. Ebenso verhält sich 5 zu 60, wie die zu findende Correction zu der Differenz der Parallaxen der dritten und vierten Grenze, d. h. zu 166″; dies ergiebt die zu findende Correction gleich 14″, welche ich zu den 50′ 59″ der Parallaxe dritter Grenze addire, es werden als rectificirte Parallaxe 51′ 13″. Die Differenz dieser beiden rectificirten Parallaxen beträgt 8′ 32″. Hierauf nehme ich mit der einfachen ausgeglichenen Anomalie die letzten Proportionaltheile gleich 34; nun verhält sich 34 zu 60 wie die zu findende Correction zu der Differenz [243] der beiden rectificirten Parallaxen, d. h. zu 512″; dies ergiebt die zu findende Correction gleich 4′ 50″; dies addire ich zu der ersten ausgeglichenen Parallaxe und erhalte 47′ 31″, und dies ist die verlangte Parallaxe des Mondes im Verticalkreise.[98] Da aber die übrigen Mondparallaxen von denjenigen, welche beim vollen und neuen Monde stattfinden, so wenig verschieden sind, so scheint es auszureichen, wenn wir uns immer zwischen den mittleren Grenzen halten, welche wir zur Vorausbestimmung der Finsternisse am meisten gebrauchen. Im Uebrigen bedarf es nicht einer so grossen Genauigkeit, da sie vielleicht weniger der Anwendung als der Neugier dienen möchte.



[245] noch der Winkel und der Rechte gegeben sind. Daraus erhalten wir die übrigen Seiten und , und daraus wieder, wenn man von abzieht, als Parallaxe der Länge, und, wenn man die scheinbare Breite von der wahren Breite abzieht, als Rest die Parallaxe der Breite. Indessen bietet, wie man sieht, die Rechnung mehr Arbeit als Früchte dar, da es sich um sehr kleine Grössen handelt. Es wird daher genügen, wenn wir statt des Winkels den Winkel , und statt des Winkels den Winkel anwenden, und einfach, wie früher, für die Bogen und , mit Vernachlässigung der Breite des Mondes, immer den mittleren Bogen setzen. Daraus wird kein Fehler entstehen, zumal in den Gegenden der nördlichen Seite; in sehr südlichen Gegenden, wo dem Zenith nahe kommt, beträgt die Differenz bei der grössten Breite von fünf Graden, und wenn der Mond in seiner grössten Erdnähe steht, nahe sechs Minuten. Bei Sonnenfinsternissen jedoch, bei welchen der Mond nicht über anderthalb Grad abweichen darf, kann die Differenz nur zu 1¾ Minuten anwachsen. Hieraus ist also klar, dass die Parallaxe der Länge, wenn der Mund im östlichen Quadranten der Ekliptik steht, zu dem wahren Orte des Mondes immer addirt wird; liegt aber der wahre Ort des Mondes in dem andern Quadranten der Ekliptik: so wird die Parallaxe der Länge von demselben abgezogen, um die scheinbare Länge des Mondes zu erhalten. Auch die scheinbare Breite erhalten wir aus der Parallaxe der Breite, indem wir letztere addiren, wenn sie auf derselben Seite liegt; liegen beide aber auf verschiedenen Seiten: so zieht man die kleinere von der grösseren ab, und was übrig bleibt ist die scheinbare Breite, nach derjenigen Seite hin, auf welcher die grössere von beiden liegt.
Dass nun die so entwickelten Parallaxen des Mondes mit den Erscheinungen übereinstimmen, können wir durch mehrere andere Beobachtungen bestätigen. Eine solche haben wir zu Bologna am 9ten März nach Sonnenuntergang im Jahre Christi 1497 angestellt. Wir beobachteten nämlich den Mond, bei seiner bevorstehenden Bedeckung des glänzenden Sternes der Hyaden, welchen die Römer Palilicium[99] nennen, und sahen bei diesem Abwarten am Ende der 5ten Stunde der Nacht den Stern dicht an dem dunkeln Theile des Mondkörpers zwischen den Hörnern des Mondes eben verschwinden, um den dritten Theil des Monddurchmessers dem südlichen Horne näher. Und da der Stern nach der Berechnung in 2° 52′ der Zwillinge stand, bei einer südlichen Breite von 5⅙°, so war klar, dass der Mittelpunkt des Mondes dem Sterne scheinbar um den halben Durchmesser voraus, und deshalb sein scheinbarer Ort in Länge 2° 36′ und in Breite nahezu 5° 6′ war. Vom Anfange der Jahre Christi waren nun 1497 ägyptische [246] Jahre 76 Tage 23 Stunden Bologner Zeit verflossen, und da Krakau fast 9° östlicher liegt: so war die Krakauer Zeit 23 Stunden 36 Minuten, denen die Ausgleichung noch 4 Minuten hinzufügt. Die Sonne stand in 28½° der Fische, die gleichmässige Bewegung des Mondes von der Sonne war 74°, die ausgeglichene Anomalie 111° 10′, der wahre Ort des Mondes in 3° 24′ der Zwillinge, die südliche Breite 4° 35′, die wahre Bewegung der Breite 203° 41′. Damals ging zu Bologna der 26ste Grad des Skorpions unter einem Winkel von 59½° auf, und die Zenithdistanz des Mondes betrug 83°, der Neigungswinkel des Verticalkreises und der Ekliptik war ungefähr 29°, die Parallaxe des Mondes in der Länge war 1° 51′, in der Breite 30′, was so sehr der Beobachtung entspricht, dass man um so weniger an der Richtigkeit unserer Annahmen und dessen, was daraus folgt, zweifeln darf.
Aus dem, was bisher über die Bewegung des Mondes und der Sonne gesagt ist, ergiebt sich auch der Weg, ihre Conjunctionen und Oppositionen zu untersuchen. Für die Zeit nämlich, welche derjenigen einer Conjunction oder Opposition nach der Schätzung nahe liegt, suchen wir die gleichmässige Bewegung des Mondes; ergiebt sich dieselbe grade so gross als der ganze Kreis, so erkennen wir die Conjunction; der Halbkreis ergiebt uns den Vollmond. Da aber dies nur selten zutreffen wird: so muss der Abstand zwischen beiden beobachtet und dieser durch die tägliche Bewegung des Mondes dividirt werden, um zu erfahren, um wie viel Zeit eine von beiden Erscheinungen vergangen oder bevorstehend ist, je nachdem die Bewegung sich grösser oder kleiner ergiebt. Für diese Zeit suchen wir nun die Bewegungen und die Oerter, berechnen durch dieselben die wahren Neu- und Vollmonde, und unterscheiden die Finsternisse von den übrigen, wie wir weiter unten angeben wollen. Wenn wir dies einmal festgestellt haben: so lässt sich dasselbe auf beliebige andere Zeitpunkte und also auch auf eine Anzahl Jahre hinaus anwenden; und zwar mit Hülfe der Tafel, welche die Zeiten der zwölf Monate und der gleichmässigen Bewegungen der Anomalie der Sonne und des Mondes und der Breite des Mondes enthält, deren jede Einzelne mit den einzelnen schon früher gefundenen gleichmässigen Bewegungen zu verbinden ist. Wir fügen aber die ausgeglichene Anomalie der Sonne hinzu, damit wir dieselbe gleich zur Hand haben; ihre Aenderung wird nämlich wegen der Langsamkeit ihres Anfanges, d. h. der grössten Abside, in einem oder einigen Jahren nicht bemerkt.
[247]
TAFEL DER CONJUNCTION UND OPPOSITION DER SONNE UND DES MONDES.
| |||||||||||||||
| Monate | Zeiten | Bewegung der Anomalie des Mondes | Bewegung der Breite des Mondes | ||||||||||||
| Tage | nach Mnscrpt. | nach Ausgab. | Sechzig | Grad | Minuten | Sec. nach Manuscript | Sec. nach Ausgaben | Sechzig | Grad | Minuten | Sec. nach Manuscript | Sec. nach Ausgaben | |||
| 1 | 29 | 31 | 50 | 8 | 9 | 0 | 25 | 49 | 0 | 0 | 0 | 30 | 40 | 13 | 14 |
| 2 | 59 | 3 | 40 | 16 | 18 | 0 | 51 | 38 | 0 | 0 | 1 | 1 | 20 | 27 | 28 |
| 3 | 88 | 35 | 30 | 24 | 27 | 1 | 17 | 27 | 0 | 1 | 1 | 32 | 0 | 41 | 42 |
| 4 | 118 | 7 | 20 | 32 | 36 | 1 | 43 | 16 | 0 | 1 | 2 | 2 | 40 | 55 | 56 |
| 5 | 147 | 39 | 10 | 40 | 45 | 2 | 9 | 5 | 0 | 2 | 2 | 33 | 21 | 9 | 10 |
| 6 | 177 | 11 | 0 | 48 | 54 | 2 | 34 | 54 | 0 | 2 | 3 | 4 | 1 | 23 | 24 |
| 7 | 206 | 42 | 50 | 57 | 3 | 3 | 0 | 43 | 0 | 2 | 3 | 34 | 41 | 36 | 38 |
| 8 | 236 | 14 | 41 | 5 | 12 | 3 | 26 | 32 | 0 | 3 | 4 | 5 | 21 | 50 | 52 |
| 9 | 265 | 46 | 31 | 13 | 21 | 3 | 52 | 21 | 0 | 3 | 4 | 36 | 2 | 4 | 6 |
| 10 | 295 | 21 | 21 | 21 | 30 | 4 | 18 | 10 | 0 | 3 | 5 | 6 | 42 | 18 | 20 |
| 11 | 324 | 11 | 11 | 29 | 39 | 4 | 43 | 59 | 0 | 4 | 5 | 37 | 22 | 32 | 34 |
| 12 | 354 | 1 | 1 | 37 | 48 | 5 | 9 | 48 | 0 | 4 | 0 | 8 | 2 | 46 | 48 |
| FÜR EINEN HALBEN MONAT ZWISCHEN VOLLMOND UND NEUMOND. | |||||||||||||||
| ½ | 14 | 45 | 55 | 4 | 4½ | 3 | 12 | 54 | 30 | 30 | 3 | 15 | 20 | 6 | 7 |
| BEWEGUNG DER ANOMALIE DER SONNE. | |||||||||||||||
| Monate | Sechzig | Grad | Minuten | Sec. nach Manuscript | Sec. nach Ausgaben | Monate | Sechzig | Grad | Minuten | Sec. nach Manuscript | Sec. nach Ausgaben | ||||
| 1 | 0 | 29 | 6 | 18 | 18 | 7 | 3 | 23 | 44 | 6 | 7 | ||||
| 2 | 0 | 58 | 12 | 36 | 36 | 8 | 3 | 52 | 50 | 24 | 25 | ||||
| 3 | 1 | 27 | 18 | 54 | 54 | 9 | 4 | 21 | 56 | 42 | 43 | ||||
| 4 | 1 | 56 | 25 | 12 | 12 | 10 | 4 | 51 | 3 | 0 | 1 | ||||
| 5 | 2 | 25 | 31 | 30 | 31 | 11 | 5 | 20 | 9 | 19 | 20 | ||||
| 6 | 2 | 54 | 37 | 48 | 49 | 12 | 5 | 49 | 15 | 37 | 38 | ||||
| FÜR EINEN HALBEN MONAT. | |||||||||||||||
| ½ | 0 | 14 | 33 | 9 | 9 | ||||||||||
Wenn wir auf die angegebene Weise die Zeit der mittleren Conjunction oder 0pposition dieser beiden Gestirne, nebst ihrer Bewegung erhalten haben, so ist ihre wahre Distanz, in welcher sie sich einander vorausgehn oder nachfolgen, dazu nöthig, die wahre Conjunction oder Opposition zu finden. Denn wenn der Mond in der Conjunction oder Opposition der Sonne vorausgeht, so ist klar, dass die wahre erst dann eintreten wird, wenn die Sonne die gesuchte wahre bereits passirt hat. Dies ergiebt sich aber aus den beiderseitigen Prosthaphäresen. Wenn nämlich beide Null oder gleich sind, und dabei gleiche Vorzeichen haben, d. h. beide addirt oder beide subtrahirt werden müssen: so treffen offenbar die wahren Conjunctionen oder Oppositionen mit den mittleren in demselben Zeitpunkte zusammen. Wenn sie aber ungleich sind, so ergiebt ihre Differenz selbst den Abstand beider; und zeigt, dass dasjenige Gestirn vorausgeht oder folgt, dessen Prosthaphärese zu addiren oder zu subtrahiren ist. Wenn aber beide verschiedene Vorzeichen haben, so geht dasjenige Gestirn um so mehr voraus, dessen Prosthaphärese abgezogen werden muss, während ihre Summe den Abstand der Gestirne ergiebt. Diesen können wir danach abschätzen, wieviel vom Monde in den ganzen Stunden durchlaufen werden kann, indem wir auf jeden Grad des Abstandes zwei Stunden rechnen. So nehmen wir, wenn zum Beispiel der Abstand ungefähr 6° beträgt, 12 Stunden; zu diesem so bestimmten Zeitintervall suchen wir die wahre Bewegung des Mondes von der Sonne, was leicht auszuführen ist, da wir wissen, dass die mittlere Bewegung des Mondes 1° 1′ in zwei Stunden zurücklegt, dass aber die stündliche und wahre Bewegung der Anomalie bei Voll- und Neumond nahe 50′ beträgt, was in sechs Stunden eine gleichmässige Bewegung von 3° und so vielen Minuten ergiebt, als die wahre Bewegung der Anomalie fünf Grade enthält. Hiermit suchen wir in der Tafel der Mondprosthaphäresen, die Differenz zwischen den Prosthaphäresen, und addiren dieselbe zu der mittleren Bewegung, wenn die Anomalie in dem untern Theile des Kreises, ziehen dieselbe aber ab, wenn sie in dem oberen Theile liegt. Diese Summe oder Differenz ist dann die wahre Bewegung des Mondes in den zu Grunde liegenden Stunden. Diese Bewegung genügt nun, wenn dieselbe der vorher bestehenden Distanz gleich ist; sonst dividiren wir die mit der Anzahl der geschätzten Stunden multiplicirte Distanz durch diese Bewegung, oder dividiren durch die erhaltene wahre stündliche Bewegung die einfache Distanz; und erhalten dann die wahre Differenz der Zeit zwischen der mittleren und wahren Conjunction oder Opposition in Stunden und Minuten. Diese addiren wir zu der mittleren Zeit der Conjunction oder Opposition, wenn der Mond der Sonne voraus ist, oder dem Orte der Sonne diametral gegenübersteht; [249] ziehen sie aber ab, wenn der Mund der Sonne folgt: und so erhalten wir die Zeit der wahren Conjunction oder Opposition. Obgleich wir zugestehen müssen, dass die Ungleichmässigkeit der Sonne hierin noch etwas ändert, so ist dies doch mit Recht zu vernachlässigen, da dies in dem ganzen Verlaufe, und zwar bei der grössten Entfernung, welche sich über sieben Grad erstreckt, nicht eine Minute betragen kann. Es ist daher diese Methode, die Lunationen zu bestimmen, sicherer als eine andere. Gründet man dieselbe nämlich nur auf die stündliche Bewegung des Mondes, welche man den stündlichen Ueberschuss nennt: so täuscht man sich zuweilen, und ist öfter genöthigt, die Rechnung zu wiederholen; denn die stündliche Bewegung des Mondes ist veränderlich und bleibt sich nicht gleich. Für die Zeit der wahren Conjunction oder Opposition berechnen wir auch die wahre Bewegung der Breite, um die Breite des Mondes zu erfahren; und auch den wahren Ort der Sonne vom Frühlingsnachtgleichenpunkte in der Ekliptik, um daraus zu erkennen, ob der Mond in Conjunction oder Opposition steht: und da die so gefundene Zeit mittlere und gleichmässige Krakauer Zeit ist: so reduciren wir dieselbe in der früher angegebenen Weise auf wahre Zeit. Wenn wir dies dann auf andere Orte als Krakau übertragen wollen, so berücksichtigen wir deren Länge, nehmen für jeden Grad dieser Länge 4 Minuten Zeit, für jede Minute der Länge 4 Secunden Zeit, und addiren dies zu der Krakauer Zeit, wenn der Ort östlich, ziehen es aber davon ab, wenn der Ort westlich liegt; und diese Summe oder Differenz ist dann die Zeit der Conjunction oder Opposition der Sonne und des Mondes.
Ob aber Conjunctionen oder Oppositionen mit Verfinsterungen verknüpft sind oder nicht, wird beim Monde leicht erkannt. Wenn nämlich seine Breite kleiner ist, als die Summe der Halbmesser des Mondes und des Schattens, so tritt eine Mondfinsterniss ein; ist sie grösser: so tritt eine solche nicht ein. Aber bei der Sonne hat dies mehr Schwierigkeit, indem dabei die beiderseitigen Parallaxen von Einfluss sind, wodurch sich eine sichtbare Conjunction meistentheils von einer wahren unterscheidet. Wenn wir daher für die Zeit der wahren Conjunction selbst, und für den Zeitraum von einer Stunde vor der wahren Conjunction im östlichen, und nach derselben im westlichen Quadranten der Ekliptik, die Längenparallaxe zwischen Sonne und Mond berechnet haben: so suchen wir die scheinbare Länge des Mondes von der Sonne, um zu erfahren, um wie viel sich der Mond in der Erscheinung von der Sonne in einer Stunde entfernt. Wenn wir mit dieser stündlichen Bewegung in jene Längenparallaxe dividiren: so erhalten wir die Zeitdifferenz [250] zwischen der wahren und scheinbaren Conjunction. Wird diese im östlichen Quadranten der Ekliptik von der wahren Zeit der Conjunction abgezogen, im westlichen zu derselben addirt (denn hier geht die scheinbare Conjunction der wahren voraus, dort folgt sie ihr nach), so erhält man die verlangte Zeit der erscheinenden Conjunction. Für diese Zeit berechnen wir nun, durch die dargelegte Parallaxe der Sonne, die scheinbare Breite des Mondes von der Sonne, oder den Abstand der Mittelpunkte der Sonne und des Mondes bei der scheinbaren Conjunction. Ist diese Breite grösser als die halbe Summe der Durchmesser von Sonne und Mond, so tritt keine Sonnenfinsterniss ein; ist sie aber kleiner, so ereignet sich eine solche. Und hieraus ergiebt sich, dass, wenn der Mond zur Zeit der wahren Conjunction keine Längenparallaxe hat, die scheinbare mit der wahren Conjunction zusammenfällt. Dies geschieht im 90sten Grade der Ekliptik von Osten oder Westen genommen.
Nachdem wir eine Sonnen- oder Mondfinsterniss erkannt haben, finden wir leicht, wie gross dieselbe sein wird; bei der Sonne nämlich aus dem erscheinenden Breitenunterschiede, welcher zur Zeit der scheinbaren Conjunction zwischen Sonne und Mond besteht. Denn wenn wir denselben von der halben Summe der Sonnen- und Monddurchmesser abziehen, so erhalten wir als Rest dasjenige, was von der Sonne, im Durchmesser gerechnet, verfinstert wird. Multipliciren wir dies mit 12, und dividiren das Product durch den Sonnendurchmesser, so erhalten wir die Anzahl der verfinsterten Zolle. Wenn zwischen Sonne und Mond kein Breitenunterschied besteht, so wird die Sonne total oder so viel verfinstert, als der Mond bedecken kann. Ungefähr ebenso verfahren wir bei der Mondfinsterniss, nur dass wir an Stelle des scheinbaren Breitenunterschiedes, die einfache Breite anwenden. Nachdem dieselbe von der halben Summe des Schatten- und Monddurchmessers abgezogen worden ist, bleibt als Rest der verfinsterte Theil des Mondes; wenn nämlich die Breite des Mondes nicht kleiner ist, als der Quotient aus dem Durchmesser des Mondes durch die halbe Summe der Durchmesser; denn alsdann wird der Mond total verfinstert; und eine kleinere Breite ergiebt noch dazu irgend eine Dauer der Finsterniss, welche dann am grössten sein wird, wenn die Breite Null ist, was, wie ich glaube, bei einiger Ueberlegung vollkommen klar sein wird. Wenn wir aber bei einer partialen Mondfinsterniss den verfinsterten Theil mit 12 multipliciren, und das Product durch den Durchmesser des Mondes dividiren, so erhalten wir die Anzahl der verfinsterten Zolle, ganz so wie bei der Sonnenfinsterniss gesagt ist.
[251]


[253] und in solchen Theilen ausgedrückt, in welchen ihre Durchmesser, oder und gegeben sind; und die Inhalte mal und mal ebenfalls, welche gleich sind den Sectoren und . Aber auch die den gleichschenkligen Dreiecken und gemeinschaftliche Basis , und die Lothe und sind gegeben, folglich auch die Produkte mal , als Flächeninhalt des Dreieckes , und mal , als derjenige des Dreiecks . Zieht man nun jedes dieser Dreiecke von seinem Sector ab, so bleiben die Segmente und , aus denen die verlangte Summe sich ergiebt. Auch die Flächeninhalte der ganzen Kreise sind gegeben, bei der Sonnenfinsterniss durch das Product mal , bei der Mondfinsterniss durch das Product mal . Hieraus folgt denn auch, wie viele Zwölftel von dem ganzen Kreise der Sonne oder des Mondes jener verfinsterte Theil ausmacht. — Dies mag nun in Bezug auf den Mond genügen, was bei Anderen weitläufiger abgehandelt ist. Wir eilen zu den Kreisbewegungen der übrigen fünf Gestirne, von denen in den folgenden Büchern die Rede ist.
Anmerkungen [des Übersetzers]
- ↑ [36] 238) Buch III. Cap. 15.
- ↑ [36] 239) Almagest V. 2.
- ↑ [36] 240) Z. B. von Censorinus, vergl. Ideler, Handbuch I. pag. 301 und 352.
- ↑ [36] 241) Vergl. Almagest IV. 2 und 3. Die Ausrechnung von ergiebt auch 29d 31I 50II 8III 9IV 20V 12VI 22VII 26VIII.
- ↑ [36] 242) Mit der Zeit von einem Monate, d. h. nach der Anm. 241) mit , in 360° dividirt giebt ° oder 12° 11′ 26″ 41‴ 24⁗ 42V 5VI. Die Angabe des Textes findet sich im Almagest IV. 3, und scheint ohne Nachrechnung von Copernicus aufgenommen zu sein.
- ↑ [36] 243) Multiplicirt man 12° 11′ 26″ 41‴ 24⁗ 42V 5VI mit 365, so erhält man 12c 126° 37′ 21″ 55‴ 16⁗ 0V 25VI. Will man einen andern Weg einschlagen, so kann man so schliessen, in 345a 82d 1h, d. h. in a werden 4267 360°, d. h. 1536120° zurückgelegt, folglich in einem Jahre oder ° oder 12c 129° 37′ 21″ 55‴ 16⁗ 5V, was [37] mit dem ersten Resultat bis auf 4V 35VI übereinstimmt. Die Angabe des Textes findet sich im Almagest[WS 1] IV. 3 ebenso abweichend.
- ↑ a b [37] 244) Die jährliche Bewegung des Mondes beträgt nach Anm. 243) , multiplicirt man diesen Bruch mit , so erhält man als jährliche Bewegung der Anomalie, und die Ausführung der Division ergiebt
13c 88° 43′ 9″ 9‴ 1⁗ 56V. Man hätte auch so verfahren können, in der Zeit von 345a 82d 1h = legt die Anomalie zurück 4573 360°, folglich in einem Jahre oder was ausdividirt ganz dasselbe Resultat, wie vorhin, ergiebt.
Um die tägliche Bewegung der Anomalie zu berechnen, ist so zu schliessen: in 345a 82d 1h, d. h. in vollendet die Anomalie 4573 360°, also in einem Tage oder = 13° 3′ 53″ 56‴ 34⁗ 21V 4VI.
Multiplicirt man dies wieder mit 365, so erhält man als jährliche Bewegung der Anomalie
13c 88° 43′ 9″ 9‴ 1⁗ 54V 25VI was mit dem ersten Resultate bis auf 1V 35VI stimmt. Die Angaben des Textes finden sich im Almagest IV. 3 ebenso abweichend von der Richtigkeit.
- ↑ [37] 245) Die jährliche Bewegung des Mondes mit multiplicirt giebt oder 13c 148° 42′ 46″ 49‴ 8⁗ und die aus der Säc.-Ausgabe in den Text aufgenommene Angabe stimmt hiermit am besten überein, während die alten Drucke 20‴ statt 49⁗ haben.
Die tägliche Bewegung des Mondes mit multiplicirt giebt = 13° 13′ 45″ 39‴ 45⁗ 3V während alle Ausgaben 40⁗ statt 45⁗ haben.
Multiplicirt man nun das letzte Resultat mit 365, so erhält man
13c 148° 42′ 46″ 49‴ 3⁗ 15V, was mit der Säcular-Ausgabe ganz genau übereinstimmt, aber von den alten Ausgaben um 4⁗ 45V abweicht.a245
- ↑ [37] 245) Die jährliche Bewegung des Mondes mit multiplicirt giebt oder 13c 148° 42′ 46″ 49‴ 8⁗ und die aus der Säc.-Ausgabe in den Text aufgenommene Angabe stimmt hiermit am besten überein, während die alten Drucke 20‴ statt 49⁗ haben.
Die tägliche Bewegung des Mondes mit multiplicirt giebt = 13° 13′ 45″ 39‴ 45⁗ 3V während alle Ausgaben 40⁗ statt 45⁗ haben.
Multiplicirt man nun das letzte Resultat mit 365, so erhält man
13c 148° 42′ 46″ 49‴ 3⁗ 15V, was mit der Säcular-Ausgabe ganz genau übereinstimmt, aber von den alten Ausgaben um 4⁗ 45V abweicht.a245
- ↑ [37] 246)
Almagest IV. 7. wird gesagt, die tägliche Bewegung der Anomalie des Hipparch sei zu verkleinern um 0° 0′ 0″ 0‴ 11⁗ 46V 39VI, daraus folgt eine Verkleinerung der jährlichen um 0° 0′ 1″ 11‴ 38⁗ 47V 15VI, wofür im Text 1″ 11‴ 39⁗ gesetzt ist.
- ↑ [37] 247) Die Zahlenangaben dieses Capitels bieten, wegen der verschiedenen Lesarten, leider eine grosse Verwirrung dar, und um in denselben einige Ordnung zu schaffen, habe ich in dem Texte durchweg zunächst die Lesarten der Säc.-Ausg. beibehalten, in dem hier Folgenden aber dieselben durch Nachrechnen geprüft und mit den Lesarten der alten Ausgaben und des Almagests verglichen. Es handelt sich überhaupt um drei Bestimmungen, nämlich um
- 1, die jährliche mittlere Bewegung,
- 2, die jährliche Bewegung der Anomalie und
- 3, die jährliche Bewegung der Breite des Mondes.
1, Die jährliche mittlere Bewegung des Mondes haben Hipparch und Ptolemäus (Almagest IV. 7.) übereinstimmend gefunden, und zwar = 12c 129° 37′ 21″ 28‴ 29⁗ I. Diese Angabe, welche sich auch in allen Ausgaben des Copernicus findet, ist aber nach Anm. 243) gemäss der von Hipparch und Ptolemäus befolgten Methode nicht genau, und lautet vielmehr 12c 129° 37′ 21″ 55‴ 16⁗ 5V II. Copernicus selbst giebt dieselbe in der Säc.-Ausg. zu 12c 129° 37′ 22″ 32‴ 40⁗ III. und in den alten Ausgaben 12c 129° 37′ 22″ 36‴ 25⁗ IV. In den gleich folgenden Tafeln ist in der Säc.-Ausg. die Angabe III., in den alten Ausgaben die Angabe IV. zu Grunde gelegt. Nach einer Notitz des Herrn M. Curtze ist die Angabe IV. in dem Original Mnscpte. unter der letzten Columne der Tafeln von fremder Hand geschrieben.
[38] Die jährliche mittlere Bewegung des Mondes ist hiernach bei Hipparch kleiner, als bei Copernicus, und zwarnach II u. III um 0″ 37‴ 24⁗ „ II u. IV „ 0 41 9 „ I u. III „ 0 3 11 „ I u. IV „ 1 7 56 Die letzte Lesart findet sich in den alten Ausgaben genau, während die Lesart der Säcular-Ausgabe 1 2 49 mit keinem der obigen Resultate übereinstimmt, und doch ist grade diese Angabe im Orig. Mspte. in Worten ausgeschrieben.
2, Die jährliche Bewegung der Anomalie des Mondes hat Hipparch nach Almagest IV. 3
und allen Ausgaben des Copernicus = 13c 88° 43′ 8″ 40‴ 20⁗ V. nach Anm. 244) müsste sie lauten 13c 88° 43′ 9″ 9‴ 1⁗ 54V 25VI VI. Ptolemäus fand dieselbe (Almagest IV. 7.) = 13c 88° 43′ 7″ 28‴ 41⁗ 13V 55VI VII. Copernicus’ Angabe nach der Säc.-Ausgabe ist 13c 88° 43′ 9″ 5‴ 9⁗ VIII. nach den alten Ausgaben 13c 88° 43′ 9″ 7‴ 15⁗ IX. In den gleich folgenden Tafeln ist in der Säcular-Ausgabe die Angabe VIII, in den alten Ausgaben die Angabe IX zu Grunde gelegt, auch hier sind nach Herrn M. Curtze’s Angabe die Aenderungen des Orig. Mspts. nicht[WS 2] von Copernicus’ Hand.
Hiernach ist die jährliche Bewegung der Anomalie des Mondes bei Hipparch grösser, als bei Ptolemäus
nach VI u. VII um 1° 40″ 20‴ 40V „ V u. VII „ 1 11 38 46 für diese letztere Angabe haben alle Ausgaben des Copernicus 1 11 39 Ferner ist die jährliche Bewegung der Anomalie des Mondes bei Hipparch kleiner, als bei Copernicus
nach V u. VIII um 24‴ 49⁗, wie die Säc.-Ausg. liest, „ V u. IX „ 26 55, wofür die alten Ausgaben 26 56 haben. Die in Anm. 244) berechnete jährliche Bewegung der Anomalie würde ergeben, dass dieselbe bei Hipparch grösser als bei Copernicus gewesen wäre, was mit den Worten des Copernicus nicht zu vereinigen ist.
3, Die jährliche Bewegung der Breite des Mondes hat Hipparch nach Anm. 245) und nach
der Säcular-Ausgabe = 13c 148° 42′ 46″ 49‴ 3⁗ X. nach den alten Ausgaben = 13 148 42 46 20 3 XI. Ptolemäus = 13 148 42 47 12 44 25V 5VI XII. Copernicus nach allen Ausgaben = 13 148 42 45 17 21 XIII. Hiernach ist die jährliche Bewegung der Breite bei Hipparch kleiner als bei Ptolemäus
nach XII u. X um 23‴ 41⁗, die Säcular-Ausgabe hat dagegen 53‴ 41⁗, welche Lesart dadurch entstanden sein kann, dass in Hipparch’s Angabe X 19‴ statt 49‴ gelesen ist; nach XII u. XI um 52‴ 41⁗, was mit den alten Ausgaben genau stimmt. Ferner ist die jährliche Bewegung der Breite bei Hipparch grösser als bei Copernicus
nach XI u. XIII um 1″ 2‴ 42⁗, was mit den alten Ausgaben genau stimmt, „ X u. XIII „ 1″ 31‴ 42⁗, die Säcular-Ausgabe hat dagegen 1″ 1‴ 42⁗, welche Lesart wiederum dadurch sich aufklärt, wenn man annimmt, dass in Hipparch’s Angabe X. 19‴ statt 49‴ gelesen ist.
Woher aber auch in den Tafeln über die jährliche Breite die verschiedenen zu Grunde gelegten Angaben herrühren, lässt sich nicht entdecken, da alle Ausgaben mit der Säcular-Ausgabe in der Angabe XIII. am Schlusse des Capitels 4 übereinstimmen.
- ↑ [38] 248) Almagest IV. 6.
- ↑ [38] 249) Nach dem Regentencanon fangen die Jahre Hadrian’s 863 ägyptische Jahre nach der Nabonassarischen Aera, oder 439 ägyptische Jahre nach dem Tode Alexander’s an. Das Ptolemäische Datum der Mondfinsterniss, nämlich das 17te Jahr Hadrian’s den 20sten Payni, giebt 16 ägyptische Jahre und 289 Tage nach Hadrian’s Regierungsantritt, also hat man
879 äg. Jahre 289d nach Nabonassar oder 455a 289d nach Alexanders Tode davon ab die Schalttage 220 114 bleiben 879 röm. Jahre 69d 455a 175d Christi Geburt 746 308 323 49 bleiben 132a 126d 132a 126d nach Christi Geburt, d. h. im Jahre 133 n. Chr. den 6ten Mai, wie im Texte.
- ↑ [38] 250)
45m mittlere Zeit vor Mitternacht sind 23h 15m 0s mittlere Alexandriner Zeit, Differenz von Alexandrien und Krakau 0 38 36 folglich 22h 36m 24s mittlere Krakauer Zeit, Differenz von Krakau und Frauenburg 0 1 10 folglich 22h 35m 14s mittlere Frauenburger Zeit. - ↑ [39] 251) Muss heissen ♉︎ 13° 15′, wie auch nach der Anm. der Säcular-Ausgabe zu pag. 246 lin. 23 sich in einigen alten Ausgaben finden soll; die Baseler Ausgabe hat dieselbe Lesart wie die Säcular-Ausgabe. Im Almagest steht ♉︎ 13° 14′.
- ↑ [39] 252) Jene 132 römische Jahre und 126d aus Anm. 249) sind, um 33 Schalttage vermehrt, 132 ägypt. Jahre und 159d, danach ergiebt sich
die einfache gleichmässige Bewegung der Sonne und gleichmässige Bewegung der Präcession
für 260a 239° 38′ 14″ 1° 40′ 24″ 12a 356° 57′ 49″ 24‴ 0 10 2 25 260d 118 16 22 0 0 16 38d 37 27 11 11 0 0 5 13 89/96d 0 54 49 27 0 0 0 7 Ort Christi 272 30 5 32 1115 44 26 2 7 22 47 45 oder 3c 35 44 26 2 0 46 6 36 47 45 6 36 47 45 42° 21′ 13″ 47‴ = ♉︎ 12° 21′ wie im Text. - ↑ [39] 253) Das Datum dieser Finsterniss fällt 18 ägypt. Jahre und 91 Tage nach dem Regierungsantritte Hadrians,
also 881 ägypt. Jahre 91 Tage nach Nabonassar oder 457 äg. J. 91d nach Alexander davon ab an Schalttagen 220 114 bleiben 880 röm. Jahre 236 456 r. J. 342 Christi Geb. 746 308 323 49 bleiben 133 „ „ 293 133 „ „ 293 n. Chr. d. h. im Jahre 134 nach Chr. am 20ten October, übereinstimmend mit dem Texte.
- ↑ [39] 254)
1h vor Mitternacht ist 23h 0m 0s mittlere Alexandriner Zeit Differenz für Krakau 0 38 36 ergiebt 22h 21m 24s mittlere Krakauer Zeit, Copernicus rechnet die Differenz für Krakau stets zu 1h, und deshalb steht im Texte 22h.
- ↑ [39] 255) Jene 133 röm. Jahre 293d aus Anm. 262) sind 133 ägypt. Jahre und 326d, dafür ist
Glchmäss. Bew. d. Sonne Glchmäs. Präcession Einfach Anomalie 260a 329° 38′ 14″ 1° 40′ 24″ 12° 34′ 48″ 13a 356° 42 38 31 0 10 52 37 1 21 46 13 560d 295° 40 56 0 0 41 0 5 10 25d 24° 38 24 44 0 0 3 26 0 0 25 50 11/12d 0° 54 12 30 0 0 0 7 0 0 0 57 Ort Christi 272° 30 5 32 6 45 zusammen 1281° 4′ 25″ 45‴ 7° 24′ 1″ 10‴ 20° 47′ 11″ 0‴ oder 3c 200° 4′ 25″ 45‴ doppelt 6° 38 1 10‴ 0° 46 41° 34′ 22″ 6° 38′ 1″ 10‴ 206° 42′ 26″ 55‴ d. h. ♎︎26° 42′ 26″ 55‴, wofür im Texte 26° 43′ steht. - ↑ [39] 256) Das Datum der dritten Finsterniss giebt 19 ägypt. Jahre und 229d nach dem Regierungsantritte Hadrian’s
also 882 ägypt. Jahre 229d nach Nabonassar oder 458 äg. J. 229d nach Alexander davon ab Schalttage 220 114 bleiben 882 röm. Jahre 9d 458 r. J. 115d Christi Geb. 746 308 323 49 bleiben 135 „ „ 66d 135 „ „ 66d nach Chr., d. h. im Jahre 136 nach Chr. am 7ten März, was mit der Textangabe übereinstimmt.
- ↑ [39] 257)
4h nach Mitternacht ist 16h 0m 0s mittlere Alexandriner Zeit Differenz von Krakau 0 38 36 folglich 15h 21m 24s mittlere Krakauer Zeit, Copernicus rechnet die Differenz für Krakau stets zu 1h, und deshalb steht im Texte 15h.
- ↑ [39] 258) Jene 135 röm. J. 66d aus Anm. 265) sind 135 ägypt. Jahre 99d, dafür berechnet sich die einfache gleichmässige Bewegung der Sonne wie folgt: [40] 258)
2 60a 329° 38′ 14″ 15a 356 12 16 46 1 60d 59 8 11 22 38d 37 27 11 11 1/8d 0 7 23 31 Ort Christi 272 30 zusammen 1055° 3′ 16″ 50‴ oder 2c 335° 3′ 16″ 50‴ [WS 4] die corr. Präcession 6 38 0 30 zusammen 341° 41′ 17″ 20‴ [WS 5] oder ♓︎ 11° 41′, wofür im Texte 11° 44′ steht.
- ↑ [40] 259)
Die Sonne stand bei der ersten Finsterniss ♉︎ 13° 15′ vergl. Anm. 251) = 43° 15′ „ „ zweiten „ ♎︎ 25° 10′ = 205 10 Differenz = 161° 55′ wie im Text steht.
- ↑ [40] 260)
Bei der zweiten Finsterniss stand die Sonne ♎︎ 25° 10′ = 205° 10′ „ „ dritten „ „ „ „ ♓︎ 14° 5′ = 344 5 Differenz = 138° 55′, wie in der Säcular-Ausgabe gelesen wird.
- ↑ [40] 261)
Die erste Finsterniss fand statt 132 ägypt. Jahre 158d 23h 15m n. Chr. Alex. Zeit „ zweite „ „ „ 133 „ „ 325 23 0 „ „ „ „ Differenz 1 ägypt. Jahr 166d 23h 45m, was mit dem Text übereinstimmt.
- ↑ [40] 262)
235/8 Stunden sind = 23h 37m 30s, im Almagest IV. 6 ist diese mittlere Zeit zu 23h 39m angegeben. - ↑ [40] 263)
Die zweite Finsterniss fand statt 133 äg. J. 325d 23h n. Chr. Alexandr. Zeit „ dritte „ „ „ 135 „ „ 98d 4h „ „ „ „ Differenz 1 äg. J. 137d 5h mit dem Text übereinstimmend.
- ↑ [40] 264) Diese Angabe stimmt mit derjenigen des Almagest’s a. a. O. überein.
- ↑ [40] 265)
Bewegung des Mondes Einfache Bewegung der Sonne für 1a 129° 37′ 22″ 36‴ 359° 44′ 49″ 7‴ 2 60d 22 53 23 118 16 22 46d 200 46 27 49 45 20 16 42 235/8h 12 0 0 57 0 58 12 44 zusammen 1c 5° 17′ 14″ 22‴ 1c 164° 19′ 40″ 33‴ 164 19 40 33 zusammen 169° 36′ 54″ 55‴, wofür im Text 169° 37′ - ↑ [40] 266)
Anomalie des Mondes für 1a 88° 43′ 9″ 7‴ 2 60d 127 47 53 46d 240 59 21 19 235/8h 12 51 39 1 zusammen 1c 110° 22′ 2″ 27‴, wofür im Text 110° 21′ - ↑ [40] 267)
Bewegung des Mondes Einfache Bewegung der Sonne für 1a 129° 37′ 22″ 36‴ 359° 44′ 49″ 7‴ 2 60d 22 53 23 118 16 22 17d 207 14 33 45 16 45 19 13 51/2h 2 47 37 22 0 13 33 7 zusammen 1c 2° 32′ 56″ 43‴ 1c 135° 0′ 3″ 27‴ 135 0 3 27 zusammen 137° 33′ 0″ 10‴, was mit dem Text genau übereinstimmt. - ↑ [41] 268)
Anomalie des Mondes für 1a 88° 43′ 9″ 7‴ 2 60d 127 47 53 17d 222 6 17 0 51/2h 2 59 38 37 zusammen 1c 81° 36′ 57″ 44‴, wofür im Text 81° 36′ - ↑ [41] 269)
Aus Anm. 259) hat man 161° 55′ aus Anm. 265) „ „ 169 37 Differenz 7° 42′ übereinstimmend mit dem Texte. - ↑ [41] 270)
Aus Anm. 260) hat man 138° 55′ aus Anm. 267) „ „ 137 33 Differenz 1° 22′ mit dem Texte und Almagest IV. 6. übereinstimmend. Die Säc.-Ausg. liest freilich 1° 21′, welche Lesart wir der Folgenden wegen beibehalten wollen. Aus den Anmerkungen 259) bis 270) geht nun unzweifelhaft hervor, dass die Stellung der Sonne bei der ersten Finsterniss ♉︎ 13° 15′ oder 43° 15′, wie dieselbe im Almagest a. a. O. angegeben, wirklich gewesen ist; ebenso dass die Lesart der Säc.-Ausg. bei Anm. 260) die richtige und die um 1° kleinere der alten Ausgaben falsch ist.
- ↑ [41] 271) In der griechischen Ausgabe von Euklids Elementen 1533 und in der lateinischen 1546. Basel, Heruagius ist der hier angewendete Satz der 35ste, während die Säc.-Ausg. denselben als den 30sten bezeichnet. Diese Abweichung könnte ihren Grund darin haben, dass, wie Herr M. Curtze in den Reliqu. Cop. gezeigt hat, Copernicus die Sätze des Euklid nach der Ausgabe des Commandin Venetiis. 1482 citirt; — obgleich ähnliche Abweichungen von den Nummern der Sätze sonst nicht vorkommen.
- ↑ [41] 272)
Es ist nämlich = = = = folglich = - ↑ [41] 273)
Bei der ersten Finsterniss ist der mittlere Ort der Sonne ♉︎ 12° 21′ oder 42° 21′ und zieht man dies von dem mittleren Orte des Mondes ♏︎ 9° 53′ „ 219° 53′ ab so erhält man, wie im Texte, 177° 32′. - ↑ [41] 274) 334° 47′ ist die Lesart der Säc.-Ausg., während die alten Ausgaben 334° 46′ haben.
Es ist aber die Bewegung des Mondes und die einfache Bewegung der Sonne für 10a 216° 13′ 46″ 4‴ 357° 28′ 11″ 10‴ 5 60d 57 13 27 35 295 40 56 37d 91 3 27 35 36 28 3 0 28 26 42 0 2 17 59 zusammen 1c 4° 59′ 7″ 56‴ 1c 329° 39′ 28″ 9‴ 329 39 28 9 334° 38′ 36″ 5‴, wofür im Text 334° 47′ steht. - ↑ [41] 275) Die Anomalie des Mondes ist
für 10a 167° 11′ 31″ 12‴ 5 60d 319 29 42 30 37d 483 24 15 50 0 30 29 5 zusammen 2c 250° 35′ 58″ 37‴, wofür im Text 250° 36′ steht. - ↑ [41] 276)
1, wahrer Ort der Sonne ♎︎ 22° 25′ = 202° 25′, mittlerer Ort ♎︎ 24° 13′ = 204° 13′ 2, „ „ „ „ ♍︎ 22° 12 = 172 12 „ „ ♍︎ 23 49′ = 173 49 329° 47 329° 36′ 334 47 334 47 5° 5° 11′ - ↑ [42] 277)
Bei der zweiten Finsterniss ist der scheinbare Ort der Sonne ♍︎ 22° 12′ = 172° 12′ „ „ dritten „ „ „ „ „ „ „ ♍︎ 11 21 = 161 21 Differenz 32 = 349° 9′ davon ab 346° 10′ giebt den Rest 2° 59′ was mit dem Texte übereinstimmt.
- ↑ [42] 278)
= 306° 43′ dies vom ganzen Kreise abgezogen giebt = 53° 17′ dies von = 250 36 abgezogen ergiebt = 197° 19′ wie im Text - ↑ [42] 279) Vergl. Buch IV. Cap. 5. Anm. 273).
- ↑ [42] 280)
Ptolemäus’ zweite Finsterniss war im Jahre 134 n. Chr. October 20, 22h wahre Zeit Copernicus’ „ „ „ „ „ 1522 „ „ Septemb. 4, 1h 20m „ „ Diese beiden Zeiten auf ägyptische wahre Zeit reducirt, geben
133a 325d 22h = 21h 45m 6s mittlere Zeit 1522a 263d 1h 20m = 1h 19m 2s.4 „ „ Diff. 1388a 302d 3h 20m = 3h 33m 56s.4 „ „ , wofür im Texte 3h 34m gesetzt ist.
Nach Anm. 254) war aber die Zeit der zweiten Finsterniss des Ptolemäus nach mittlerer Krakauer Zeit22h 21m 24s, und die der zweiten Finsterniss des Copernicus fand statt 1h 19m 2s.4, was eine Differenz von 2h 57m 38s.4[WS 7] ergeben würde. - ↑ [42] 281) Die Säcular-Ausgabe[WS 8] liest hier 28′ und dennoch gleich nachher bei Anm. 283) 26′, was nicht zu vereinigen sein würde, deshalb ist im Texte hier die Lesart der alten Ausgaben 38′ beibehalten.
- ↑ [42] 282) Auch hier musste die Lesart der alten Ausgaben 9° 11′ beibehalten werden, obgleich die Säc.-Ausg. 9° 9′ hat, weil sonst die Differenz 38′ bei Anm. 284), welche sich in der Säc.-Ausg. ebenfalls findet, nicht zu verstehen sein würde.
- ↑ [42] 283)
Hipparch’s und Ptolemäus’ Bewegung des Mondes ist 259° 38′ vergl. Anm. 281) Copernicus’ „ „ „ „ 0° 4′ Differenz 0° 26′ was mit allen Ausgaben stimmt. - ↑ [42] 284)
Ptolemäus’ Anomalie des Mondes ist 9° 11′ vergl. Anm. 282) Copernicus’ „ „ „ „ 9° 49′ Differenz 0° 38′ was mit allen Ausgaben stimmt. - ↑ [42] 285) Die Bewegung des Mondes erhält man aus der Tafel des 4ten Cap. dieses Buches
für 2 60a 15554° 45′ 12″ 13a 245 5 53 53‴ 5 60d 3657 13 27 25d 304 46 7 17 21h 37m = 10 58 48 29 zusammen 54c 332° 49′ 28″ 39‴, was mit dem Texte stimmt. - ↑ [42] 286) Die Anomalie des Mondes beträgt nach den Tafeln
für 2 60a 10646° 18′ 14″ 13a 73 20 58 34 5 60d 3919 29 42 25d 326 35 28 32 11 46 3 12 zusammen 41c 217° 30′ 26″ 18‴, hierfür hat die Baseler Ausgabe 222° 32′, die Säcular-Ausgabe 217° 32′.
- ↑ [42] 287)
Bei der zweiten Finsterniss des Ptolemäus stand der Mond von der Sonne ab 182° 47′ Anm. 273) davon ab die Anm. 285) gefundene Bewegung des Mondes 332 49 giebt 209° 58′, mit dem Texte übereinstimmend. - ↑ [43] 288)
Die Anomalie des Mondes war bei der zweiten Finsterniss des Ptolemäus 64° 38′ IV. 5. davon ab die Anmerkung 286) gefundene Anomalie 217 30 giebt 207° 8′ wofür alle Ausgaben 7′ lesen. - ↑ [43] 289) In allen Ausgaben steht fälschlich 1941/2 Tage. Nach Buch III Cap. 22 und 11 beträgt die Zeit, welche zwischen dem Anfange der Olympiaden und dem Anfange der Jahre Christi liegt,
so ergeben sich 193 Olympiaden, 2 römische Jahre, 1841/2 Tage, was ich trotz aller entgegenstehenden Lesarten in den Text aufgenommen habe.775 ägyptische Jahre 121/2d, zieht man hiervon die erforderlichen Schalttage 193 ab, so erhält man 774 römische Jahre 1841/2d, dividirt man mit 4, - ↑ [43] 290) Vergl. Buch III. Cap. 11.
- ↑ [43] 291) Die Bewegung des Mondes beträgt nach den Tafeln
für 1260a 3328° 31′ 17″ 55a 289 15 43 22 12d 146 17 20 18 6 11 18 35 zusammen 10c 170° 15′ 39″ 15‴ dies von 209 58 ab ergiebt 39° 43′, wofür im Texte 39° 48′ steht. - ↑ [43] 292) Die Anomalie des Mondes beträgt nach den Tafeln
für 1260a 20677° 49′ 27″ 55a 199 33 21 38 12d 156 46 47 18 6 36 1 56 zusammen 58c 160° 45′ 37″ 52‴ dies von 207° 7′ ab ergiebt 46° 21′, was mit dem Texte übereinstimmt. - ↑ [43] 293) Die Bewegung des Mondes beträgt nach den Tafeln
für 560a 17286° 53′ 2″ 23a 101 19 39 57 260d 1462 53 23 10d 121 54 26 55 6 12 19 33 zusammen 52c 259° 12′ 51″ 25‴, dies ab von 209 58 ergiebt 310° 45′, übereinstimmend mit dem Text. - ↑ [43] 294) Die Bewegung der Anomalie des Mondes beträgt
für 560a 5015° 45′ 36″ 23a 240 32 29 46 260d 1567 47 53 10d 130 38 59 25 8 34 46 1 zusammen 19c 123° 19 44 12 dies ab von 207 7 ergiebt 83° 47′, wofür im Text 85° 41′, gelesen wird. - ↑ [44] 295) Die Bewegung des Mondes beträgt
für 45a 73° 1′ 57″ 18‴ 12d 146 17 20 18 zusammen 219° 19′ 17″ 36‴ dies ab von 209° 58 giebt 350° 39′ übereinstimmend mit dem Texte. - ↑ [44] 296) Die Bewegung der Anomalie des Mondes beträgt
für 45a 32° 21′ 50″ 26‴ 12d 156 46 47 18 zusammen 189° 8′ 37″ 44‴ dies ab von 207 7 giebt 17° 58′ übereinstimmend mit dem Texte. - ↑ [44] 297) Epidamnum, später Dyrrhachium, jetzt Durazzo. Die geographischen und astronomischen Bestimmungen der drei im Texte genannten Orte sind folgende:
Namen der Orte östl. Länge von Greenwich Unterschied der Sternzeit Unterschied der mittl. Zeit Durazzo 19° 27′ 15″ 1h 17m 49a 1h 17m 36s,2516 Frauenburg 19 40 7,5 1 18 40,5 1 18m 27a,6109 Krakau 19 57 46,5 1 19 51,1 1 19m 28a,0182 - ↑ [44] 298) Vergl. Almagest V. 3.
- ↑ [44] 299) Vergl. Buch IV. Cap. 5., wo , hier , = 8604, wenn , hier , = 100000. Da nun hier = 10000, so ist = 860,4, also ungefähr 860, wie im Texte steht. In demselben Cap. 5 ist bei der Discussion der Ptolemäischen Finsternisse = 870,6 gefunden.
- ↑ [44] 300) Vergl. Almagest V. 5., wo die Zeit vom Mittag zu Alexandrien 3h 20m gegeben ist, während Hipparch den Tag 6h früher anfängt, und deshalb die Zeit zu 9h 20m rechnen muss.
- ↑ [44] 301) Mit dieser Angabe übereinstimmend liest man im Almagest V. 5. 10° 54′ des Krebses.
- ↑ [44] 302)
10° 54′ ♋︎ sind 100° 54′ der Abstand ☉☽ ist 48 6 zusammen 149° 0′ d. i. 29° ♌︎ - ↑ [44] 303) Die geographische Breite des Molo von Rhodos wird in Rümkers Schifffahrtskunde zu 36° 26′ 53″ angegeben.
- ↑ [44] 304) Aequinoctialstunden sind gleichbedeutend mit unseren gleichmässigen Stunden, d. h. sie betragen je 1/24 des bürgerlichen Tages, und haben ihren Namen davon, dass sie um die Zeit der Nachtgleichen den bürgerlichen Tag- und Nacht-Stunden, horae temporales, gleich sind. Die Aequinoctialstunden, welche bei den Alten ὤραι ἰσημεριναί, oder horae aequinoctiales hiessen, sind mit den heutigen astronomischen Stunden gleichbedeutend; während die ὤραι ϰαιριϰαί, oder horae temporales die jedesmalige Länge des Tages oder der Nacht in zwölf Theile theilten. Letztere verändern sich also mit der geographischen Breite des Ortes und mit den Jahreszeiten; Erstere bleiben für alle Beobachtungsorte und Jahreszeiten sich gleich. Vergl. Ideler, Handbuch I. pag. 86 und 87.
- ↑ [44] 305) Ptolemäus sagt im Almagest V. 5.: „quoniam post meridiem diei 17 Pauni 3.20 horis temporalibus facta observatio fuit, quae tunc in Rhodo quatuor proxime faciebant aequales“ und setzt später hinzu: „simpliciter quidem 4, exacte autem 3.40.“ — Mit diesem Gegensatze von simpliciter und exacte wird die Umwandlung der horae temporales in horae aequinoctiales gemeint. Um diese Umwandlung auszuführen, ist zuerst das Datum der besprochenen Beobachtung auf christliche Zeitrechnung zu reduciren. In Buch III. Cap. 11. und den dortigen Anmerkungen haben wir gesehen, dass verflossen sind
[45] vor Christi Geburt, d. h. im Jahre 127 vor Chr. den 7ten Juli. Der 7te Juli fällt aber 108 Tage nach der Frühlingsnachtgleiche. Da nun vom 21sten März bis zum 21sten September 184 Tage verstrichen, so haben wirvon Alexanders Tode bis Cäsar 278a 118d.5 „ Cäsar „ Augustus 15a 246d.5 „ Augustus „ Christus 29a 130d.5 zusammen 322a 495d.5 römisch oder 323a 130d.5 ägyptisch von Alexanders Tode bis zu dem fraglichen Datum sind verflossen 196a 286d ägyptisch bleiben 126a 209d.5 ägyptisch davon ab die Schalttage 31.5 bleiben 126a 178d römisch 184d : 108d = 180° : ° woraus sich ergiebt: = 105° 39′ 8″ also 180° — = 74° 20′ 52″ 
Ist nun der Aequator, die Ekliptik, das Herbstäquinoctium, so ist der
Bogen oder = 74° 20′ 52″ Winkel = 23" 51′ 20″ und man hat =
= 9.98359 = 9.64563 = 9.62922 woraus = 23° 4′ 53″ also = = 66° 55′ 7″ Wenn ferner das Zenith, [WS 9] der Horizont, der Pol, der Aufgangspunkt des Punktes der vorigen Figur, und der Stundenwinkel ist, so haben wir
= oder = = 66° 55′ 7″ = 36° also = 9.62922 = 9.86126 = 9.49048 = 18° 1′ 17″ = 108° 1′ 17″ Hiernach hat man obige 3h 20m horae temporales in horae aequinoctiales umzuwandeln, indem man setzen muss
90° : 108° 1′ 17″ = 31/3 : woraus sich ergiebt = 4h 0m 2s.851 horae aequinoctiales.
- ↑ [45] 306)
Nach Hipparchs Beobachtung stand ☉ ♋︎ 10° 54′ = 100° 54′ ☾ ♌︎ 29° = 149° also war der beobachtete Abstand zwischen ☉ und ☾ = 48° 6′ der wahre Ort der Sonne war aber ♋︎ 10° 40′ „ „ „ des Mondes ♌︎ 28° 37′ also der wahre Abstand = 47° 57′ Differenz = 0° 9′, wie im Texte. - ↑ [45] 307) Zur Zeit der mittleren Conjunctionen und Oppositionen ist die halbe Sehne des doppelten Winkels , d. h. = 860, wenn der Radius 10000 beträgt, also Winkel = 4° 56′, wie im Text.
- ↑ [45] 308) Der Durchmesser des kleinen Epicykels, also 2, ist nämlich = 2 237 = 474. Dies zu = 860 hinzuaddirt, giebt = 1334. Dies als halbe Sehne des doppelten Winkels genommen, während der Halbmesser 10000 beträgt, ergiebt den Winkel = 7° 40′, davon abgezogen den Winkel = 4° 56′, ergiebt als Rest 2° 44′.
- ↑ [45] 309) Nimmt man 1123 als halbe Sehne des doppelten Winkels, so ist der entsprechende Winkel genau:
6° 26′ 52″.5, wofür im Texte steht 6° 29′, zieht man davon ab 4 56 4 56, so bleibt 1° 30′ 52″.5, „ „ „ „ 1° 33′. - ↑ [45] 310) Berechnet man diese Zahl mittelst der in Anm. 309) gefundenen Differenz, so ergiebt sich 33′,247, statt der 34′ des Textes.
- ↑ a b [45] 311) Vergl. Almagest V. 8.
- ↑ [46] 312) Obgleich in dem nächstfolgenden Capitel 12 ausdrücklich gesagt ist, dass die Breite des Mondes dann nördlich ist, wenn dieselbe auf der ersten Tafel steht, dagegen südlich, wenn sich dieselbe auf der zweiten Tafel findet, liest man in allen Ausgaben in dem Kopfe beider Tafeln „nördliche Breite.“
- ↑ [46] 313) In allen Ausgaben steht zwar „latitudinis“, es giebt dies aber keinen Sinn und muss unzweifelhaft „longitudinis“ heissen.
- ↑ [46] 314) Almagest VI. 5.
- ↑ [46] 315) Almagest a. a. C. hat 163° 40′.
- ↑ [46] 316) Almagest IV. 9.
- ↑ [46] 317) Buch IV. Cap. 5.
- ↑ [46] 318) Die alten Ausgaben haben hier 23° 11′, während im Manuscripte des Copernicus 23° 16′ steht.
- ↑ [46] 319) Vergl. Buch III. Cap. 11.
- ↑ [46] 320) Almagest V. 12.
- ↑ [46] 321) Almagest I. 13.
- ↑ [46] 322) Almagest V. 13.
- ↑ [46] 323) Almagest V. 14.
- ↑ [46] 324)
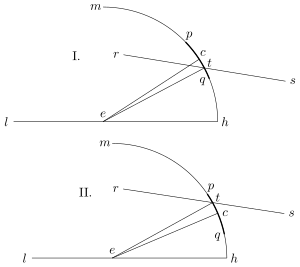
Die Figur I bezieht sich auf die erste der im Texte erwähnten Mondfinsternisse, die Figur II auf die zweite. In beiden Figuren liegen die Linien in der Ekliptik, und bezeichnen also die Axen des Schattens der Erde; die Bogen gehören den durch den Mittelpunkt des Mondes gelegten Längenkreisen an, der Theil derselben bezeichnet den Durchmesser des Mondes = 31′ 20″ = 12 Zoll; ist die in der Ebene des Längenkreises gelegene Grenzlinie des Erdschattens, welche den Monddurchmesser in trifft, während der Mittelpunkt des Mondes ist.
Nun ist der Winkel bei der ersten Finsterniss[WS 11] 47′ 54″, bei der zweiten 29′ 37″ und „ „ „ „ „ „ 7′ 50″, „ „ „ 10′ 27″ Differenz = 40′ 4″, Summa = 40′ 4″, wie im Text.
- ↑ [46] 325) Almagest V. 15.
- ↑ [46] 326) Die Säc.-Ausg. liest hier 60:5859/60, während es nach der kurz vorhergehenden Berechnung heissen muss 60:5649/60. Die Baseler Ausgabe hat 60:5848/60. Die gleich nachfolgende Bestimmung von und lässt über die Richtigkeit der Lesart 5649/60 keinen Zweifel übrig; denn wenn
= 60 : 5649/60 so muss auch = 60 : 5649/60 oder = 60 - 5649/60 : 60 oder = 311/60 : 60 - ↑ [47] 327) Diese Zahl müsste richtiger lauten 253, denn
= 1422/60 : 60 oder 641/6 : = 1422/60 : 60, was für = 252,9 ergiebt. - ↑ [47] 328) Diese Behauptung stützt sich auf das Ende des Cap. 30 des Liher Machometi Geber, qui vocatur Albategni. 1537.
- ↑ [47] 329) Vergl. Buch IV. 17.
- ↑ [47] 330) Zur Uebersicht der Zahlenangaben dieses Capitels diene nachstehendes Täfelchen
Grenzen Entfernung des Mondes in Erdhalbmessern. Horizontalparallaxe des Mondes Scheinbarer Durchmesser des Mondes. Scheinbarer Durchmesser des Schattens. I Grösste Entfernung[WS 12] in der Quadratur 687/20 50′ 18″ 28′ 45″ - II Grösste Entfernung in der Syzygie 651/2 52′ 24″ 30′ od. 29′ 58″ 80′ 36″ III Kleinste Entfernung in der Syzygie 552/15 62′ 21″ 35′ 38″ 95′ 44″ IV Kleinste Entfernung in der Quadratur 5217/60 65′ 45″ 37′ 34″ - - ↑ [47] 331) Vergl. Buch IV. 20.
- ↑ [47] 332) Die Baseler Ausgabe hat hier fälschlich 14′ 8″.
- ↑ [47] 333)
Man hat offenbar 1 : 1142 = : , setzt man nun den Winkel = und = , so ist 1 : 1142 = : = : = 1 : folglich ; setzt man nun = 30°, so ergiebt sich = 1′ 35″, wofür im Text 1′ 30″ steht; setzt man aber = 60°, so ergiebt sich = 2′ 39″, wofür im Text 2′ 36″ steht. - ↑ [47] 334) Diese Parallaxe würde nur für das Apogeum des Mondes gelten, für das Perigeum müsste man dieselbe Correction 4′ 50″ von der zweiten rectificirten Parallaxe des Mondes, also von 51′ 13″[WS 13] abziehen, und man erhielte 46′ 23″ als Parallaxe des Mondes für das Perigeum. Der nun folgende Schluss des Capitels 25 findet sich ausschliesslich in der Säc.-Ausg. und ist dem Manuscripte entnommen.
- ↑ [47] 335) Copernicus will hier offenbar den Stern Tauri, also den Aldebaran, bezeichnen. Der Name Palilicium, — wohl besser Parilicium, auch Parelicium, — umfasst die sämmtlichen Hyaden, wie aus Plinius’ Historia naturalis XVIII. 26 hervorgeht, wo es heisst: „XIV. kalend. Maias Aegypto suculae“, die Hyaden, „occidunt vesperi, sidus vehemens et terra marique turbidum, XVI. Atticae, XV. Caesari, continuo quatriduo significant, Assyriae autem XII. kalend. Mai.; hoc est vulgo appellatum sidus Parilicium, quoniam XI kalend. Majas urbis Romae natalis habetur, quo fere serenitas redditur; claritatem observationi dedit; nimborum argumento hyadas appellantibus Graecis eas stellas, nostri a similitudine cognominis Graeci propter sues inpositum arbitrantes inperitia appellavere suculas.“ Ausg. von Julius Sillig Vol. III. p. 200. — Die Hyaden wurden aber von den Römern Sidus Parilicium genannt, weil sie um den 21sten April, — XI. kalend. Maias, — an welchem Tage das Hirtenfest Parilia oder Palilia, gefeiert wurde, und nach einer alten Tradition Rom gegründet war, — in der Abenddämmerung verschwanden. Siehe Ideler’s Untersuchungen über den Ursprung und die Bedeutung der Sternnamen pag. 140.
- ↑ [47] 336) Dieser Satz findet sich in Ἀρϰιμήδους ϰύϰλου μέτρησις · πρότασις γ' und lautet daselbst: „Παντὸς ϰύϰλου ἡ περίμετρος, τῆς διαμέτρον, τριπλασίων ἐστὶ, ϰαὶ ἔτι ὑπερ έχετ, έλάσσοντ μὲν ἢ ἑβδόμψ μέρει τῆς διαμέτρου, μείζονι δὲ ἢ δέϰα ἑβδoμηϰοστομόνοις.“ Die lateinische Uebersetzung der Oxforder Ausgabe v. 1792 von Torelli lautet folgendermaassen: „Cujuslibet circuli ambitus diametri est triplus, et adhuc parte quadam excedit, quae quidem minor est septima diametri parte, major vero decem septuagesimis primis.“ Vergl. die angeführte Ausgabe Seite 205 und 206.
- ↑ [48] 337) Diese Angabe findet sich im Almagest VI. 7. und nähert sich der gebräuchlichen Ludolfschen Zahl bis auf ungefähr 0,00007, denn sie giebt ausgerechnet 3,141666…, während der Anfang der Ludolfschen Zahl 3,14159265 lautet.
Anmerkungen (Wikisource)
| ← Drittes Buch Teil B | Nach oben | Fünftes Buch Teil A → |
| Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext. |




















































































































































































































































































































































