Wikisource

Seite:NewtonPrincipien.djvu/77

Fertig. Dieser Text wurde zweimal anhand der Quelle korrekturgelesen. Die Schreibweise folgt dem Originaltext.

wie die, auf die grosse Axe als Abscissenaxe bezogenen, Ordinaten, mithin wegen der Gleichheit des directen und des indirecten Verhältnisses, wie

1 : 1.[1]

§. 28. Anmerkung. Wird die Ellipse durch Entfernung ihres Mittelpunktes ins Unendliche in eine Parabel verwandelt, so bewegt sich der Körper auf dieser, und es wird die jetzt nach dem unendlich entfernten Punkt Centrum gerichtete Kraft constant. Dies ist Galilei’s Lehrsatz.

Verwandelt sich der parabolische Schnitt (durch Veränderung der Neigung der schneidenden Ebene) in eine Hyperbel, so bewegt sich der Körper auf dem Umfange der letztern, indem die Centripetalkraft in eine Centrifugalkraft übergeht. Sowie in einem Kreise oder einer Ellipse bei denen die Kräfte nach einem, auf einer Abscisse gelegenen Mittelpunkte der Figur gerichtet sind, diese Kräfte, durch Vergrösserung oder Verkleinerung der Ordinaten in irgend einem gegebenen Verhältniss, oder auch durch Aenderung des Neigungswinkels der Ordinaten gegen die Abscisse, immer im Verhältniss der Entfernungen vom Centrum wachsen oder abnehmen, wenn nur die Umlaufszeiten gleich bleiben; werden in allen Figuren, wenn die Ordinaten in irgend einem Verhältniss zu- oder abnehmen, oder der Coordinatenwinkel bei unveränderter Umlaufszeit irgendwie verändert wird, die nach einem beliebigen, auf einer Abscisse gelegenen Centrum, gerichteten Kräfte in den einzelnen Ordinaten im Verhältniss der Abstände vom Centrum zu- oder abnehmen.

ABSCHNITT III.
Von der Bewegung der Körper in excentrischen Kegelschnitten.

Fig. 24.

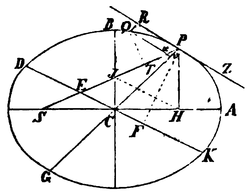
§. 29. Aufgabe. Ein Körper bewegt sich in einer Ellipse; man sucht das Gesetz der nach ihrem Brennpunkt gerichteten Centripetalkraft.

Es sei S der Brennpunkt der Ellipse. Man ziehe SP, welche den Durchmesser DK in E und die Ordinate Qv in x schneidet und vollende das Parallelogramm QxPR. Offenbar ist

EP = AC.
  1. ↑ [580]

    Fig. 228.

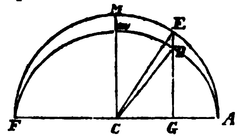
    No. 16. S. 69. Die gemeinschaftliche halbe grosse Axe sei = a, die halbe kleine Axe CM = B, Cm = b, die Umlaufszeiten resp. T und t. Da die beschriebenen Flächenräume den Zeiten proportional sind, haben wir
    1.     T : t = aBπ : abπ = B : b

    Sind nun ACD, ACE gleichzeitig beschriebene Sectoren, so wird die Umlaufszeit desto kleiner, je grösser ein solcher Sector ist; also

    2.     T : t = ACD : ACE.

    Sind diese Sectoren aber sehr klein, so verhalten sie sich wie die Geschwindigkeiten im Punkt A oder nach §. 7.

    3.     ACE : ACD = EG : DG.

    Setzt man nun, der Kürze wegen, AG = x, so hat man , also

    4.     DG : EG = b : B

    oder nach 2., 3. und 4. T : t = b : B, und nach 1. T : t = B: b, also

    5.     T : t = 1 : 1.
Empfohlene Zitierweise:
Isaac Newton: Mathematische Principien der Naturlehre. Robert Oppenheim, Berlin 1872, Seite 69. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/77&oldid=- (Version vom 1.8.2018)
Von „https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/77&oldid=3354965“