Seite:NewtonPrincipien.djvu/588

	Isaac Newton: Mathematische Principien der Naturlehre

No. 14. S. 68. Es wird nämlich Qv² + uP · Pv = Pv (uV + uP) = vP · P · V. Ferner ist uP = PT + Tv; vP = PT – Tv also uP · vP = PT² – Tv² und Qv² + uP · Pv = Qv² – Tv² + PT² = QT² + PT² = PQ².

No. 15. S. 68. Wenn Q mit P zusammenfällt, wird PF mit dem Perpendikel von C auf die Tangente identisch.

Fig. 228.

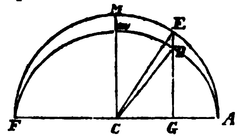
No. 16. S. 69. Die gemeinschaftliche halbe grosse Axe sei = a, die halbe kleine Axe CM = B, Cm = b, die Umlaufszeiten resp. T und t. Da die beschriebenen Flächenräume den Zeiten proportional sind, haben wir

1.     T : t = aBπ : abπ = B : b

Sind nun ACD, ACE gleichzeitig beschriebene Sectoren, so wird die Umlaufszeit desto kleiner, je grösser ein solcher Sector ist; also

2.     T : t = ACD : ACE.

Sind diese Sectoren aber sehr klein, so verhalten sie sich wie die Geschwindigkeiten im Punkt A oder nach §. 7.

3.     ACE : ACD = EG : DG.

Setzt man nun, der Kürze wegen, AG = x, so hat man $\scriptstyle DG^{2}={\frac {b^{2}}{a^{2}}}\left(2ax-x^{2}\right)EG^{2}={\frac {B^{2}}{a^{2}}}\left(2ax-x^{2}\right)$, also

4.     DG : EG = b : B

oder nach 2., 3. und 4. T : t = b : B, und nach 1. T : t = B: b, also

5.     T : t = 1 : 1.

Fig. 229.

No. 17. S. 73. Ist A der Hauptscheitelpunkt der Parabel, S ihr Brennpunkt, P ein anderer Scheitelpunkt, x' die Abscisse, y' die Ordinate, beide auf den letzteren Scheitelpunkt bezogen; so hat man bekanntlich $\scriptstyle y'^{2}={\frac {2p}{\sin \ \alpha ^{2}}}x'$. Es ist aber $\scriptstyle tg\alpha ={\frac {p}{b}}$, also $\scriptstyle {\frac {2p}{\sin \ \alpha ^{2}}}=2p\cdot {\frac {b^{2}+p^{2}}{p^{2}}}={\frac {2p\left(2ap+p^{2}\right)}{p^{2}}}=4\left(a+{\frac {p}{2}}\right)$ und da $\scriptstyle r^{2}=b^{2}+\left({\frac {p}{2}}-a\right)^{2}=2ap+{\frac {p^{2}}{4}}-pa+a^{2}=\left(a+{\frac {p}{2}}\right)^{2}$ also $\scriptstyle r=a+{\frac {p}{2}}$, so wird $\scriptstyle {\frac {2p}{\sin \ \alpha ^{2}}}=4r$.

No. 18. S. 73. Ist wie vorhin PO = b, AO = a (Fig. 26.), so wird als Subtangente $\scriptstyle MO={\frac {b}{tga}}={\frac {b^{2}}{p}}={\frac {2ap}{p}}=2a$, mithin MA = AO = a. Ferner ist SP = r = a + $\scriptstyle {\frac {p}{2}}$ = AM + AS = MS, endlich da MSP gleichschenklig und SN (Fig. 26.) perpendikular auf MP, so ist MN = NP.

Empfohlene Zitierweise:
Isaac Newton: Mathematische Principien der Naturlehre. Robert Oppenheim, Berlin 1872, Seite 580. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/588&oldid=- (Version vom 1.8.2018)