Seite:NewtonPrincipien.djvu/57

	Isaac Newton: Mathematische Principien der Naturlehre

Es ist nämlich nach Vollendung des Parallelogrammes AFBD

BF = AD.^{[WS 1]}

Zusatz 2. Werden durch B und A beliebige gerade Linien BD, BE, AF, AG gezogen, welche die Tangente AD und die ihr parallele Linie BF in den Punkten D, E, F, G schneiden; so wird das letzte Verhältniss aller Abscissen AD, AE, BF, BG, der Sehne AB und des Bogens ACB das der Gleichheit.

Zusatz 3. Daher kann bei jedem die letzten Verhältnisse betreffenden Beweise, jede dieser Linien gegenseitig statt der andern gesetzt werden.

Fig. 11.

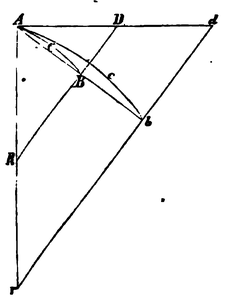
§. 8. Lehnsatz. Bilden die gegebenen geraden Linien AB und BR mit dem Bogen ACB, der Sehne AB und der Tangente AD die Dreiecke

ACBR, ABR, ADR,

und nähern sich die Punkte A und B einander gegenseitig; so wird die letzte Form dieser einander ähnlich und ihr letztes Verhältniss das der Gleichheit.

Man verlängere AB, AD, AR bis b, d, r, ziehe

rbd ∥ RBD

und

$\scriptstyle \frown$ Acb ∼ ACB.

Fig. 12.

Fallen nun die Punkte A und B zusammen, so verschwindet der Winkel bAd, es fallen daher die Dreiecke

Acbr, Abr, Adr

zusammen, und sind einander congruent; folglich werden auch die ihnen ähnlichen Dreiecke

ACBR, ABR, ADR

einander congruent.     W. z. b. w.

Zusatz. Diese Dreiecke können mithin überall, wo es sich hier um ihre letzten Verhältnisse handelt, statt einander gesetzt werden.

§. 9. Lehnsatz. Die ihrer Lage nach gegebene Curve ABC und gerade Linie AE schneiden sich im Punkte A, und zu den Abcissen AD, AE gehören die Ordinaten DB, EC. Lässt man nun die Punkte B und C dem A sich nähern, so stehen die Dreiecke ADB und AEC zuletzt im doppelten Verhältniss der Seiten.

Anmerkungen (Wikisource)

1. Vorlage: BF = BD

Empfohlene Zitierweise:
Isaac Newton: Mathematische Principien der Naturlehre. Robert Oppenheim, Berlin 1872, Seite 49. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/57&oldid=- (Version vom 14.3.2018)