Mathematische Principien der Naturlehre/Bemerkungen und Erläuterungen
| ← Ueber das Weltsystem. | Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Bemerkungen und Erläuterungen |
No. 1. S. 40. (Dortige Figur). RV drückt die ganze Verzögerung aus, welche das Pendel durch den Widerstand der Luft erleidet, während es eine doppelte Schwingung ausführt; dieselbe widerstehende Kraft würde daher ½RV hervorbringen, während das Pendel eine einfache Schwingung zurücklegt. Der Anfangspunkt der letzteren ist aber weder in R noch in V, sondern in irgend einen zwischen beiden liegenden Punkt zu setzen, weil der Körper eine grössere Verzögerung erlitten hat, während er den grösseren Bogen der ersten, als während er den kleineren Bogen der zweiten Schwingung beschrieb. Dieser zwischenliegende Punkt wird genähert erhalten, wenn man ST = ¼RV so in die Mitte legt, dass der Punkt x sowohl ST als RV halbirt.
No. 2. S. 52. Setzt man den Bogen AB = α, Ab = β, so wird für den Radius AM = 1, BD = AC = sin vers. α = 1 – cos. α = 2 sin ½α² AB = 2 sin AGB = 2 sin ½α und eben so bd = 2 sin ½β²; Ab = 2 sin ½β. Werden nun α und β verschwindend klein, so wird BD = ½α², AB = α, bd = ½β², Ab = β, demnach jetzt: AB² : Ab² = α² : β² = BD : bd.
No. 3. S. 52. Weil , so wird AD² = Constans. DB, und daher für AC = DB als Abscisse, BC = AD die zugehörige Ordinate in einer Parabel. Ferner ist nach den Gesetzen der Parabel die krummlinige Figur ABC = ⅔ ACBD und daher die krummlinige Figur ABD = ⅓ ABCD = ⅔ Δ ABD.
No. 4. S. 56. (Dortige Figur). Da nämlich CV ∥ AB und Cc ∥ BV, so ist CVBc ein Parallelogramm, also CV = Bc = AB, und da auch CV ∥ AB, so wird ABCV ebenfalls ein Parallelogramm, dessen Diagonale BV nach der Construction den Mittelpunkt S trifft.
No. 5. S. 57. Da AB = BG ist, hat man Δ SAB = SBc. Nach der Voraussetzung ist SAB = SBC, also SBC = SBc, mithin Cc ∥ SB. Längs BS muss auch die Centripetalkraft gerichtet sein, welche bewirken soll, dass der Körper, statt von B längs Bc fortzugehen, nach C hin abgesenkt werde.
No. 6. S. 59. Setzt man die Umlaufszeiten in zwei Kreisen = T, t, die Radien = R, r; so würden die in der Zeiteinheit beschriebenen Bogen , . Das in §. 18. enthaltene Verhältniss geht daher über .
No. 7. S. 60. Werden die Centripetalkräfte durch F, f, die Geschwindigkeiten durch V, v bezeichnet; so ist nach dem Lehrsatz und nach Zusatz 2. und da hier T²:t² = R³:r³; so wird . Ferner geht die Proportion hier über in .
No. 8. S. 60. Setzt man allgemein die Schwerkraft = 2g, so wird bekanntlich ein vermöge derselben beschriebener Weg f = gt³. Setzt man nun die Zeit t = 1, und wird während derselben Zeit der Bogen a des Kreises beschrieben, so gehört zu demselben die Fallhöhe g und es ist daher g · 2r = a² oder 2g = , d. h. die Schwerkraft identisch mit der Centripetalkraft. Demnach und für t = 1 a² = 2r · f.
No. 9. S. 61. Bezeichnet Pp die Geschwindigkeit in P, Qq die Geschwindigkeit in q, wobei die kleinen Stücke Pp und Qq der Tangenten statt der Bogen gesetzt sind; sind ferner SM und SN die Perpendikel auf die Tangente: so ist Fläche SPp = ½Pp · SM, Fläche SQq = ½Qq · SN, also SPp : SQq = Pp · SM : Qq · SN. Nach §. 13. sind aber SPp und SQq den Zeiten proportional, und im vorliegenden Falle einander gleich und mit der Zeiteinheit identisch. Daher Pp · SM = Qq · SN oder Pp : Qq = SN : SM. Nach der Construction ist Pp : Qq = QB : AP = DQ' : DP' (Fig. 17). Angenommen nun, die Linie TS träfe DP' nicht in D, sondern in einem am x davon entfernten Punkte F; so denke man sich ein Perpendikel FG auf TN gefällt. Es würde dann leicht folgen SM : DP' + x = SN : FG und da oben SM : DF = SN : DQ' jetzt DP' + x : DP' = FG : DQ'. Dies ist aber nicht möglich, weil DP' + x > DP' und FG < DQ; es muss daher TS durch D gehen.No. 10. S. 62. Die Centripetalkraft verhält sich daher (nach §. 21.) direct wie und indirect wie der Körper .
No. 11. S. 63. Eigentlich hat man, wenn PR eine Tangente in P ist, VP : PR = PQ : PR und daher . Ist aber der Bogen PQ verschwindend klein, so wird QR ∥ VP, PR = PQ = PQ und so .No. 12. S. 67. Sind in der Ellipse oder Hyperbel a' und b' conjugirte Halbmesser, α der Coordinatenwinkel, a und b die halben Hauptaxen, so ist bekanntlich a'b' sin α = ab.
No. 13. S. 67. Setzt man Pv = x', Qv = y', DC = b', CP = a', so stimmt die Proportion Pv · vG : Qv² = PC² : CD² (Fig. 23.) mit der bekannten Gleichung der Ellipse überein. No. 14. S. 68. Es wird nämlich Qv² + uP · Pv = Pv (uV + uP) = vP · P · V. Ferner ist uP = PT + Tv; vP = PT – Tv also uP · vP = PT² – Tv² und Qv² + uP · Pv = Qv² – Tv² + PT² = QT² + PT² = PQ².
No. 15. S. 68. Wenn Q mit P zusammenfällt, wird PF mit dem Perpendikel von C auf die Tangente identisch.
No. 16. S. 69. Die gemeinschaftliche halbe grosse Axe sei = a, die halbe kleine Axe CM = B, Cm = b, die Umlaufszeiten resp. T und t. Da die beschriebenen Flächenräume den Zeiten proportional sind, haben wirSind nun ACD, ACE gleichzeitig beschriebene Sectoren, so wird die Umlaufszeit desto kleiner, je grösser ein solcher Sector ist; also
Sind diese Sectoren aber sehr klein, so verhalten sie sich wie die Geschwindigkeiten im Punkt A oder nach §. 7.
Setzt man nun, der Kürze wegen, AG = x, so hat man , also
oder nach 2., 3. und 4. T : t = b : B, und nach 1. T : t = B: b, also
No. 18. S. 73. Ist wie vorhin PO = b, AO = a (Fig. 26.), so wird als Subtangente , mithin MA = AO = a. Ferner ist SP = r = a + = AM + AS = MS, endlich da MSP gleichschenklig und SN (Fig. 26.) perpendikular auf MP, so ist MN = NP. No. 19. S. 76. Wegen der Proportionalität zwischen den Zeiten und den in ihnen beschriebenen Flächenräumen, möge die Fläche OT · SP in der Zeiteinheit beschrieben sein, die ganze Fläche E der Ellipse in T solchen Einheiten beschrieben werden; alsdann ist 1 : T = QT · SP : E also E = T · QT · SP = T.
No. 20. S. 77. Ist dieser grösste oder kleinste Abstand = c, so ist die Geschwindigkeit im Kegelschnitt proportional, im betreffenden Kreise ist der Parameter = 2c, mithin die Geschwindigkeit in demselben proportional; es verhält sich daher die erstere Geschwindigkeit zur letzteren, wie .
No. 21. S. 77. Die Abstände Sc und SC sind respective a und A, die Perpendikel Sd und SD b und B, die Parameter l und L hier und , die Geschwindigkeiten v und V; demnach und auch .No. 22. S. 78. Ist der Parameter = p, die Geschwindigkeit im Kegelschnitt = V, die im ersten Kreise = k, die im zweiten = K, der Abstand in diesem und im Kegelschnitt = r, das Perpendikel auf die Tangente = T; so hat man, nach Zusatz 8. V : k = ½p : T nach §. 18., Zusatz 6. , mithin .
No. 23. S. 83. Setzen wir die zu B gehörende Abscisse AM = x, die Ordinate BM = y, den Radius vector BS = r; so wird bekanntlich v² = (1 – e²)(2ax – x²) wo e die Excentricität der Ellipse ausdrückt, ferner weil AS = a(1 – e)r² = y² + (AS – x)² = (1 – e²) (2ax – x²) + (a(1 – e) – x)² und hieraus nach gehöriger Reductionund eben so, wenn AN = x1, CN = y1, SC = r1 gesetzt wird.
Da nun, wenn wir AG durch d bezeichnen, BK = d + x, LC = d + x1 nach Prop. 2. d + x : r = 2a : 2ae = 1 : e, so folgt
und nach derselben zweiten Proportion d + x1: r1 = 1 : e also
Vergleicht man 3. mit 1. und 4. mit 2., so gehören die Gleichungen 3. und 4. einer Ellipse an, wenn
Nach Prop. 4. des Textes ist aber 2ae : 2a = a(1 – e) : d also in der That de = e(1 – e) wie in 5.
No. 24. S. 84. Soll man K und k so bestimmen, dass VK : KS = Vk : kS = a : e werde, so ziehe man aus V unter beliebigem Winkel mit VS die Linie VM, mache auf dieser VL = a, LM = e = LN, ziehe MS und LK ∥ MS; alsdann ist VK : KS = VL : LM = a : e. Ferner ziehe man NS und Lk ∥ NS; alsdann ist Vk : kS = VL : LN = a : e; also auch VK : KS = Vk : kS.No. 25. S. 85. Man mache AB = SV (Fig. 36), AC = SP, AD = ab, ziehe BD und CE ∥ BD; alsdann ist AE = r.
No. 26. S. 86. Da MN = BZ – AZ, (Fig. 37.) so halbire man AB in U, trage rechts und links von U die gegebene Länge ½MN auf; alsdann ist MA gegeben. Macht man nun BV = MN, BW = MA, zieht man AW und XV ∥ AW; so hat man BX : BW = BV : AB, d. h. BX : MA = MN : AB also BX = PM (im Text).
Setzt man die grosse Axe MN = 2a (Fig. 37.), die Excentricität AB = 2ae; so ist MA = ½(AB – MN) = ae – a; also nach Prop. 1. .
Ist ferner die Abscisse des Punktes Z, in Bezug auf MA als Axe und M als Anfangspunkt, = x, der Radiusvector AZ = r; so wird und da r = ex + ae – a (§. 41., Bemerkung) , . Da nun ferner
No. 27. S. 89. Ist in einer Ellipse ein Halbmesser CB = a, sein ihm conjugirter Halbmesser CD = b, die Abscisse CL eines beliebigen Punktes H, in Bezug auf den ersten als Abscissenaxe = x, die zugehörige Ordinate HL = y, alsdann ist bekanntlich

Nun verlege man den Anfangspunkt der Coordinaten nach F, so dass CF = α sei; alsdann wird, wenn die Richtung der Coordinaten unverändert bleibt, die Abscisse FJ = CL = x, die Ordinate HJ = y1 = y — α, und daher nach 1. die Gleichung in Bezug auf die neuen Coordinaten
Aus 1. und 2. folgt
oder
Aus 3. folgt aber für y1 = 0
und hieraus . Substituirt man diesen Werth von α2 in Gl. 3., so ergiebt sich
Da nun y1 = HJ, γ + X = EJ, y1 + 2α = JK, γ — x = JG, so wird .

No. 28 S. 92. Ist ABDC das gegebene Viereck, und A + D = 180°, B + C = 180°, PQ AC, ST AB; so hat man in diesem Falle PQ · PR = PS · PT. Sind nun Pg, Pr, Ps, Pt respective perpendikulär auf AB, CD, AC, BD; so wird S = A = Q; sin R = sin SCD = sin B = sin T, mithin
und entweder
oder

No. 29. S. 101. Um die Linie dg zu construiren, verbinde man G mit O, ziehe aus d die Linie dg' DG, ziehe unter dem gegeben Winkel mit BL hier dg' die Linie dg und mache dg = dg', alsdann ist offenbar g'd : GD = Od : OD oder gd : Od = GD : OD.
No. 30. S. 106. Es ist nämlich, wenn man AC = a, CD = b, AL = x, JL = y setzt (Fig. 58). , und . Ferner EL = Subtg. = . , und oder CA : CL = EC : CA.
No. 31. S. 115. Aus den Proportionen
folgen die später in Anwendung kommenden, und zwar aus 1. BK : AK = HJ : GJ und AB : AK = GH : HJ. Aus 3. folgt Mi : iL = GJ : HJ oder Mi : iL = AK : BK.
No. 32. S. 120. Die der Zeit proportionale Fläche ASP ist nach § 68 = 4/3 GH · AS. Die ebenfalls der verwendeten Zeit proportionale Fläche ASp = ⅔AS · Sp = ⅔AS · 2AS = 4/3 AS · AS; mithin verhalten sich die erforderlichen Zeiten wie ASP : ASp = GH : AS.

No. 33. S. 120. Für einen dem Scheitel verschwindend nahe liegenden Punkt π drückt Aπ die Geschwindigkeit des Punktes A und Gh die Geschwindigkeit des Punktes G aus, wenn h der Mittelpunkt des durch π gehenden Kreises ist. Die Fläche ASπ ist nun nach §. 68., Gl. 5. = 4/3 · Gh · AS, aber sie ist auch, da Aπ verschwindend klein ist = mithin oder Gh : Aπ = 3 : 8.
No. 34. S. 124. Fig. 70. Setzt man OA = a, OS = ae und QOA = E, so wird aus OG : OA = OA : OS, OG = .
Ferner wird GF = OG · E = E sin AQ = a sin E, und daher der Sector AQS proportional e ( E — a sin E) = a (E — e sin E), ein Ausdruck, welcher dem in der theoria motus von Gauss befindlichen entspricht.
No. 35. S. 124. Fig. 71. Setzt man B = · 57°.29578 = e", wo e = sin φ und e" = e · 57°,29578, N = M, L = ,
No. 36. S. 125. In der Theorie motus befindet sich die Gleichung .
Setzt man daher hier ACQ = E, AC = a, SC = ae, so wird AQ = aE, das Perpendikel von S auf CQ = SC sin ACQ = ae sin E, und so hier APS = a (E — e sin E), d. h. APS proportional E — e sin E.
No. 37. S. 125. Setzt man der Kürze wegen CK = x, PK = z, CJ = ½e = ½, wo 2a und 2b die beiden Axen der Hyperbel bezeichnen, so ist AJKP = ½ ab log hyp. .
Ferner ist Δ CJA 1/8 e² sin AJC, Δ CKP = ½ xy sin CKP, = ½ · ¼ e² sin AJC, mithin Δ CJA = CKP, und indem man jedes dieser Dreiecke von CAPKC subtrahirt: AJKP = Δ APC.
No. 38. S. 129. Fig. 77. TC als Subtangente ist , wobei BO = AO = a, b die halbe kleine Axe, CP = y, OC = x und die Gleichung der Ellipse ist. Demnach wird TO = TC + CO = — x = und CO : BO = BO : TO wie Gl. 4 im Texte.
No. 39. S. 131. Fig. 80. Es ist Cd = y, Sc = x, SK = p, y² = 2px also .
No. 40. S. 144. Fig. 90. Durch den Unterschied der zwei ersten Kräfte wird der Weg mn, durch die zweite Kraft gleichzeitig der geradlinige Weg rϱ zurückgelegt. Das gesuchte Verhältniss ist daher mn : rϱ. Für die entstehenden Grössen ist aber und , mithin wird das gesuchte Verhältniss mk · ms : kr².
Im Lehrsatz, Gl. 1. und Zusatz 1., Gl. 5. war VCP : VCp = kr : mr = F : G mithin nun mr + kr : kr = G + F : F und mr — kr : kr = G — F : F d. h. (mr + kr) (mr — kr) : kr² = G² — F² : F² oder ms · mk : kr² = G² — F² : F². No. 41. S. 147. Es muss identisch R · G² — R · F² + T · F² — F²X = T³ — 3T² · X + 3T · X² — X³, also R · G² — R · F² + T · F² = T³ und F² = 3T² — 3TX + X². so wie für X verschwindend klein, wo der halbe Parameter R = T wird, d. h. G² : F² = 1 : 3 sein.
No. 42. S. 152. Nach Hansen, Schuhmachers Jahrbuch für 1837 Pag. 121. macht der Mond einen tropischen Umlauf in 27,321882 Tagen, und es bewegt sich seine Apsidenlinie in Einem Tage rechtläufig um 6' 41,0", mithin während eines tropischen Monates 3° 2' 56".
No. 43. S. 157. Dass VP Tangente an der Curve im Punkt P sei, (Fig. 93.) wird analytisch sehr leicht bewiesen. Man kann sieh aber auch wie im Text vorstellen, dass das Element der Curve bei P beschrieben wird, indem die Linie BP sich um B drehet; alsdann ist BP der Radius des osculirenden Kreises und die darauf senkrechte Linie VP Tangente an der Curve.
No. 44. S. 157. Da BV als Durchmesser constant, also sein Increment = ist, so wird das Increment von BV — VP identisch mit dem Decremente von VP.
No. 45. S. 157. Die Cycloïde ausserhalb und innerhalb der Kugel wird jetzt bezüglich Epicycloïde und Hypocycloïde genannt.
No. 46. S. 161. Setzt man den Bogen JH = s, LH = x (Fig. 95.) und nimmt man an, dass JH und KH um gleiche Incremente ds wachsen, so erhält man aus x = r — r cos s, wo der Radius durch r bezeichnet ist, und durch Differentiation
Ferner setze man den Quadranten HK = X, alsdann wird nach 1.
und so nach 1. und 2. dx : dX = r sin s : r = JL : GK. Da nun GK = GH = SR, GL = TR, und JL = .
No. 47. S. 161. Vorausgesetzt, dass HY und HZ als sehr klein angesehen werden dürfen, kann man den letzteren statt seiner Sehne setzen, und es ist HZ² = HY · MH = 2GH · HY, also HZ = oder proportional .

No. 48. S. 178. Die in diesem Zusatze ausgesprochenen Behauptungen in Betreff der Beschleunigung und Verzögerung der Bewegung des Körpers P durch die Kraft NM werden durch die nebenstehende Figur erläutert. Die Tangenten deuten die Richtung der Bewegung im Sinne des Pfeils an, die Kraft NM ist aber so in Seitenkräfte zerlegt, dass die eine der Richtung nach mit der Tangente zusammenfällt. Rechts von C und D wirkt NM im entgegengesetzten Sinne, weil hier QP > QS ist.
No. 49. S. 179. Ist C die Centripetalkraft, R der Radius, T die Umlaufszeit, a eine Constante, so hat man C = a · , also T = . Es nimmt daher T in demselben Verhältniss ab und zu, in welchem zu- und abnimmt.
No. 50. S. 183. Ist Q sehr entfernt von S, so werden die Linien LM und QM in demselben Verhältniss wachsen, wie PS : QS grösser

wird. In diesem Falle wird die Kraft QN sehr klein, und man kann NM = QM — QN statt QM setzen.
Nach der ursprünglichen Voraussetzung sind ferner diese Kräfte proportional . Wenn daher QK und PS constant sind, wird dieses Verhältniss gleich .
No. 51. S. 183. Ist d der constante wirkliche Durchmesser des Körpers Q, ϱ der von S aus gesehene scheinbare Durchmesser desselben; so hat man ϱ = und daher ϱ³ proportional .
No. 52. S. 193. (Fig. 107.) Es ist DF = DS — FS und df = ds — fs, also DF : df = DS — FS : ds — fs. Werden nun die Winkel DPE = FSE und dpe = fse verschwindend klein, so geht FS in ES und fs in es über, und es wird die Proportion
No. 53. S. 193. Die bei der Umdrehung durch den Bogen JH beschriebene Zone ist = 2SA · π · p, wo p den Abstand des Punktes Q von dem Fusspunkte des aus H auf AB gefällten Perpendikels bezeichnet. Denkt man sich dieses Perpendikel gezogen, fällt man auf dasselbe aus J das Perpendikel JM = p und zieht man JS; so ist Δ JSQ ∼ HJM, also SJ : JQ = HJ : p SJ · p = SA · p = JQ · JH und endlich JQ · JH proportional 2SA · π · p. No. 54. S. 195. Die Anziehung der einen Kugel sei = A, der Abstand des Körpers von ihrem Mittelpunkte = Δ, ihr Durchmesser = D. Dieselben Grössen in Bezug auf die zweite Kugel seien a, δ, d. und dabei
wo α eine Constante ist. Nach §. 114. ist
und indem man Δ so in Δ' vermindert, dass
so wird, wenn A' die nun entsprechende Anziehung bezeichnet,
also nach 2. und 4.
No. 55. S. 201. (Fig. 112.) Der Flächeninhalt dieser Zone ist bekanntlich = 2 · PE · π · Dd, also wenn PE constant ist, der Linie Dd proportional.
No. 56. S. 202. Um die Summe aller PD zu bilden, haben wir eine arithmetische Progression zu betrachten, deren erstes Glied = PD, letztes = PF und Differenz = Dd ist. Mithin wird die Summe aller PD = und das Produkt dieser Summe in Dd = ½(PF + PD)(Dd + PF - PD) und wenn wir Dd gegen PF — PD = DF vernachlässigen: = ½(PF² — PD²). Kürzer erhalten wir, indem wir PD = x und Dd = dx setzen xdx = ½(PF² — PD²).

No. 57. S. 205. Im Punkte A wird ALI = AL, im Puncto D wird DLII = DL, im Puncte B wird BLIII = BL und die beschriebene Fläche
Dasselbe ergiebt sich auch kurz folgendermassen, indem man die unbestimmte Ordinate LII D = y und nach der Voraussetzung = der Abscisse LD = x setz. Hiernach wird die beschriebene Fläche
No. 59. S. 206. Dies ergiebt sich unmittelbar wie im ersten Beispiel.
No. 60. S. 206. Setzt man LD = x, so wird die zu findende Fläche bestimmt durch .
No. 61. S. 206. Setzt man nämlich wieder LD = x, so erhält man nach der Reihe: ; ; .
No. 62. S. 207. Denkt man sich von L eine Tangente LT an den Kreis gezogen (Fig. 116.), so wird LA · LB = LT² = LS² — ST² = (LJ + JS)² — AS² = LJ² + 2LJ · JS + JS² — AS² = LJ² + PJ · JS + JS² — AS² = LJ² + JH² + JS² — AS² = LJ² + SH² — AS² mithin LA · LB = LJ² oder
Hieraus folgt LA : LJ = oder
und ebenso LB : LJ = , oder
Bringt man nun die drei Glieder im vorliegenden Beispiele unter gleiche Benennung, so erhält man zunächst den Ausdruck:
oder, weil LA = LS — AS, LB = LS + AS und LB + LA = 2LS, jener Ausdruck .
No. 63. S. 208. (Fig. 116.) Die beiden einzelnen Verhältniss sind hier und, das zusammengesetzte also
No. 64. S. 208. Wir haben in diesem Falle die einzelnen Verhältnisse und , als das zusammengesetzte = PS : JS = PS² : AS².
No. 65. S. 208. Aus und folgt durch Zusammensetzung .
No. 66. S. 208. Es ist Δ SPE ∼ SEJ, weil JS : SH = SH : PS d. h. JS : SE = SE : PS und JSE = PSE.
No. 67. S. 208. Es ist nämlich JE : PE = JS : SA = SA : PS = JS½ : PS½ mithin JEn : PEn = .
No. 68. S. 209. (Fig. 117.) Ist r der Radius der Engel, x die Höhe des Segments, so hat man den Flächeninhalt der Calotte = 2rπ · x, und daher die oben bezeichnete physische Fläche von der Dicke O = 2rxπ · O, mithin proportional rxO.
No. 69. S. 215. Setzt man PF = x, FK = y, so wird (Fig. 120.) .
No. 70. S. 215. Hier wird
No. 71. S. 215. Es ist nämlich PH = PD = , wo AP constant. Wenn daher AD = ∞ ist, so wird auch PH = ∞, und so für n > 1, .
No. 72. S. 216. (Fig. 121., I.) Setzt man PT = x, so wird 1 · dx = 1(PB - PA) = 1 · AB.
No. 73. S. 216. (Fig. 121., II.) Setzt man AD = RT = EB = r, so wird und
= (PE + C) — (PD + C) = PE — PD.
No. 74. S. 217. (Fig. 122.) Setzt man der Kürze wegen AP = α. AS = SB = b, PE = x, PD = ER = z, so ist nach §. 136., Zusatz 1. die Anziehung des Punktes P durch das Sphäroïd proportional
Man setze ferner ED = y, SC = a; alsdann wird
und hieraus
oder
Aus 3. folgt für x = α, bx = bα, und für x = α + 2b, bx = b (α + 2b). Da nun allgemein
ferner
oder aus dieser
so wird
Es ist aber AKRMB = AKMB + KMRK = 2b(α + b) + KMRK; mithin aus 6.
Weil aber α² + 2αb + a² = (α + b)² + a² — b², wird die Anziehung des Sphäroïds proportional
Ist hingegen eine Kugel über AB beschrieben, so wird bei der vorhergehenden Bezeichnung
für x = α, z = α, x = α + 2b, z = α + 2b und da allgemein
Hiernach verhält sich endlich die Anziehung des Sphäroïds zu der von Seiten der Kugel auf P ausgeübten Anziehung, wie
No. 75. S. 219. Setzt man CH = x, HM = y, so wird y = und daher die Fläche GLOK = also weil = 0, GLOK = .

No. 76. S. 221. Es sei x² = py, also y = ; alsdann wird und = Constans, und es drückt die Kraft aus, welche den Körper längs der Linie y anzieht.

No. 77. S. 221. Die Gleichung der Hyperbel in Beziehung auf die Asymptoten ist y = und hieraus , also nach der Bezeichnung im Texte die Kraft proportional . Derselbe Werth ergiebt sich, wenn man die Werthe m = — 1 und n = 1 in substituirt. Hingegen würde aus der Substitution derselben Werthe von m und n in der Werth B³ hervorgehen. Hiernach müsste, wenn ich nicht irre, der Schluss der Anmerkung im Texte geändert werden.
No. 78. S. 222. Vergl. §. 140.
No. 79. S. 222. Ist HC VW, wo VW die Hauptaxe der Parabel ist, so haben wir nach §. 31., Bemerkung. . Hier ist p der Parameter der Hauptaxe und α der Winkel, welchen die Tangente HM mit der Hauptaxe bildet. Da nun MJ = und x', MH = und y'; constant = P; so ist auch HM² = P · MJ. Zieht man eben so in J eine Tangente JL, nimmt MJZ als Durchmesser an und zieht man HZ JL; so ist MZ die Subtangente der Tangente MH in Bezug auf diesen Durchmesser als Abscissenaxe, und nach derselben Weise wie bei rechtwinkligen Coordinaten und der Hauptaxe als Abscissenlinie wird hier diese Subtangente MZ = 2 · JZ also MJ = JZ und somit ML = LH.
No. 80. S. 225.
| Genauer nach | Delambre | 493s,198 |
| „ | Struve | 497,827. |
No. 81. S. 227. Ist nämlich TR perpendikulär auf die Curve CDE so stellt PDR = TDA den Eintritts- RDS hingegen den Austrittswinkel dar. Wenn nun DP = DS, ferner PQ und SR auf DR senkrecht

sind, so ist der Eintrittssinus und der Austrittssinus. Da aber DE auf DR und EF auf DP senkrecht ist, so wird Δ DEF ∼ DPQ.
Ferner wird, da DE auf DR und EG auf DS senkrecht ist, auch Δ DEG ∼ DSR. Da nun der Eintrittssinus = und der Austrittssinus = ; so hat man DF : DG = Eintrittssinus : Austrittssinus.
No. 82. S. 231. Ist die ganze Zeit t = nτ gesetzt, wo n beliebig gross, so bilde man folgendes Tableau:
| Zeittbeile: | τ, | 2τ, | 3τ, | 4τ, | etc. . . | nτ |
| Geschwindigkeiten: | v, | vI, | vII, | vIII, | etc. | |
| Decremente der Geschwindigkeit: | av, | avI, | arII, | avIII, | etc. |
Alsdann ist
v — av = vI, vI — avI = vII, vII — avII = vIII, vIII — avIII = vIV = etc.,
also auch
v : v — vI = vI : vI — vII = vII : vII - vIII = vIII : vIII — vIV = etc. =
und nach §. 2. v : vI = vI : vII = vII : vIII = vIII : vIV = etc.
No. 83. S. 231. Aus dem vorhergehenden Tableau erhält man z. B.
eben so vIV : vVIII = ; mithin vIV = a4v, vVIII = a4 · vIV = a8 · v.
No. 84. S. 231. (Fig. 133.) Setzt man CD = x und DG = y, so ist die Gleichung der Hyperbel
Die hyperbolische Fläche wird daher
Eine zweite hyperbolische Fläche sei
Setzt man nun voraus, dass AI — A = Constans sei, so wird offenbar log. (xIa) — log. (xa) = log. = Constans oder auch
No. 85. S. 233. (Fig. 135.) Nach den Lehren der Kegelschnitte ist für eine Hyperbel CK · Kq = CA · AB = Constans, also CK : CA = AB : Kq, CA : CA — CK = Kq : Kq — AB, d. h. CA : AK = Kq : qk und hieraus CA : ½AH = Kq : ½qk.
No. 86. S. 233. Es ist nämlich
No. 87. S. 234. Wenn
ist, so wird auch
d. h.
wie aus der Bemerkung 84. hervorgeht. No. 88. S. 234. Aus ABqK : Bkq = ½AK, qKlr : gktr = AC : ½KL, rLMs : rlms = AC : ½LM, sMNt : smnt = AC : ½MN etc. etc. folgt für gleiche Intervalle, wo ABqK = qKLr = rLMs = sMNt = etc.
Bkq : gklr : rlms : smnt : etc. = AK : KL : LM : MN : etc. Das zweite fortlaufende Verhältniss ist mit dem in Bemerkung 84. identisch.
No. 89. S. 234, Z. B. Bms = ABsm — ABmM.
No. 90. S. 234. Ist R der ganze Widerstand im Anfange der Bewegung, welcher der Geschwindigkeit DP proportional ist, so wird der, der nach oben gerichteten Bewegung entsprechende und CP proportionale, Widerstand R(a) und man hat, wenn G die Kraft der Schwere bezeichnet,
also
No. 91. S. 236. Die Proportion QB : CK = DA : AC ergiebt sich, wie in §. 3. aus AC · AB = DC · DG oder AC : DC = DG : AB.

No. 92. S. 236. Drückt AB diese Geschwindigkeit, BC die ihr entsprechende Fallgeschwindigkeit aus, so ist der Parameter = .
No. 93. S. 237. Man setze den Parameter = p, die Kraft der Schwere constant = g, den Widerstand = r, die Geschwindigkeit = v; alsdann ist, wenn a, b, c constante Grössen bezeichnen, 2 · DP : p = g : r (Gl. 11.), p = av², r = bv, 2 · DP = = cv also der Geschwindigkeit proportional.
No. 94. S. 210. Aus der Gleichung der Hyperbel yx = c folgt, wenn die auf einander folgenden Werthe von x x, ax, a²x, a³x etc. sind, dass die entsprechenden Werthe von y werden:
Die erstern Werthe stehen daher in dem fortlaufenden Verhältniss 1 : a : a² : a³ : etc., die letzteren in dem umgekehrten:
1 : : etc. Ferner hat man (Fig. 139.)
also
No. 96. S. 241. Dies folgt aus §. 7.
No. 97. S. 242. Bezeichnet man die anfängliche Bewegung durch M, die Zeit durch T, den während der letzteren verlorenen Theil der Bewegung durch μ, die Zeittheilchen durch τ', τ", τ'" etc., die ihnen entsprechenden Verluste der Bewegung durch μ', μ", μ"' etc., den Widerstand durch R, und sind a, b, c, d, f etc. constante Grössen, so hat man μ = aRT, und damit μ = bM sei, muss RT = cM sein, mithin T = c · . Demnach wenn τ' = c · ; μ' = aRτ' = f · M und auch M — μ = (1 — b) M = f · M, proportional M.
Sind ferner V und v die Geschwindigkeiten beider Körper, T und t ihre Zeiten, S und s ihre Wege, M und m ihre Bewegungen; so hat man S : s = V · T : vt und da V : v = M : m auch S : s = MT : mt.
No. 98. S. 242. Zur vorhergehenden Bezeichnung komme C als Masse und D als Durchmesser, alsdann ist M = a · VC = bVD³, R = cD² · V², T = d · = f · , S = gV · T = hD.
No. 99. S. 242. Bei der vorhergehenden Bezeichnung ist hier R = aD3/2 ·V², T = b · , S = cVT = cV · b . = dV · = h · D3/2.
No. 100. S. 243. Das im Original gebrauchte Wort Genita glaube ich am passendsten durch das Wort Function ausdrücken zu können. Das Wort Momentum habe ich zunächst in deutscher Form beibehalten, da aber aus dem Lehnsatz hervorgeht, dass momentum genitae, oder nach meiner Ausdrucksweise, das Moment einer Function mit dem Differential der letzteren identisch ist; da ich mich ferner in meinen bisherigen Bemerkungen der allgemein gebräuchlichen Bezeichnung des Differentials bereits öfters bedien habe; so werde ich mir später auch in der Regel erlauben, im Texte statt der gegenwärtig weniger gebräuchlichen, oder auch wohl in einer anderen Bedeutung verstandenen Benennung Moment die gebräuchliche Differential zu setzen.
No. 101. S. 244. Der Coefficient von A ist hier , das Moment = a, der Cofficient von B ist hier = A, das Moment = b.
No. 102. S. 246. Es sei also A : B = B : C = C : D = D : E = E : F, und C constant, wie auch = M und D = CM, alsdann haben wir A = , B = , E= CM², F= CM³. Wir erhalten hieraus, wenn m das Moment (Differential) von M, a, b, d, e, f die Momente A, B, D, E, F bezeichnen, nach §. 10. Lehrsatz:
also a : b : d : e : f = — 2A : — B : D : 2E : 3F.
No. 103. S. 246. Aus A : B = C : D folgt, wenn B und C constant sind AD = BC = Constans, mithin Ad + aD = 0 und a : d = — A : D.
No. 104. S. 246. Aus A² ± B² = Constans folgt: 2aA ± 2bB = 0 und a : b = ± B : A.
No. 105. S. 246. In den beiden ersten Ausgaben dieses Werkes befand sich statt der Anmerkung, §. 11. die folgende: In Briefen, welche ich vor etwa 10 Jahren mit dem sehr gelehrten Mathematiker G. G. Leibnitz wechselte, zeigte ich demselben an, dass ich mich im Besitz einer Methode befände, nach welcher man Maxima und Minima bestimmen, Tangenten ziehen und ähnliche Aufgaben lösen könne, und zwar lasse sich dieselbe eben so gut auf irrationale, als auf rationale Grössen anwenden. Indem ich die Worte versetzte, welche meine Meinung (wenn eine Gleichung mit beliebig vielen veränderlichen Grössen gegeben ist, die Fluxionen zu finden, und umgekehrt) aussprachen, verbarg ich dieselbe. Der berühmte Mann antwortete mir darauf, er sei auf eine Methode derselben Art verfallen und theilte mir die seinige mit, welche von meiner kaum weiter abwich, als in der Form der Worte und Zeichen, den Formeln und der Idee der Erzeugung der Grössen. Die Grundlage beider Methoden ist im vorhergehenden Lehnsatze enthalten.
No. 106. S. 248. Aus AC : AP = (Fig. 142.) folgt nämlich, wie im §. 12., Lehrsatz AP = .
No. 107 S. 248. Eigentlich haben wir (Fig. 143.) ADv : pDq = Dt Dv : Dp Dq — Dt²: Dp · Dq. Da aber Dp und Dq nur wenig von einander verschieden sind, kann man ADv = · Dt² setzen.
No. 108. S. 260. In Bezug auf die Hyperbel ATZ ist AD = a, die halbe Axe = der sogenannten halben Zwergaxe AC, AX = x, TX = y, und es geht die allgemeine Gleichung der Hyperbel y² = (x² — a²) in diesem Falle über in y² = x² — a² oder x² — y² = a². No. 109. S. 250. Aus AP² = AC · AK, folgt, weil AC constant ist, 2AP · d · AP = AC · d · AK d. h. 2AP · PQ = AC · KL oder KL : PQ = 2AP : AC.
No. 110. S. 253. (Fig. 144.) Da HJ² = HM² + MJ² und HN² = HM² + (MJ — JN)² so wird ; , und weil JN sehr klein ist oder HJ — HN = .
No. 111. S. 253. Es ist beliebig MJ = Qξ + Rξ² + Sξ³ .... angenommen worden, hieraus folgt unmittelbar, weil NJ = MJ — MN und MN = Qξ ist, NJ = Rξ² + Sξ³ + etc.
Der Werth von MJ gilt allgemein für jeden Werth von ξ, mithin wird der entsprechende Werth in E für ξ = 2ξ 2Qξ + 4Rξ² + 8Sξ³ etc. in B für E = — ξ, — Qξ + Rξ² — Sξ³ und so DJ = CH — MJ = P — Qξ — Rξ² — Sξ³; EK = CH — 2Qξ — 4Rξ² — 8Sξ³ — etc. = P — 2Qξ — 4Rξ² — 8Sξ³ — etc. BG = P + Qξ — Rξ² + Sξ³ — etc.
No. 112. S. 254. Nach Gl. 12. und 10. ist (Fig. 144.) · GH =
nach Gl. 10. nach Gl. 8. 9. und 10.
mithin und nach 6. der Widerstand : Schwere .
No. 113. S. 254. Für CH als Durchmesser ist nämlich NJ = x die Abscisse, HN = y die Ordinate, und da allgemein die Gleichung der Parabel y² = px ist, .
No. 114 S. 254. Im Anfang dieses Paragraphen haben wir gesehen, dass die Zeit, in welcher der Körper den Bogen beschreibt, im halben Verhältniss der Höhe NJ steht, welche der Körper beim Falle von der Tangente HN in derselben Zeit beschreiben könnte. Nennt man jene kleine Zeit τ so ist , wo α constant. Die Geschwindigkeit, womit HJ beschrieben wird, ist daher
, d. h. proportional und ihr Quadrat proportional .
Bezeichnet man ξ durch Δx, so wird nach dem Taylor’schen Satze die obige Reihe allgemein:
also , , die Dichtigkeit des Mittels proportional .
No. 115. S. 255. Die hier im Text erwähnte Methode besteht offenbar in der Anwendung des binomischen Lehrsatzes. Es wird also

No. 116. S. 257. Setzt man FA = X, AQ = Y, FG = x, GJ = y, wo JG AQ; so hat man Y² = bX, y² = bx mithin Y² - y² = (Y + y) (Y - y) = b(X — x) oder PD · QD = b · JD. Hierbei ist der Parameter b constant.
No. 117. S. 258. Dieses Verhältniss ist nach der obigen Regel 13 §. 14. für den Punkt g, wo ξ = 0, 3S ·
No. 118. S. 258. Dieser Parameter ist nämlich nach §. 14.

No. 120. S. 261. Denkt man sich nämlich, in Bezug auf die Asymptoten XV und XT als coordinirte Axen, XP = x, PG = y als Coordinaten des Punktes G und die Tangente GT gezogen; so ist die Subtangente PT = x = PX. Demnach wird, wenn man VG XT zieht, erstere verlängert, bis VY = VG wird und hierauf XY zieht, im Viereck XYGT YG = XT und YG XT, also auch XY GT und XY = GT.
No. 121. S. 262. Bezeichnet man die Geschwindigkeit durch V, so ist V proportional ; also weil AH constant ist, AJ proportional
No. 122. S. 262. Die Dichtigkeit in A ist proportional , die in G proportional , die mittlere Dichtigkeit also proportional ; und so die Dichtigkeit in A zur mittleren wie = GT : ½(AH + GT).
No. 123. S. 262. Setzt man XY = y, AJ = x, so hat man die Gleichung der Hyperbel xyn = Constans; mithin wird , die Subtangente = + nx und HX = x + Subtangente = (n + 1) x = (n + 1) AJ.
No. 124. S. 264. (Fig. 151.) Wird AK = AE + EK = EK + KN + EN = e, AG = y, NK = AE = X, HN = Y gesetzt, so hat man AC : AE = NH : EN d. h. y : X = Y : x und xy = XY = Constans. Es liegt demnach H auf dem conjugirten Zweige derjenigen Hyperbel, auf welcher C sich befindet.
No. 125. S. 265. Setzt man JX = y und AJ = x, so ist die Gleichung der vorliegenden Parabel = Constans, während die Gleichung der vorhin erwähnten Hyperbel x · yn = Constans war. Offenbar hat man in der letzten Gleichung — n statt + n zu setzen, damit dieselbe in die vorhergehende Gleichung der Parabel übergehe. Durch eben diese Vertauschung erhält man den für den Parameter angegebenen Werth aus dem im Anfange dieses §. für die Hyperbel aufgestellten Werthe. No. 126. S. 268. (Fig. 154.) Man kann hier 2 AB · AP statt AP setzen, weil 2AB constant ist.
No. 127. S. 268. Es ist nämlich DPQ = , also proportional PQ, weil ½DB constant ist.
No. 128. S. 269. Die Gleichung der Hyperbel in Bezug auf ihren Mittelpunkt ist nämlich allgemein y² = (x² — a²). Im vorliegenden Falle ist aber y = TG, x = DG, b = BD = DF = a, GT² = DG² — DF².
No. 129. S. 273. (Fig. 160.) Offenbar ist V der mit dem Radius DA, aus D als Mittelpunkt beschriebene Bogen AG.
No. 130. S. 273. Eigentlich DET². Es ist aber DET = ½ET · DE = ½ V, also, insofern DE = DB und auch DA constant sind, DET² proportional V².

No. 131. S. 276. Es ist unmittelbar TQ : PD = TS : PE. Fällt nun Q mit P zusammen, so geht gleichzeitig T in P über und man kann PS statt TS setzen; es entsteht daher
No. 132. S. 276. (Fig. 161.) OP und OQ stehen nach der Voraussetzung auf der Spirallinie perpendikulär, und wenn die Punkte P und Q einander unendlich nahe liegen, werden beide sich auf dem Kreise befinden, welcher aus O mit OP = OQ als Radius geschlagen ist. Indem man in diesem Falle den unendlich kleinen Bogen PQ statt seiner Sehne setzt, ergibt sich nach bekannter Weise PD : PQ = PQ : 2PO.
No. 133. S. 277. Bezeichnet man die gleichen Winkel durch α, so wird, in so fern man die kleinen Bogen PQ und Qr als gerade Linien behandeln darf, PSQ = ½PS · PQ sin α, QSr = ½QS · Qr sin α und daher, weil PSQ = QSr, PQ : Qr = QS : PS.
No. 134. S. 277. (Fig. 161.) Es ist SV — SQ = VQ, also SP = SQ + VQ, wo VQ desto klein er wird, je näher P und Q einander kommen. Demnach wird SP — = SQ + VQ —
=Je kleiner nun VQ wird, desto mehr wird man die folgenden, höhere Potenzen von VQ enthaltenden, Glieder gegen das erste vernachlässigen können, und wir erhalten daher den Grenzwerth von SP — = ½VQ.
No. 135. S. 277. Diese Aehnlichkeit dürfte folgendermaassen zu erläutern sein. Da SV = SP, so ist SVP = SPV. Je näher nun Q an P rückt, desto kleiner wird der Winkel PSQ, und im Fall dieser verschwindend klein geworden ist, wird
Ferner ist im letztern Falle SPV = QPO = 90°, und zieht man hiervon ab SPQ = SPQ, so bleibt 2. QPV = OPS.
Es sind daher in den Dreiecken VPQ und OPS zwei Winkel einander gleich, mithin auch POS = PQV = SVQ.
No. 136. S. 277. Siehe erstes Buch, § 18, Zusatz 1.
No. 137. S. 278. Es wird alsdann ½VQ = ½PQ oder VQ = PQ. Der Körper nähert sich daher dem Centrum um eben so viel, als er sich fortbewegt. Die Bewegung erfolgt demnach längs PS.
No. 138. S. 278. Dies Verhältniss ist mit dem PQ : VQ identisch. (Gl. 8.)
No. 139. S. 279. Das Verhältniss PS : OS ist nach dem Lehrsatz = PV : VQ. In so fern nun PSV sehr klein ist, wird PV gleich dem aus S mit SP geschlagenen Bogen, und daher jenem Winkel proportional, während VQ die entsprechende Annäherung des Körpers zum Centrum S bezeichnet. Hieraus ergiebt sich, wenn der Winkel, welchen der Körper beschreiben muss, um von der einen Peripherie zur andern zu gelangen, durch α und der Abstand beider Peripherien durch a bezeichnet wird, α : PSV =a : VQ oder α = a · = a = a.
Das Verhältniss OP : OS ergiebt sich als der Zeit proportional unmittelbar aus Zusatz 5.
No. 140. S. 279. (Fig. 162.) Da nämlich AS : BS = BS : CS = CS : DS = etc. so wird auch
AS3/2 : BS3/2 = BS3/2 : CS3/2 = CS3/2 : DS3/2 = etc. Setzt man nun etwa = q, so wird AS3/2 + BS3/2 + CS3/2 + DS3/2 + .... in inf. =
und so
um so näher, je kleiner AB ist, indem alsdann die höhern Potenzen von AB vernachlässigt werden können.
No. 141. S. 280. Die Centripetalkraft ist proportional , ferner das Stück TQ proportional · t² (wie in §. 22., wo t die Zeit bezeichnet), also t umgekehrt proportional (§. 20.) = PQ · SP½n. Ferner der Widerstand in P proportional . Da nun PQ : QR = und PQ : Qr = QS : SP, so wird PQ : Rr = QS : Es ist aber PS = QS + VQ und = [QS½n + ½nQS½n-1 VQ + ....] QS1-½n = QS + ½nVQ + etc. Je kleiner nun VQ wird, desto eher wird man die folgenden höheren Potenzen gegen die erste vernachlässigen können. Es ergiebt sich also zuletzt PS — = QS + VQ — QS — ½nVQ = (1 — ½n)VQ.
Der Widerstand wird hiernach proportional
, indem man QS = PS setzt. Da nun auch der Widerstand proportional Dichtigkeit, so wird die Dichtigkeit proportional SPn Widerstand, also .
No. 142. S. 288. (Fig. 165.) AH drückt die Dichtigkeit, d. h. die Menge materieller Theile in A aus, deren jedes nach der Voraussetzung durch eine, proportionale, Kraft gegen S hin gezogen wird; daher muss AH · dasjenige ausdrücken, was man das specifische Gewicht nennt. Da ferner SA : SB = SB : SC = SC : SD = etc., so ist auch
d. h. AB : BC : CD: etc. = SB : SC : SD : etc., = SA : SB : SC : etc und so proportional proportional proportional u. s. w.
No. 143. S. 289. Ist SQ : SE = SE : SA, oder log SQ — log SE = log SE — log SA, so wird, weil EeqQ = n [log SQ — log SE] und EeaA = n [log SE — log SA], wo n eine beliebige Constante bezeichnet, Fläche EeqQ = EeaA.
No. 144. S. 291. (Fig. 167.) Eine harmonische Progression bilden die Glieder , etc.; soll also SA = , SD = , SF = sein, so wird oder 1. . Da nun ferner Aa : Dd = SD : SA und Dd : Ff = SP : SD, so wird 2. Aa — Dd = · Dd und Dd — Ff = · Dd, also nach 1. Aa — Dd = Dd — Ff. Aus thlx = xlnz folgt St : Sx = Sx : Sz nach Bem. 143.
No. 145. S. 291. Wenn n, nI, nII, nIII, nIV constante Zahlen bezeichnen, so hat man hier die Schwere = , etc. die Dichtigkeit = nIAH, nIBJ, etc. das specif. Gewicht = , , etc. die Drucktheile = , etc. = , etc. weil AB : BC etc, = SA : SB etc. Hiernach AH — BJ =
und tu : uw : wx etc. = etc. Da nun für die Rechtecke tp, uq, wr die Verhältnisse tp : uq: wr = th · tu : uw · iu : wx · rx = th · : ui · : rx · = (nach §., 30., Gl. 1.) stattfinden; so muss nach der Analogie mit §. 30., wie dort GL 2. hier die Gleichung richtig erwiesen werden. Da nun aber allgemein Aa · AS = Dd · DS = Ff · PS also Aa = Ff = ; so wird durch Substitution dieser Werthe von Aa und Ff die vorstehende Gleichung übergehen in welche hier vorausgesetzt wird.
No. 146. S. 292. Wir verfahren, wie in der vorhergehenden Bemerkung 145, vergrössern aber die Exponenten um 1; alsdann erhalten wir die Bedingung welche hier vorausgesetzt wird.
No. 147. S. 292. Wegen der constanten Schwere sind die Drucktheile nach der Reihe : AH · AB, BJ · BC, CK · CD, etc. oder, weil nach der Voraussetzung SA — SB = SB — SC = SC — SD = etc. = AB = BC = CD = etc so werden sie AH · AB, BJ · AB, CK · AB etc.
| Die Dichtigkeit | AH ist mithin proportional | [ | AH + | BJ + | CK + etc.] AB |
| BJ „ „ „ | [ | BJ + | CK + etc.] AB | ||
| CK „ „ „ | [ | CK + etc.] AC |
und wenn n eine Constante bezeichnet AH — BJ = n · AH · AB oder BJ = AH (1 — n · AB); BJ — CK = n · BJ · AB oder BJ = CK : (1 — n · AB) also BJ² = AH · CK oder AH : BJ = BJ : CK.
No. 148. S. 292. Hier wird die Schwere = nAS, etc. die Dichtigkeit = nI · AH, etc. das spec. Gewicht = nIIAH · AS, etc. der Drucktheil = nIIIAH · AS², etc, tu = AH — BS = nIII AH · AS²; uw = BJ — CK = nIIIBJ · BS²; tu : uw = AH · AS² : BJ · BS²; tp : uq = th · AH · AS² : ui · BJ · BS²; tp : uq = Aa · AS³ : Bb · BS³ (§. 30 Gl. 1.) Es muss mithin Aa · AS³ — Bb · BS³ = Bb · BS³ — Cc · CS³ d. h. AS³ — Bb · BS³ = Bb · BS³ — oder AS² — BS² = BS² — CS² sein, wie vorausgesetzt. No. 149. S. 292. Hier ist die Dichtigkeit = n · AH, die Schwere = das spec. Gewicht = die drückende Kraft = also nV · = nVIAH4 und so AH = ; hier sind n, nI, . . . . nVII constant.
No. 150. S. 292. Hier ist nV = nVIAH5 also AH = . Aehnlich beim folgenden Beispiel nV · = nVIAH², also AH = .
No. 151. S. 296. Bezeichnen M, P, T, L die Menge der Materie, das Gewicht, die Zeit und die Lange bei einem Pendel, m, p, t, l dieselben Grössen bei einem zweiten; so ist nach dem Lehrsatz, §. 34. für L = l, T² : t² = , für M = m und P = p, T² : t² = L : l daher überhaupt T² : t² = . Hieraus folgt M : m = , wie im Zusatz 5., ferner wird für T = t und M = m, L : l = P : p, wie in Zusatz 4.
No. 152. S. 302. Ist x die Geschwindigkeit, c eine Constante, so hat man nach der Voraussetzung R = ex², mithin dR = 2cxdz, und da x der in einem gegebenen Zeittheilchen beschriebene Weg, und dx, das Increment der Geschwindigkeit der antreibenden Kraft proportional ist, wenn wir das Zeittheilchen durch dt bezeichnen dR proportional x (V — R).
No. 153. S. 302. (Fig. 170.) Fällt RG auf QE, so wird OR = OQ und JGH = JEF und daher die Gleichung · JEF = JGH identisch. Fällt RG auf CT, so wird OR = OC; JGH = JLT, also · JEF = JLT, welche Gleichung nach 1. richtig ist.
No. 154. S. 303. Aus der Proportion dieses Zusatzes folgt
und das Differential des Widerstandes = PJGR — Y = 0.
No. 155. S. 304. (Fig. 171.) Setzt man MC = x, also MN = dx, so wird die Summe aller MN · CM
Setzt man nun eben so DK = y, BD = x, Dd = dx, so wird die Summe aller DK · Dd = ydx = d. h. gleich der Fläche BKVTa. Da nun jene Summen einander gleich, auch BKVTa = ½aB · Aa. No. 156. S. 305. Setzt man kurz die Geschwindigkeit DE im nicht widerstehenden Mittel = Y, die entsprechende Geschwindigkeit DK im widerstehenden Mittel = y; so hat man nahe bei y : Y = Ba : BA, oder y = Y und so BKVTa gleich einer Ellipse.
No. 157. S. 305. Da die Fläche der halben Ellipse = ½OV · BOπ, wo π die Ludolfsche Zahl, also genähert = ist; so wird
oder
No. 158. S. 305. Es wird nämlich 7/11Aa : CB = OV : CB, wo CB der Pendellänge gleich ist und die Schwerkraft ausdrückt, während OV den Widerstand in O bezeichnet.

No. 159. S. 305. Setzt man nämlich VO = x, VL = x', OB = y, KL = y'; so ist nach der Voraussetzung DK = c · DE² = c · DP · Da wo c eine Constante bezeichnet. Da nun DK = VO — VL = x — x'; DB = BO — KL = y — y' und da = aO + OD = y + y', so wird x — x' = c (y² — y'²) die Gleichung einer Parabel, da für x' = 0 und y' = 0 x = cy² wird.
No. 160. S. 307. Setzen wir die im Texte erhaltenen mittleren Differenzen der beschriebenen Bogen = a, = b, = c, = d, = e, = f, so erhalten wir deren Verhältnisse, welche die
Die auf einander folgenden Schwingungen seien A = , B = , C = 15, D = 30, E = 60, F = 120 und es wird offenbar (A : A)² = 1, (B : A)² = 4, (C : A)² = 16, (D : A)² = 64, (E : A)² = 256, (F : A)² = 1024. Während diese Zahlen nach einander im constanten Verhältniss 1 : 4 stehen, nähern sich die vorher aufgeführten Zahlen diesem Verhältniss, indem
No 161. S. 308. Betrachtet man den Widerstand der Kugel als aus drei Theilen bestehend, von denen der erste der Geschwindigkeit V selbst, der zweite ihrer 3/2ten Potenz, der dritte ihrer 2ten Potenz proportional ist;
| so ist der Coëfficient des | ersten | nach §. 40., Zusatz | = 7/11, |
| „ „ „ „ | dritten Theiles | „ „ | = ¾ |
und weil V3/2 = , der Coëfficient des zweiten Theiles = = 0,69085, oder näherungsweise = 7/10 Texte. No. 162. S. 309. Da die Radien dem Bogen proportional sind, haben wir 121 : 1195/29 = 126 : x, x = 124 + 2,8/29 = 1243/31 sehr nahe.

No. 163. S. 309. Für den Umwälzungswinkel PQN = z und den Radius des erzeugenden Kreises PQ = r, ist bei der Cycloïde DPS, DN = x = sinus versus z = 2r sin ½z², DP = 4r sin ½z, DS = 4r sin ½π = 4r = der Pendellänge; also
No. 164. S. 309. Wir nehmen an, dass der Verlust an Bewegung der Kugel ihrem zurückgelegten Wege proportional sei. Wir haben daher nach dem Vorhergehenden die Proportion 30,656 : 3,4375 = : x und hieraus x = . In der ersten Ausgabe stand
No. 165. S. 311. Wie aus dem Folgenden hervorgeht, kann Newton unter den 5 Schwingungen nur doppelte verstanden haben, welche aus zweimaligen Fallen und Steigen zusammengesetzt waren.
No. 166. S. 319. Ist die Geschwindigkeit = c, der Abstand der Theilchen = r, die Quantität der Materie = q, der Durchmesser = d, die Dichtigkeit = Δ und sind n, n', n", n'" constante Zahlen; so ist der Widerstand R = n . Da nun r = n' · d; q = n"Δd³, so wird R = n · = n"' · c² · d² ·Δ.
No. 167. S. 320. Bezeichnen d, e, f, g respective die Widerstände, welche die Körper D, E, F, G erleiden, so ist d : e = T : V; f : g = T : V, also d : f = e : g.
No. 168. S. 322. Drückt man die Intensität der Kraft, welche das Theilchen des Mittels längs FB ausübt, durch LB aus; so kann man diese in die Seitenkräfte LD und BD zerlegen. Die letztere wirkt längs der Tangente BD und wird die Kugel gar nicht bewegen, die erstere hingegen wirkt perpendikulär gegen die Kugel längs BC und sie verhält sich zur ursprünglichen, perpendikulär gegen den Cylinder wirkenden Kraft, wie LD : BL = BE : BC. Wenn man nun in der Figur des Textes Dm auf BL perpendikulär fällt, so kann man die eben gefundene Kraft DL in die beiden Seitenkräfte nD und mL zerlegen. Erstere wirkt längs Bβ Dm und wird, weil sie von B gegen β wirkt, durch eine ihr entsprechende, aus dem in β aufstossenden Theilchen hervorgehenden Kraft aufgehoben. Die andere Kraft mL allein wird das Bestreben haben, die Kugel längs FB zu bewegen und sie verhält sich zu DL, wie mL : DL = BE : BC; mithin wird mL : BL = BE² : BC². No. 169. S. 323. Fällt man in der Figur des Textes das Perpendikel Hk auf CA und setzt man Hk = bA = EC = y, Ck = x, also bH = Ak = AC — x; so wird BE² = BC² — CE² = AC² — y² und die Gleichung bH = gebt über in AC — x = , d. h. in y² = AC · x, die Gleichung der Parabel. Ferner ist der Cubikinhalt des Paraboloïds = = ½AC³ · π, dagegen der Inhalt des Cylinders = AC³ · π; also das Paraboloïd = ½ Cylinder.
No. 170. S. 323. Setzt man den Widerstand, welchen das Mittel gegen einen, über CEB zur Hohe OS construirten Cylinder ausüben würde, = p · CEB, wo p eine Constante ist; so hat man nach §. 45. den gegen den ganzen Kegel CBS ausgeübten Widerstand
den gegen den kleinen Kegel FGS ausgeübten
endlich den gegen die Fläche FG ausgeübten Widerstand
Hiernach wird der, gegen den abgekürzten Kegel ausgeübte Widerstand
Setzt man nun CO = b, OD = a, DS = x, so wird CEB : FG = (a + x)² : x², also
und ausserdem
Nach §. 4. ist daher der Widerstand
und da p und CEB beide constant, so muss x so bestimmt werden, dass nach gehöriger Reduction
ein Minimum werde. Wir erhalten demnach durch Differentiation
Aus F'(x) = 0 oder Z = 0 folgt
also
Ferner wird aus 8., weil Z = 0,
No. 171. S. 321 Stellt GO BR den Widerstand dar, welchen das Mittel gegen GH ausüben würde, so drückt, wenn man OK auf GR und KL auf OG perpendiculär zieht, OL den gegen GB ausgeübten Widerstand des Mittels aus. Da nun GR parallel der Tangente in N ist, so wird MN · LG den MN entsprechenden Widerstand darstellen und es ist Bedingung, dass derselbe ein Minimum werde, oder da MN gegeben ist, muss
werden. Nun ist
also
also
Die Linien OG und GB sind gegeben, daher muss, wenn LO ein Minimum sein soll, GR² ein Maximum, oder weil
BR ein Maximum werden. Bezeichnet nun a eine später zu bestimmende Constante, so muss MN · LO — a · BR ein Minimum werden. Hieraus ergiebt sich durch Differentiation, weil MN und a constant sind,
und aus 5.
Multiplicirt man nun die drei Gleichungen 6., 7. und 8. in einander, so erhält man
Denkt man sich nun N nach G verlegt, so wird nach dem Schluss der vorhergehenden Bemerkung GR² = GP² = GB² + BP² = 2 · GB²; MN = GB, BR = BP = BG, LO = ½GO, also nach 9. 2a · GB² = — GB² · GO oder a = — ½GO und es geht Gl. 9. mittelst dieses Werthes von a über in
Da aber nach 4. GO = , so wird aus 10. GR4 = 4MN · BR · GB² oder
No. 172. S. 325. (Fig. 174.) Drückt CB die Bewegung aus, welche in der Zeit AB durch den Widerstand verloren geht, so wird der ganze Weg, nach §. 7., Zusatz 1., durch CBEF ausgedrückt. Die dann stattfindende Bewegung wird durch EF bezeichnet, also ist FG verlorgen gegangen. Soll BC den Widerstand im Anfange der Zeit BE, BH den Widerstand am Ende derselben ausdrücken; so muss, weil der Widerstand dem Quadrate der Bewegung proportional ist, wenn BH = α · EF² ist, auch BC = α · BC² sein, wo α constant. Nun ist BH : EF = AB : AE = EF : BC, also BH = · EF² und auch BC = · BC². In ersteren Falle hat also der Widerstand den Theil CH verloren.
No. 173. S. 326. Nach Zusatz 6. ist AB = T, BE = t, BC = M, mithin EF = BC = M, GF = BC — EF = M. Ferner ist BGGE = BC · BE = Mt, BCFE = EF · dAE = also BCFE : BCGE = log . Dieser Logarithme ist ein hyperbolischer, daher muss der Briggsche Logarithme log durch die im Texte aufgeführte Zahl, d. h. das Reciproke des Modulus der Briggschen Logarithmen multiplicirt werden, um denselben in einen hyperbolischen zu verwandeln.
No. 174. S. 327. Bezeichnet t die Zeit, c und c' die Geschwindigkeiten, h und h' die Wege, g = 155/8 Fuss die bekannte constante Fallhöhe; so ist h = gt², c = = 2gt, also auch c = 2 und eben so c' = 2, mithin c : c' = oder h : h' = c² : c².
| Entspricht nun der Geschwindigkeit | c | der Querschnitt | s |
| „ „ | c' | „ „ | s', |
so ist bei gleicher Zeit t im ersten Falle die Wassermenge m = cst, im zweiten Falle m' = c's't und wenn m = m', cs = c's' oder c : c' = s' : s.

No. 175. S. 330. Bei einer Fallhöhe = h ist die Geschwindigkeit, nach der vorhergehenden Bemerkung, weil die Oeffnung sehr klein ist, c = 2. Diese hat man hier horizontal anzunehmen, und es wird in einer kleinen Zeit t ein Weg
beschrieben. Während derselben Zeit fällt aber der Wasserkörper, vermöge der Schwere, um eine Länge
Eliminirt man t aus 1. und 2., so wird
die Gleichung einer Parabel, deren Parameter = 4h ist. In vorliegendem Falle hat man h = 20", mithin den Parameter = 80" und für y =20",
No. 176. S. 332 (Fig. 176.) Aus JO² = JH · JG, oder JH : JO = JO : JG folgt JH : JO — JH = JO : JG — JO oder JH : HO = JO : OG; hierauf HO + OG : 2HO = JH + JO : 2JH und auch JH + JO : 2JH = JO + JG : 2JO = AB + EF : 2EF.
No. 177. S. 335. (Fig. 178.) Das neben dem Kreise vorüberfliessende Wasser habe die nach unten gerichtete Geschwindigkeit h', und dabei ist der Querschnitt des Raumes, wodurch es fliesst = (EF² — PQ²)π. Die nach oben gerichtete Geschwindigkeit des Kreises sei h, wobei sein Querschnitt = PQ² · π ist Bei gleicher Dauer beider Bewegungen haben wir daher (EF² — PQ²) πh' = PQ²πh, also h : h' = EF² — PQ² : PQ² und hieraus h : h + h' = EF² — PQ² : EF².

No. 178. S. 341. Es bezeichne d den Durchmesser der Kugel, s den Weg, welchen sie zurücklegt, während sie die Hälfte ihrer Bewegung verliert. Alsdann ist EF = ½BC, und weil
Da nun a. a. O. AB = T, BE = t war, AE = 2AB = 2T = T + t, oder t = T. Ist die anfängliche Bewegung BB = M, so hat man nach §. 47, Zusatz 7.
In diesem Falle wird AB · BB = BCGE = Mt, und da allgemein BCGE : AB · BC, wie der Weg, welchen die Kugel mit ihrer anfänglichen Bewegung BC in der Zeit t = BE zurückgelegt hätte, an dem Wege, welchen sie in der Zeit T zurücklegen würde, während welcher ihre ganze Bewegung durch den Widerstand des Mittels angehoben werden könnte; so sind beide Wege in diesem Falle einander gleich, also nach diesem Paragraphen = 8/3d. Demnach geht vorstehende Proportion über in s : 8/3d = 2,30258 .... 0,30103 : 1, woraus s = 1,84d, d. h. s < 2d folgt.
No. 179. S. 342. (Fig. 143.) Es bezeichne V die Geschwindigkeit, welche die Kugel bei ihrem Falle in zusammengedrückter Flüssigkeit während der Zeit P erlangt haben würde. Es sei nun
und man ziehe durch den Punkt T der Hyperbel AVZ, πτ AC, bis die erstere die Hyperbel in τ und die Asymptote DC in π schneidet. Da nun aus TX² = DX² — DA² (§. 13.) = πX² — AC² folgt
also
so wird
und auch
so wie
Da nun ferner πX CA, so ist πX : TX = AC : AP = H : V (Gl. 1.) und so (nach Gl. 6.)
Setzt man DX = x, τX = TX = y, DA = AC = a, so wird Δ ADC
Ferner folgt aus y² = x² — a², dy = und so
endlich
Hier bezeichnet in einen natürlichen Logarithmen, hingegen soll log einen Briggischen bezeichnen. Setzt man nämlich β = 0,4342944819 gleich dem Modulus der Briggischen Logarithmen, so folgt ans Gl. 8.
Ferner ist
und
Der während der Zeit P beschriebene Weg werde durch A, dagegen der von einem beliebigen Körper, in derselben Zeit P mit der Geschwindigkeit H beschriebene, Weg durch S bezeichnet. Alsdann ist in der Figur
also
Ferner wird, wenn man NK = y, CK = x, ¼AC² = α² setzt, yx = α² und
Nach §. 13. ist AC : AP : = AP : AK, also AC : AK = AC² : AP², und daher AC : CK = AC² : AC² — AP² = H² : H² — V² (Gl. 1.)
also wird
Nach §. 13., Zusatz 1. ist ABNK : ADT = A : S, mithin
oder
<centerA log N = S · .Da nun S und 2F die Wege sind, welche die mit der Geschwindigkeit H gleichförmig fortschreitenden Körper in den Zeiten P und G zurücklegen würden; so ist
und
Aus Gl. 14. und 15. folgt demnach A log N = [2L + log N — log 4] d. h. weil oben
Mittelst des Werthes von β = 0,4342944619 und log 4 = 0,6020599913 wird = 4,60517086, = 1,3862945611, also A, oder die in der Zeit P zurückgelegte Höhe
Ist A sehr gross, so dass AP in §. 13. der Linie AC sehr nahe gleich wird, so fällt nach Gl. 7. πτ² sehr gross im Vergleich mit AC² aus, d. h. es wird nach Gl. 8. N sehr gross und kaum grösser als 1. Hiernach wird ferner L = log sehr nahe = 0 und man kann daher in Gl. 17. das Glied 4,60517086 LF vernachlässigen.
No. 180 S. 343. Ein Körper verliert, wie wir oben in Abschnitt V. gesehen haben, wenn er in Wasser eingetaucht wird, so viel von seinem Gewicht, als ein Wasserkörper von gleicher Grösse wiegt. Hiernach wird das Gewicht einer beliebigen Wasserkugel dem Unterschiede des Gewichtes einer gleich grossen Kugel im leeren Raume und im Wasser gleich sein.
No. 181. S. 343. Ist dieser Durchmesser d, so wird d = 1" · = 0,84224 Zoll. No. 182. S. 344. Zur Erläuterang der im Texte aufgeführten einzelnen Rechnungen, diene Folgendes. Aus 2,24597 : 2F = 7913/38 : 15613/38 folgt 2F = 4,4256 Zoll. Für den Fall der 15613/38 Gran im leeren Raume wiegenden Kugel, ist das beim Falle der Körper vorkommende g = 193⅓ Zoll. Im Wasser wiegt die Kugel nur 77 Gran, und daher wird die 1 Secunde entsprechende Fallhöhe = · 193⅓ = 95,219 Zoll. Setzt man nun s = 95,219 = g¹ t² = g¹ 1 Sec., F = 2,2128 = g¹ · G², so wird G : 1 = oder G = 0,15244 Secunde. Ferner wird = H = 2g¹G, mithin H · G = 2g¹G² = 2F. Aus der Proportion 0,15244 : 4 = 2F : S, folgt der 4 Secunden entsprechende Weg S = 116,1245 Zoll. Hiervon muss nach §. 60, 1,3862944 F = 3,0676 Zoll subtrahirt werden. Endlich ergiebt sich aus dem im Texte gegebenen Durchmesser = 0",84224 oder Halbmesser = 0,42112 Zoll der grösste Kreis der Kugel = 0,55715 Quadratzoll, der horizontale Querschnitt des Kastens = 81, mithin die zwei einzelnen Verhältnisse und 81 : 80,44285 und hieraus das zusammengesetzte Verhältniss 1 : 0,9914. Der im Text aufgeführte Weg 113,0569 Zoll muss daher in diesem Verhältnisse vermindert oder mit multiplicirt werden und gebt so in 112,08 Zoll über.
| No. 183. S. 357. Diess lässt sich noch deutlicher aus einer graphischen Darstellung ersehen. Bezeichnen a, b, c, d, e, f u. s. w. einzelne Theilchen, geben die Pfeile die Richtung der Bewegung an, wobei a, c, e einerlei, b, d, f die entgegengesetzte Richtung haben; so findet im oberen Falle eine Verdichtung, im untern Falle eine Verdünnung der zunächst auf einander folgenden Theile statt. |
No. 184. S. 362. (Fig. 184., 185.) Im ersten Falle
Im zweiten Falle ist Gγ — Eε = (Gε + εγ) — (EG + Gε) = εγ — GE = Pn — Pl = ln oder εγ = GE + In.
No. 185. S. 362. Denkt man sich aus K eine Linie Kn LN und = LN, so wird Δ KHn ∼ JMO, weil die Seiten beider Dreiecke auf einander perpendikulär stehen, mithin Kn : KH = JM : JO oder LN : KH = JM : OP.
No. 186. S. 365. (Fig. 184.) Es ist nämlich HL = sin PH und KN = sin PK. Fällt nun K mit P zusammen, so wird KN = sin O = 0 und es kann HL = sin PH alsdann = PH oder = KH gesetzt werden, weil wegen der Kleinheit der Linie EG der Bogen KH = PH nothwendig sehr klein ist.
No. 187. S. 365. Setzt man die eine Kraft; = 2g, die andere = 2g', die entsprechenden Zeiten = t und t' und den von beiden beschriebenen gleichen Weg = s, so hat man s = gt² und s = g't'² also gt² = g't'² und t : t' = .
No. 188. S. 366. Wir haben nämlich die Proportion
No. 189. S. 367. Nach der im Texte aufgestellten Hypothese kann man die Wasser- und Lufttheilchen einander gleich und = 1 annehmen. Im Wasser liegen sie unmittelbar nebeneinander, nimmt man dagegen den Abstand ihrer Mittelpunkte von einander in der Luft = 9 oder = 10 an, so wird dasselbe Volumen Luft oder , d. h. oder der Menge fester Theilchen enthalten, welche sich im Wasserkörper befinden. Beide Verhältnisse schliessen das im Text angenommene ein.
No. 190. S. 369. (Fig. 186.) Setzt man nämlich SD = x, Dd = y; so wird, weil SQ = ∞ und nach der Construction y = anzunehmen ist, die Fläche DdQ = ydx = + . Es ist also DdQ umgekehrt proportional x oder SD.
No. 191. S. 371. Setzt man allgemein SD = x, Dd = y, C = Constans,
also DdQ umgekehrt proportional SD² und die Umlaufszeit direct proportional SD².
No. 192. S. 374. Im Fall Kugel, Flüssigkeit und Gefäss sich nach Zusatz 7. um eine gemeinschaftliche Axe drehten, sei
| die Winkelbewegung | die Umlaufszeit | der Radius | |
| für die Kugel | G | γ | S |
| für einen Punkt der Flüssigkeit | K | κ | k |
| für das Gefäss | E | ε | e; |
alsdann ist nach Zusatz 7.
also auch
ferner
also aus 4. und 5.
oder
Aus 3. folgt
nach 6. u. 7. ist daher
Nach 2 ist
also
Hier bezeichnet K – P die Winkelbewegung der Kugel bei ruhendem Gefässe, also K – P + P = K dieselbe in Bezug auf die entgegengesetzt bewegte Ebene. Es folgt aus 8. oder aus 2. für E = P, K : P = e² : k² und was von dem beliebigen Punkte der Flüssigkeit gilt, gilt auch von jedem andern.
No. 196. S. 377. Statt „Hypothese von Copernicus, müsste hier nach meiner unmassgeblichen Meinung zu lesen sein: „Keplers Gesetzen“.
No. 194. S. 378. Im Berliner astronomischen Jahrbuche für 1871 Pag. 166 folg, findet man beiläufig
| log r(♀) | log r'(♂) | |||||||||||
| für | die | Fische | oder | die | Länge | 330° | 9,8621 | 0,1404 | r | = 0,728 | r' | = 1,382 |
| „ | „ | Jungfrau | „ | „ | „ | 150 | 9,8566 | 0,2216 | =0,719 | =1,666 | ||
| mithin für | 330° | r' – r = 0,654 |
| 150 | r' – r = 0,947 |
also diese Abstände für die Zeichen der Jungfrau und der Fische nahe im Verhältniss 3 : 2.
No. 195. S. 378. A. a. O. Pag. 9 und Pag. 45 finden wir
| für | Länge | ☉ | = 330°, | Δ☉ = 60′ | |
| „ | „ | „ | = 150 | Δ☉ = 58 | |
| also umgekehrt | für | Länge | ♁ | = 150° | Δ♁ = 60′ |
| „ | „ | „ | = 330 | Δ♁ = 58. |
No. 196. S. 382. Nach den neuern Angaben von Hansen in Schumacher’s Jahrbuch für 1837, sind die
| Umlaufszeit der vier Trabanten | 1d 18h 28m, | 3d 13h 14m, | 7d 8h 43m, | 16d 16h 42m |
| deren gegenwärtiges Verhältniss | 1 | 2,007 | 4,044 | 9,432 |
| ihr doppeltes | 1 | 4,028 | 16,351 | 88,958 |
| die Abstände | 6,049 | 9,623 | 15,350 | 26,998 |
| ihr gegenwärtiges Verhältniss | 1 | 1,591 | 2,538 | 4,463 |
| „ dreifaches „ | 1 | 4,026 | 16,341 | 88,910 |
| Die zweite Angabe Cassini’s im Text giebt das doppelte Verhältniss der Zeiten | 1 | 4,028 | 16,353 | 88,983 |
| das dreifache Verhältniss der Abstände | 1 | 4,006 | 16,354 | 88,991 |
No. 197, S. 382. Hansen giebt a. a. O. die Zahlen:
| 163107, | 236482, | 390312, | 1377672, | 6853620 | |
| ihr einfaches Verhältniss | 1 | 1,450 | 2,393 | 8,446 | 42,02 |
| ihr doppeltes Verhältniss | 1 | 2,102 | 5,726 | 71,33 | 1765,6 |
| die Abstände der Trabanten nach Cassini | 1,95 | 2,6 | 3,5 | 8 | 24 |
| ihr einfaches Verhältniss | 1 | 1,2820 | 1,7950 | 4,1025 | 12,307 |
| ihr dreifaches Verhältniss | 1 | 2,107 | 5,783 | 69,05 | 1864,0 |
No. 199. S. 383. Hansen giebt a. a. O. für diesen Werth 17″,1 an.
No. 200. S. 384. Nach Hansen hat man, mit Einschluss der ♀ und des ![]()
No. 201. S. 385. Der Exponent 2 + ist von 2 um , von 3 um entfernt, also dem ersteren Werthe näher als dem zweiten im Verhältniss 4 : 239 =
No. 202. S. 386. Da der siderische Monat = 27d 7st. 43m ist, so wird 1m = der ganzen Umlaufszeit in einem Kreise, dessen Durchmesser = 120 Erdhalbmessern ist. Im Text ist der Umfang der Erde = 123249600 Fuss angenommen worden, woraus der Log seines Halbmesser = [7,2926056] folgt. Betrachtet man nun den kleinen, in 1 Minute durchlaufenen Bogen als mit seiner Sehne identisch, so erhält man den gesuchten Sinus versus = x aus der Proportion
wo log r = 7,2926056; also wird x = 15,009 Fuss.
Diesen Weg legt der Mond vermöge der Kraft zurück, welche ihn in seiner Bahn erhält; dieselbe ist der Unterschied der beiden, nach dem Mittelpunkt der Erde und nach dem Centrum der Sonne gerichteten, Kräfte; sie ist daher kleiner, als jene nach dem Centrum der Erde gerichtete und zwar im Verhältniss 17775 : 17875. Vergrössert man daher den für x gefundenen Werth in eben diesem Verhältniss, so erhält man 15,093 Fuss = 15 Fuss 1 Zoll 17/17 Linien Par. Mass.
No. 203. S. 387. Den Radius der Kreisbahn, welchen der Mond um die im Centrum der Bahn unbewegliche Erde beschreiben würde, ist nämlich kleiner, als der Abstand des Mondes vom Mittelpunkte der Erde, wenn ersterer sich um den gemeinschaftlichen Schwerpunkt beider Körper bewegte (§. 101. des ersten Buches). Aus diesem Grunde setzt Newton den Radius jener Bahn nur = 60 Halbmessern, obgleich das arithmetische Mittel der grössten und kleinsten Entfernung nicht kleiner als 60½ Halbmesser ist. Dass er in dieser Sache richtig geschlossen habe, hiervon überzeugte er sich dadurch, dass wenn man jenen Abstand von 60 Halbmessern in demjenigen Verhältnisse vergrösserte, in welchem bei unverändertem Gesetze der Schwere der Abstand des Mondes von der beweglichen Erde jenen Radius übertreffen muss, offenbar eine Länge von 60½ Erdhalbmessern herauskommen muss, wie die Astronomen für diese Entfernung gefunden haben.
Reduciren wir g(t) und g(i) auf den Punkt M, so erhalten wir für erstere und für letztere indem wir SM = Δ, MT = a und MJ = ax gesetzt haben. Wenn wenn wir daher nach 1. g(t) = g(i) setzen, erhalten wir
oder
und hieraus
Vernachlässigen wir a gegen Δ so folgt hieraus
oder genähert
No. 205. S. 393. Bei der folgendermassen ausgeführten Rechnung habe ich Resultate erhalten, welche von den im Texte angegebenen etwas abweichen.
Bezeichnet r den Abstand vom Centralkörper und t die Umlaufszeit, so ist nach der 4. Erscheinung und §. 10.
| d | |||||||||
| für | die Sonne | und | Venus | r = | 72333 | t | = 224,698 | ||
| den | Jupiter | „ | 4. | Trabanten | 520096 sin 8′ 16″ | „ | = 16,689 | ||
| „ | Saturn | „ | 6. | „ | 954006 sin 3′ 4″ | „ | = 15,944 | ||
| die Erde | „ | der Mond | 100000 sin 10′ 33″ | „ | = 27,322. | ||||
Nach §. 18. Zusatz 2. des ersten Buches wird das Gewicht allgemein ausgedrückt durch . Mithin ist das Gewicht der Venus gegen die Sonne im Abstande 72333 = ; das Gewicht des 4. Trabanten gegen den Jupiter im Abstande 520096 sin 8″ 16″ = , dasselbe im Abstande 72333 = oder = ; eben so das Gewicht des 6. Trabanten gegen den Saturn im Abstande 72333 = ; das Gewicht des Mondes gegen die Erde im Abstände 72333 = . In so fern wir das Gewicht der Venus gegen die Sonne, oder als Einheit annehmen, erhalten wir die Gewichte
| des | 4. | Trabanten | gegen | den | Jupiter | = · 224,698² |
| „ | 6. | „ | „ | „ | Saturn | = · 224,698² |
| „ | Mondes | „ | die | Erde | = · 224,698². | |
Nach der ausgeführten Rechnung haben sich statt der im Texte aufgeführten Werthe, die folgenden ergeben:
No. 206. S. 393. Die eben gefundenen Werthe der Gewichte gegen die verschiedenen Himmelskörper gelten für die gleiche Entfernung von ihren Mittelpunkten = 72333. Will man dieselben auf die im Texte angegebenen Abstände reduciren, so erhalten wir respective die Werthe
Sie verhalten sich also zu einander wie
oder wie 10000 : 943 : 517 : 435.
| Setzt man | statt | 3091 | wie | im | Original | 3021 |
| „ | 193594 | „ | „ | „ | 169282, |
so ergeben sich in der fortlaufenden Proportion respective die Werthe 529 : 496.
No. 207. S. 394. Die Parallaxe der Sonne ist nach Encke = 8,″5776; mithin muss das Gewicht oder die Masse der Erde mit multiplicirt werden. Das im Text gefundene wird in diesem Falle = ; hingegen der in der Bemerkung 205) gefundene Werth . Hansen hat a. a. O. die bezüglichen Werthe:
No. 208. S. 395. Der Inhalt dieses §. und seiner Zusätze muss in der neuesten Zeit bedeutend modificirt werden. Namentlich hat Encke in einer akademischen Abhandlung über die Massen und Dichtigkeiten sämmtlicher grösseren Planeten bemerkt, dass die der Sonne näheren Planeten Mercur, Venus, Erde und Mars nahebei dieselbe Dichtigkeit und zwar eine grössere = 1. die drei entfernteren Jupiter, Saturn und Uranus wieder nahe einerlei und eine kleinere Dichtigkeit = ¼ besitzen.
Was die, durch die Sonne auf den einzelnen Planeten hervorgebrachte Erwärmung betrifft[WS 1], so dürfte deren Grad auch von der chemischen Beschaffenheit dieser Weltkörper abhängen. Die in Zusatz 4. hierüber gemachten Bemerkungen können daher nur unter der Voraussetzung gelten, dass alle Planeten identische Bestandtheile haben.
No. 209. S. 395. Bis vor einigen Jahren erklärte man allgemein die Erscheinung der Sonnenflecken durch die Hypothese von Oeffnungen, welche sich in der, den dunkeln Sonnenkörper umgebenden Photosphäre befänden. Hiernach konnte von einem Schwimmen der Sonnenflecken, wie im Text, nicht die Rede sein. Nach den neuen spectroscopischen Untersuchungen der Sonne wird ein solches Schwimmen nicht nur möglich, sondern selbst wahrscheinlich.
No. 210. S. 395. Nach §. 47., Zusatz 7. des zweiten Buches ist der Verlust der Bewegung, welcher bei einem ungleichförmigen Widerstande stattfinden würde, während der Zeit t proportional wenn T die Zeit bezeichnet, in welcher die ganze Bewegung durch einen gleichförmigen Widerstand verloren gehen würde.
Bezeichnet man nun den ersteren Widerstand durch R', den letzteren durch R, so ist ferner nach §. 57. des erwähnten Buches R' : R = Dichtigkeit des Jupiters : Dichtigkeit des Mittels = 860 : 1, nach dem Obigen R' : R = t : T + t; also t : T + t = 860 : 1. Während der Zeit T lege der Jupiter wirklich einen Bogen A zurück, ferner werde der von der Sonne aus gesehene Durchmesser des Jupiters = 37″ = D gesetzt; alsdann wird nach §. 57. R' : R = A : 8/3D = 860 : 1, woraus A = 23° 34′ 18″ folgt, zu dessen Durchlaufung der Jupiter 283 Tage braucht. Es ist also T = 283, t = 30 und daher nahe = .
No. 211. S. 396. Statt der Proportion A : 8/3D = 860 : 1 in der vorhergehenden Bemerkung, woraus A = 23° 34′ 13″ und T = 283 Tagen folgte, haben wir jetzt die folgende A : 8/3D = 860 · 75 Billionen : 1; daher T = 75 Billionen mal 283 Tage = 58200000000000 Jahre und wenn t = 1000000 Jahren gesetzt wird, , weit kleiner als .
No. 212. S. 396. Nach Hansen ist a. a. O. der Halbmesser der Sonne
| =112,06 Halbm. ♁, = 112,06 · 858 g. M. = 96147, 5 g. M. = R. |
Entfernung ♄ von ☉ = 197000000 g. M = Δ' mithin .
Ist der Abstand des gemeinschaftlichen Schwerpunktes der Sonne und des Jupiters vom Mittelpunkte der Sonne = x; so haben wir zur Bestimmung von x, die Gleichung
| Nach Hansen | |||
| 1067 · x | = 1 · (Δ – x) | ||
| also | x | = 100678 | |
| und | x – R | = 4530,5 g. M. |
Ebenso ergiebt sich der Abstand x¹ des gemeinschaftlichen Schwerpunktes von ☉ und ♄, vom Mittelpunkte der Sonne aus
| Nach Hansen | |||
| 3021 · x¹ | = Δ¹ – x¹ | ||
| also | x¹ | = 65159 | |
| und | R – x¹ | = 30988,5. |
Für ☿ ist, nach Astr. Nachr. Nr. 488. die Masse der Sonne = 4865751, wenn die Masse des ☿ = 1 gesetzt wird, ferner ΔII = 8000000 g. M.
| Für ♀ | Masse | der | Sonne | = 401847 | ΔIII | = 15000000 g. M. |
| „ | „ | Venus | = 1 | |||
| 401857 · xIII | = ΔIII – xIII | |||||
| xIII = 37,3 g. M. | R – xIII | = 96110,2 g. M. | ||||
| Für ♁ | Masse | der | Sonne | = 354936 | ΔIV | = 20,666800 g. M. |
| „ | „ | Erde | = 1 | |||
| 354936 · xIV | = ΔIV – xIV | |||||
| xIV = 58,2 g. M. | R – xIV | = 96089,3 g. M. | ||||
| Für ♂ | Masse | der | Sonne | = 2680337 | ΔV | = 31500000 g. M. |
| „ | „ | Mars | = 1 | |||
| 2680337 · xV | = ΔV – xV | |||||
| xV = 11,8 g. M. | R – xV | = 96135,7 g. M. | ||||
| Für |
ist Masse | der | Sonne | = 17918 | ΔVI | = 396,500000 g. M. |
| „ | des | Uranus | = 1 | |||
| 17918 · xVI | = ΔVI – xVI | |||||
| xVI = 22127,3 g. M. | R – xVI | = 74020,2 g. M. | ||||
| Für ♆ | ist Masse | der | Sonne | = 20570 (Astr. Nachr. Nr. 921) | ||
| „ | des | Neptun | = 1 | ΔVII | = 621,700000 | |
| 20570 · xVII | = ΔVII – xVII | |||||
| xVII = 30222,2 g. M. | R – xVII | = 65925,3 g. M. | ||||
No. 213. S. 397. Statt „der Welt“ muss hier wohl „des Sonnensystems“ gelesen werden.
No. 214. S. 398. Nach §. 15. ist die Masse des Jupiters = , für die Masse der Sonne = 1; nach Hansen am angeführten Orte wird dieser Bruch . Eben so gross ist die Schwere gegen beide Körper, bei gleichen Abständen, bei ungleichen Abständen ist die Schwere den Quadraten der Abstände umgekehrt proportional. In der Conjunction von ♃ und ♄ wird ihr gegenseitiger Abstand = 197000000 – 107500000 = 89500000 und daher dieser Abstand des ♄ vom ♃, zum Abstande des ♄ von ☉ wie 895 : 1970 sehr nahe = 4 : 9. Das zusammengesetzte Verhältniss, in welchem die Schwere des Saturns gegen den Jupiter zu seiner Schwere gegen die Sonne steht, ist mithin
| Nach Hansen | ||
| oder | 81 : 16 · 1067 | 81 : 16 · 1054 |
| nahe | 1 : 211 | 1 : 208 |
No. 215. S. 398. Unmittelbar erhalten wir dieses Verhältniss, unter Anwendung des Werthes 3500 nach Hansen, statt des im Texte gebrauchten 3021, = 16 : 81 : = 16 : 81 : 181440. Das folgende Verhältniss wird in diesem Falle 65 : 181440 = 1 : 2791.
So. 216. S. 399. Von einer absoluten Ruhe der Fixsterne kann jetzt füglich nicht mehr die Rede sein, seitdem man bei einer grossen Anzahl derselben die sogenannte eigene Bewegung aufgefunden hat.
No. 217. S. 399. Nach dem Vorgange Bessel’s und W. Struwe’s, denen es gelungen ist, an zwei Sternen eine wenn auch geringe jährliche Parallaxe nachzuweisen, ist eine ähnliche Untersuchung bei anderen Sternen gelungen. Bei der Berechnung der Bahnen von Doppelsternen hat man ferner die Anziehung derselben auf einander mit Erfolg in Anwendung gebracht, woraus man mit Wahrscheinlichkeit schliessen darf, dass die einzelnen Fixsterne auch auf unser Sonnensystem im ganzen eine Wirkung ausüben dürften. Hieraus folgt aber noch nicht, dass sie auch auf die einzelnen Planeten eine gesonderte und daher wahrnehmbare Wirkung ausüben werden.
No. 218. S. 399. Setzt man die halbe grosse Axe der Marsbahn = a, die halben grossen Axen der ♁, ♀ und des ☿ = a', a'', a''', die rückläufige, hundertjährige Bewegung des Aphels von ♂, wie im Text, = 33′ 20″; so hat man nach Hansen a. a. O.
| 100j. r. Bew. d. Aph. | |||||||
| log a | = 0,18290 | log(33′20″) | = 3,30103 | ||||
| log a' | = 0,00000 | 3/2log | = 9,72565 | ♁ | 17′ | 46″ | nahe wie im Texte. |
| log a'' | = 9,85934 | 3/2log | = 9,51466 | ♀ | 10 | 54 | |
| log a''' | = 9,58781 | 3/2log | = 9,10737 | ☿ | 4 | 16 | |
| jähr. Bew. d. Aph. | 100jähr. B. d. Aph. | |||||
| für | ♂ | 15,″46 | 25′ 46″ | von | W. n. O. | rechtläufig, |
| „ | ♁ | 11,25 | 18 45 | „ | W. n. O. | „ |
| „ | ♀ | 3,24 | 5 24 | „ | O. n. W. | rückläufig, |
| für | ☿ | 5,81 | 9 41 | „ | W. n. O. | rechtläufig. |
No. 219. S. 399. Nach Hansen a. a. O. sind diese Werthe: für den Jupiter 9h 55m, für den Mars 24h 37m, für die Venus 23h 21m, für die Erde 23h 56m, für die Sonne 25½ Tage, für den Mond 27 Tage 7h 43m.
No. 220. S. 400. 27½ Tage machen ungefähr 10/133 vom Jahre aus, und die Erde bewegt sich daher in jenem Zeiträume um 10/133 ihrer Bahn fort. Den gleichvielten Theil ihrer Umdrehungszeit x, in Bezug auf die Fixsterne, braucht die Sonne mehr, um in Bezug auf die Erde ihre Drehung zu vollenden. Aus = 27,5 folgt x = 25,6 Tagen.
No. 221. S. 401. Da nach der Tabelle in Schumacher’s Jahrbuch für 1837, pag. 261 7000 engl. Fuss = 1094,67507 Toisen, so werden 367196 engl. Fuss = 57300 Toisen.
No. 222. S. 401. Nimmt man aus den drei im Texte für 1° aufgeführten Werthen das arithmetische Mittel = 57140,3 Toisen, und führt hiermit die Rechnung durch, so ergiebt sich die Peripherie = 123423048 par. Fuss, der Halbmesser = 19643390 par. Fuss.
No. 223. S. 401. Beim Nachrechnen fand ich die hier im Text aufgeführten Zahlen etwas verschieden, jedoch ist der Unterschied so gering, dass das Endresultat unverändert bleibt. Ich finde, wenn ich den gesuchten, in eine Secunde zurückgelegten Bogen durch x bezeichne und den Erdradius r = 19615800 Fuss setze, aus 2rπ : x = 86164 : 1, x = 1430,41 Fuss. Ferner wird sin versus x = = 0,0521536 Fuss = 7,51012 Linien. Unter dem Aequator in A sei c die Centrifugalkraft, alsdann ist dieselbe dem Radius CA = r proportional. Unter der Breite φ in P wird die c parallele Centrifugalkraft c' dem Radius DP = r cosφ proportional. Zerlegt man nun c' in zwei Seitenkräfte, die eine längs P, die andere auf CP senkrecht, so wird erstere = c' cos φ = cos φ², und da cos φ² = 0,43325, c cos φ² = 7,510 · 0,43325 = 3,254. Das Verhältniss 2177,254 : 7,510 wird, wie im Text, gleich 289 : 1.No. 224. S. 402. Nach der in der Bemerkung 74 zu S. 217, ausgeführten Rechnung findet sich die Anziehung des Punktes Q gegen das Sphäroïd durch das Integral dx, wo QT = x, QR = z, QC = PC = b, TR = y ist. Es ist nun im vorliegenden Falle z² = x² + y² = x² + (2bx – x²) = ,
oder
Für die entsprechende Kugel ist z = und so dx
oder 2. dx = ⅔b, und nach Gleichung 1. und 2. das gesuchte Verhältniss
3. : ⅔. Nach der Voraussetzung ist a : b = 101 : 100, also ; ; Arc. sin. = 16° 8′ 18,″9 = 58098,″9. Führt man die numerische Rechnung weiter, so wird = 101,50251; · Arc. sin. = 100,83038, das Verhältniss 3. 0,67213 : ⅔ = 201639 : 200000 = 126,02 : 125.
No. 225. S. 402. In diesem Falle geht nach der obigen Figur, indem wir AP = x', VW = y', AW = z' setzen, das Integral über in
Die log. sind hier hyperbolische, und für die entsprechende Kugel wird hier 5. = ⅔a; also nach Gl. 4. und 5. das gesuchte Verhältniss
Da ferner = 99,502488, log = 0,2826078, so wird das Verhältniss 6. [– 99,502488 + 100,163650] : ⅔ = 198348 : 200000 = 125 : 126,02.
No. 226. S. 402. Setzt man die durch die Kugel, die Erde und das Sphäroïd auf A ausgeübte Schwerkraft respective gleich K, E, S; so hat man K : E = 101 : 100, E : S = 101 : 100, also K : E = E : S, oder E = = 125,5…
Nr. 227. S. 403. Bezeichnet man die Schwere in einem unbestimmten Orte X auf der Erde durch F(X), auf der Kugel durch φ(X), auf dem Sphäroïd durch ψ(X); so hat man F(Q) : φ(Q) = 126 : 125, φ(A) : F(A) = 126 : 125,5, φ(Q) : φ(A) = 100 : 101; mithin F(Q) : F(A) = 126 · 126 · 100 : 125 · 125,5 · 101 = 501 : 500.
No. 228. S. 404. Nach Hansen a. a. O. ist 2a = 38,″4, 2b = 35″,6, a : b = 14 : 13.
No. 229. S. 405. Stellt die nebenstehende Figur ¼ des Spharoïds vor, ist A'C = a die halbe grosse, PC = b die halbe kleine Axe; so verhält sich die Schwere unter dem Aequator in A' zu der unter dem Pole in P, wie b : a, und zu der in B wie b : r, wo CB = r. Mithin ist, wenn α die Schwere in A', β die Schwere in B bezeichnet, α proportional , β proportional und so die Zunahme der Schwere von A' bis B, oder β bis α proportional . Ist nun CA = x, AB = y, die Breite BCA' = φ, so haben wir = 1 und weil y = r sinφ, x = r cosφ, =1. Setzt man nun b² = a² (1 – e²), wo e² nothwendig sehr klein ist, so wirdoder … oder mit grosser Annäherung , d. h. proportional sinφ².
No. 230. S. 405. Vernachlässigt man die höheren unbedeutenden Glieder, so wird der Ausdruck des Meridiangrades m = α – βcos2φ, wo α und β constant sind, mithin für φ = o, m' = α – β und m – m = β (1 – cos2φ) = βsin. ver. 2φ = 2βsinφ².
No. 231. S. 405. Da für Paris die Länge des Pendels l = 3 Fuss 85/9 Linien = 440,550 Linien, so wird die Länge des synchronischen Pendels unter dem Aequator: l' = · 440,555 = 439,468, also l – l' = 1,087 Linien.
No. 232. S. 409. Bezeichnet a und b bezüglich den Halbmesser am Aequator und am Pole, so ist nach §. 23. a : b = 230 : 229, welche Proportion der Berechnung der Tabelle im gegenwärtigen §. zum Grunde liegt und womit Richer’s Resultat nahe übereinstimmt. Es wird also a – b = a und da = 3923,16 Meilen (§. 23.) a = 3932 M. a – b = 171/10 M. wie §. 23.
No. 233. S. 409. Bekanntlich wird gegenwärtig bei allen astronomischen Rechnungen die Nutation gehörig berücksichtigt.
No. 234. S. 409. Nach Hansen a. a. O. beträgt die tägliche Bewegung des Perigeums 6′ 41,″0 von Westen nach Osten, die tägliche Bewegung der Knotenlinie 3′ 10,″64 von Osten gegen Westen.
No. 235. S. 410. Nach Hansen a. a. O. beträgt die rückläufige Bewegung der Knotenlinie des Mondes in 100 Jahren 5 Umläufe 134° 9′ 57,″5 = 1934,°41, die siderische Umlaufszeit der Erde um die Sonne 365,d25, die des Jupiters um die Sonne 4332,6, die Umlaufszeit des Mondes um die Erde 27,32 Tage, des vierten Trabanten um ♃ 16,7 Tage. Wir haben daher, wenn wir die Bewegung der Knoten des 4. Trabanten in 100 Jahren durch x bezeichnen:
| x : 1934,″41 = | |
| log (16,7 · 365,25²) | 6,34790 |
| log 1934,41 | 3,28659 |
| Compl. log (27,32 · 4332,6²) | 1,29122 |
| log x | 0,92571 |
No. 236. S. 411. Man kann auch so sagen: Die Variation x des 4. Trabanten verhält sich zur Variation V unseres Mondes, wie die jährliche Bewegung der Mondsknoten zur jährlichen Bewegung der Knoten des Trabanten, und wie die Umlaufszeit des Mondes zur Umlaufszeit des Trabanten. Nun ist die Bewegung der Mondsknoten in 100 Jahren = 1934°,41, also in 1 Jahre = 19°,3441 = 69639″, die Bewegung der Knoten des Trabanten in 100 Jahren = 8° 26′ = 30360″, mithin die einjährige = 303″,6. Die Variation
| nach Newton | nach Hansen | |
| V | 33′ 14″ = 1994″ | 39′ 30″ = 2370″ |
| mithin | x : V = | |
| x = 5″,31 | x=6″,3. | |
No. 237. S. 416. Nach den Werthen von Hansen a. a. O. wird dieses Verhältniss (27,321661)² : (365,25637)² = 1000 : 178312 = 1 : 17812/40.
No. 238. S. 417. Bringt man hier den in der vorstehenden Bemerkung aufgeführten Werth 178,312 in Anwendung, so erhält man das Verhältniss 1: 636619,3.
No. 239. S. 418. (Fig. 191.) Es ist Δ Ppq ∼ PKT, und weil pq = Kk, so wird Kk = . Ferner FK · Kk = · Pp, d. h. weil Pp constant ist, FK · Kk proportional .
No. 240. S. 418. EL ist proportional PK · TK = PT sin PC · PT cos PC, und wird daher ein Maximum für PC = 45°. Ferner wird in diesem Falle FK · Kk = ½ · Pp = ½TP · Pp.
No. 241. S. 419. Die Geschwindigkeit des Mondes ist dem Increment (Moment) der Fläche proportional, also im Mittel = 11915 · a, wo a irgend eine Constante bezeichnet. Mithin wird die Geschwindigkeit im Texte, welche 100/11915 von der des Mondes gleich ist, nun 100 · a und so die in den Syzygien und den Quadraturen stattfindende Geschwindigkeit respective 11965 · a und 11865 · a.
No. 242. S. 419. Es ist nämlich FKCG : GCF = (GC + FK)CK : GC · CT = CT² – KT² : CT² = PK² : PT² = PT · Pd : PT² = Pd : PT.
No. 243. S. 419. Nach dem Vorhergehenden ist nämlich das Moment dieser Fläche proportional
| 109,73 + Pd, | für | den | Radius | PT | = 100, | oder |
| 109,73 + Pd | „ | „ | „ | = 1 | „ | |
| 219,46 + 2Pd | „ | „ | „ | = 1. |
Nun ist Pd = sinus versus PC und 2 Pd = Pd' = sinus versus PCP' = sinus versus 2 · PC.
No. 244. S. 420. Setzt man die stündliche Bewegung = dv, den Abstand = r und die beschriebene Fläche = f; so wird f = ½r²dv und r = .
No. 245. S. 420. Setzt man die Geschwindigkeit a'c' = v, den Radius des osculirenden Kreises a'd = r und die Anziehung b'c' = k; so ist offenbar sehr nahe 2kr = v² und , und offenbar der Krümmung proportional. Für ab = a'b' oder ac = a'c' und beide unendlich klein, kann man bc = sin bac oder = tang bac und b'c' = sin b'a'c' oder = tang b'a'c' setzen.No. 246. S. 420. In der Entfernung N ist die Schwere des Mondes gegen die Erde = 178725, mithin in der Entfernung AT = . Die Kraft der Sonne wirkt in den Syzygien derjenigen der Erde entgegen und ist im Abstande N von der Erde = 2000; daher im Abstande AT = . Mithin wird die ganze erziehende Kraft proportional oder auch, indem man durch N² dividirt, proportional . Weil aber sehr nahe AT = CT, wird und ; mithin obige Kraft sehr nahe proportional ; oder 178725CT² · N – 2000AT² · CT. Aehnlich für die Quadraturen.
No. 247. S. 422. (Fig. 193.) Wir wollen der Kürze wegen
| die | Krümmung | der | Ellipse | in | A | und | C | durch | EA, EC | |
| „ | „ | „ | Figur | Tpa | „ | a | „ | C | „ | Ba BC |
| „ | „ | des | ersten | Kreises | „ | KA | ||||
| „ | „ | „ | zweiten | „ | „ | KC | ||||
bezeichnen. Denkt man sich nun aus T mit TA einen Kreisbogen geschlagen, welcher durch A und a gehen wird und hierauf von A und a aus auf der Ellipse und Bahn gleichzeitig beschriebene kleine Stücke v und v' abgetragen, so dass in beiden Fällen der Körper durch die anziehende Kraft der Erde ihr um gleiche Stücke e näher gebracht sein würde; so ist dem Unterschiede der Krümmungen der Bahn in a und des Kreises in a, oder Ba – Ka proportional (Bem. 245.) Ferner ist dem Unterschiede der Krümmung der Ellipse in A und desselben Kreises, oder EA – KA proportional. Wir haben daher
Auf ähnliche Weise ergiebt sich das letzte Verhältniss im Texte
Ferner ist KA proportional , KC proportional , EA ist dem Radius des osculirenden Kreises in A und EC den Radius des osculirenden Kreises in C umgekehrt proportional. Der erste Radius ist aber = , der letztere = , also
No. 248. S. 422. Aus Proportion 2. folgt nämlich
hieraus
Ferner aus Proportion 4.
hieraus und aus 1a.
oder
hieraus und aus 3.
Durch die Verbindung der Proportionen 7. und 11. erhalten wir endlich
Man hätte übrigens auch die Verhältnisse EA : Ba und EC : BC unmittelbar nach §. 84, Zusatz 3 des ersten Buches auf folgende Weise finden können. Setzte man statt des dortigen
| A | hier | TA |
| T | „ | TC |
| R | „ | |
| F | „ | CTP |
| G | „ | CTp; |
so würde das Verhältniss der Kräfte für E und B in den Punkten A und a und das Verhältniss der Geschwindigkeiten CTP : CTp; mithin EA : Ba = oder auch
Vertauscht man hier
| TA | mit | TC, |
| A | „ | C |
und umgekehrt, so erhält man unmittelbar
Aus diesen beiden Gleichungen 13 und 14 würde man leicht, durch Benutzung der Proportionen 2, 3 und 4, die Proportion 12 wieder herleiten können.
No. 249. S. 423. Dem Winkel CTP in der Ellipse entspricht die mittlere Bewegung CTP' im Kreise, und es ist daher tang CTP : tang CTP' = PQ : P'Q = AT : TC = 69 : 70.No. 250. S. 423. Bestimmt man einen Winkel CTP'' so, dass tang CTP'' = tang CTP so wird, weil tang CTP = tang CTP', tang CTP'' = tang CTP'.
No. 251. S. 429. (Fig. 196.) Aus fg = in 5. folgt nach 4. , d. h. T, G und g liegen in gerader Linie und es ist fTg = FTG. Allgemein ist aber sin fTg = sin FTG = sin fgT : sin FGT näherungsweise = , weil genähert fgT = FGT. Es ist aber wirklich (nach 6.) fg = , d. h. das fg in 5. muss durch multiplicirt werden. Demnach wird statt
No. 252. S. 430. Man setze die Radienvectoren in den Quadraturen, Octanten und Syzygien respective gleich q, o, s, die Winkelgeschwindigkeit allgemein = dv, die jenen entsprechenden Zeitelemente gleich t(q), t(o), t(s); alsdann haben wir nach dem Frühern (§. 30.) q²dv : s²dv = 10973 : 11073; also weil o²dv = ½(q² + s²)dv, o²dv : = 11023 : 50. Jene Verhältnisse der Flächenelemente würden für gleiche Zeitelemente gelten, wogegen bei verschiedenen Zeitelementen diese den ersteren umgekehrt proportional sind; demnach t(o) : = 11023 : 50.
No. 253. S. 431. In derselben Zeit, wo der Mond in seiner Bahn den Weg PM zurücklegt, beschreibt er, vermöge der während dieser kurzen Zeit als constant zu betrachtenden Sonnenkraft 3 · JT den Weg SM und dieser ist alsdann 3 · JT · Q², wenn t jene kleine Zeit bezeichnet.
No. 254. S. 431. Es verhält sich die übrigbleibende Bewegung zur ganzen Bewegung, wie 11023² : 11073², d. h. wie (11073 – 50)² : 11073² und wenn man 50² gegen 11073² vernachlässigt, beiläufig
woraus die Verhältnisse 100 : 10973 und 100 : 11073 im Text unmittelbar hervorgehen.
No. 255. S. 431. Man setze den Winkel, welchen der Mond im Octanten O in einer gegebenen Zeit zurücklegt = L, den derselben Zeit im Punkte P entsprechenden Winkel = L + x, endlich den der Syzygie A entsprechenden L + l. Ferner sei die, derselben Zeit entsprechende Bewegung des Knotens in O = N – d und in P = N. Da nun die letzteren Bewegungen dem Quadrat der Zeiten proportional sind, so wird N – d : N = L² : (L + x)² = L² : L² + 2Lx + x² oder, weil x in Vergleichung mit L sehr klein ist, genähertund hieraus N : d = L + 2x : 2x oder wieder genähert
Bezeichnet nun A die Bewegung des Knotens in der Syzygie A, und a deren Increment, so ist nach 2.
und nach 2. und 3. aN : d · A = l : x oder auch
Nun ist TE = AT · sin PTQ = AT · cos AP, also TE² – ½AT² = AT² cos AP² – ½AT² = ½AT² cos 2 · AP), und nach 5.
Nach der vorhergehenden Bemerkung (255) ist nun
ferner weil PQJ = 2 · PQ, nach §. 30 P : A = JF : 2AT und so,
ebenso
indem KF = TA sin vers. PK = TA sin vers. 2 · AP = TA sin vers. 2 · P'''Q und TF = TA cos 2 · AP = TA cos 2 · P'''Q. Aus 2. und 3. folgt p – p''' : a = (JF – KF)TF : 2AT² = 2TF² : 2 · AT² oder
ähnlich
und aus 4. und 5.
Da nun TF = TA · cos 2 · AP, TG = TA cos 2 · AP' = TA cos 2 (AO – OP') = TA cos 2(45° – AP) = TA sin 2 · AP, also TF² + TG² = TA², so wird aus 6. p + p' – p'' – p''' = a.
No. 257. S. 432. Es ist nämlich Aa : ZY = AT : AZ, wo Aa und AT gegebene Grössen sind.
No. 258. S. 433. Setzt man die mittlere Bewegung des Knotens im Orte N = m(n), in der Quadratur, wo sie am grössten und = 39°,6355 ist, = m(g), endlich die Bewegung der Sonne = 360° = m(s); so ist m(s) : m(g) = 360 : 39,6355, m(g) : m(n) = AT² : AZ², mithin m(s) : m(n) = 360 · AT² : 39,6355AZ² = 9,0827666AT² : AZ² = α · AT² : AZ², wo der Kürze wegen 9,0827666 = α gesetzt ist. Ferner wird m(s) : n(s) + m(n) = α · AT² : α · AT² + AZ² und daher, wenn t(s), t(n) die, den Bewegungen m(s), m(n) respective entsprechenden Zeiten bezeichnen, weil m(n) der m(s) entgegengesetzt ist und daher t(s) durch t(n) verkürzt wird, t(s) : t(s) – t(n) = α · AT² + AZ² : α · AT².
No. 259. S. 433. Es ist
da aber ATa = ½Aa · AT und Aa : YZ = AT : AZ, also Aa = ; so wird dZ · ZY : ATa = dZ · ZY : ½ = dZ · BZ : ½AT² und es geht die Proportion 1. über in
dZ · ZY entspricht t(n), d. h. den durch die Knotenbewegung hervorgebrachte Decrement der Zeit, während der durch ATa dargestellten Zeit; NdZ stellt das, dem Sector ATN entsprechende Decrement dar und da NATN die ganze unverkürzte Zeit darstellte, so wird NATN – NdZ die ganze, vermöge der Knotenbewegung verkürzte Zeit darstellen.
No. 260. S. 434. Wir haben im Text aZ : AZ = AZ² : α · AT² + AZ² = t(n) t(s), also auch aZ · ZY : AZ · ZY = t(n) : t(s) oder aZN : AZN = T(n) : T(s), wo T(n) und T(s) die Summen aller t(n) und t(s) bezeichnen. Es wird auch aZN · AZN – aZN = aZN : NAa = T(n) : T(s) – T(n).
No. 261. S. 434. (Fig. 197.) Setzt man TZ = x, ZA = y, Za = y : TA = rα wie vorhin, α' = α + 1; so ist nach der frühern Proportion. (Bem. 260.) aber y² = r² – x², also y' =
Hiernach wird
Der Halbkreis ist = ½r²π, mithin verhält sich NAn : NeFn = 1,57090 : 0,11869 = 794,1 : 60.
No. 262. S. 437. (Fig. 199.) Weil TH² = TS · TK ist, wird SK : ST = SK : = TK · TK : TH² = (TK – TS)TK : TH² = TK² – TH² : TH² = (TK + TK)(TK – TH) : TH² endlich TK : ST = MH · HK : TH².
No. 263. S. 437. (Fig. 199.) Setzt man nämlich FG = Y, BG = y, GT = x, HT = h, KT = a; so ist y² = (a² – x²), Y² = a² – x², mithin .
No. 264. S. 438. (Fig. 199.) Nach 1. wird nämlich TH : TK = .
No. 265. S. 438. (Fig. 199.) Setzet man, wie in Bem. 264. BG = y, FG = Y, TG = x, ferner FTG = β und FTB = α – β = γ; so ist allgemein tang α = , tang β = , tang γ = . Wenn aber HT = b und KT = a gesetzt wird, ist Y = y und y² = (a² – x²), also tang γ = b(a – b). Bezeichnet man nun die, dem grössten Werthe von γ entsprechenden Werthe durch einen Accent, so folgt aus d · tang γ = o, a²b (a + b)x'² = o, also x' = a, y' = b, Y' = a, tang α' = , tang β' = , tang γ' = . Ferner tang α' · tang β' = 1, also α' = 90° – β', = 45° endlich tang γ' = , sin (α' – β') = . Eben so aus tang (α + β) = , sin (α' + β') = und so sin (α' – β') : sin (α' + β') = a – b : a + b = : 1 = sin γ' : 1.
No. 266. S. 438. Die mittlere tägliche Bewegung der Sonne ist = 59′8,″3, daher ihre mittlere stündliche Bewegung Δ ☉ = 147″,8. Setzen wir ferner die mittlere stündliche Bewegung der Knoten in den Quadraturen = Δ ♌(q); so haben wir nach Anmerkung 1. Erster Fall, TS : SK = Δ ☉ : Δ ♌(q). Aus der Proportion TH : TK = folgt aber mittelst Gl. 1. TS : TK = 9,0827646 : 40,0827646, TS : SK = 9,0827646 : 1, also Δ ♌(g) = = 16″3. Nach der vorhergehenden Bem. 265. haben wir sin γ' = und da a = KT, b = HT und TK : TH = 19,6524761 : 18,6524761 sin γ' = 1/38,3049522, γ' bedeutet aber nach der vorigen Bemerkung die grösste Bewegung des Knotens in den Octanten, und bezeichnen wir diese stündliche Bewegung durch Δ ♌(o), so haben wir Δ♌(o) = 1° 29′ 45″ ein wenig von dem Werthe im Texte abweichend.
No. 267. S. 439. (Fig. 200.) Es ist GT sin GTg = Gg = · sin GPg · gP und &sin GPG : sin GTg = = GT · Pp : Pg², indem Pg = PG gesetzt worden ist.No. 268. S. 440. (Fig. 200.) Setzt man der Kürze wegen die im Zusatz 2 gefundene Veränderung der Neigung während eines Monats = V, so ist V : 33″,2 = AZ · TZ · QAqa : 2Mp · AT² oder : 33″,2 = AZ · TZ · : 2 · AT² und weil Mp die stündliche Bewegung des Mondes auf der Peripherie QAqa ist, die mittlere stündliche Veränderung der Neigung.
| Ferner ist unmittelbar | = sin PGp, | für | den | Radius | = 1 |
| = | „ | „ | „ | = AT |
= sin ATn, = cos ATn, mithin = ½sin ATn · cos ATn = ¼ sin 2 · ATn.
No. 269. S. 440. (Fig. 200.) In diesem Falle trifft N mit Q zusammen, es geht daher AZ in AT, TG in TK über und wir erhalten JT · TG = AT · sin pTQ · AT · cos pTQ = ½AT² sin 2pTQ, so wie = AT · sin 2pTQ.
No. 270. S. 441. Um die Summe der im Text aufgeführten Sinusse zu finden, wollen wir uns den Quadranten ½π in n gleiche Theile getheilt denken, wo n eine grosse Zahl, hier 1771/6 bezeichnet; alsdann haben wir die Reihe bis zu summiren. Setzen wir nun = x, so wird die gesuchte Summe S = sin x + sin 2x + sin 3x + . + … + sin νx, wo νx = π = π – π, (ν – 1)x = π = π – π. Setzen wir statt der Sinusse die ihnen entsprechenden Exponentialfuncionen, so wird für i = ,
Da aber sin (ν – 1) x = sin (π – π) = sin ; sin νx = sin sin x = sin ; cos x = cos , so wird S = und = . Da nun n sehr gross, also sehr nahe = o vorausgesetzt sind, so kommt der vorstehende Quotient der Form nahe. Um den Grenzwerth desselben für n = ∞ zu finden, setzen wir = k; alsdann geht jener Quotient über in S = d. h. für k = o oder n = ∞, S = wie im Text. Ferner wird = sin 5° 1′ = 874/10000 und 278/10000 · 5878″ = 163″.
No. 271. S. 442. Setzt man in §. 38., Zusatz 3. die stündliche Aenderung der Neigung = ν, dort wie hier die Neigung selbst = i, den Winkelabstand der Knoten = Δ; so ist
| dort | hier |
| ν = · 33″,2 | Hh = C sin i sin 3Δ |
wo r und C constant sind. Mithin sind ν und Hh derselben Grösse sin i sin 2Δ, und wenn sin 2Δ als constant vorausgesetzt wird, sin i proportional: Hh wird daher in gleichem Sinne wie sin i zunehmen.
No. 272. S. 444. Der Werth der grössten Mittelpunktsgleichung der Sonne, für den mittlern Abstand der Erde = a, ist im Text = 1° 56′ 20″ = M angesetzt, wobei wir bemerken, dass Hansen a. a. O. M = 1° 55′ 27,″6 hat. Für den Abstand a + x, wird M' = M + Δ'M = M · ; M'' = M + Δ''M = M · also Δ'M : Δ''M = 2 : 3 und Δ''M = 3/2Δ'M. Wenn nun Δ'M die wahre Aenderung von M und Δ''M die hypothetische Aenderung desselben ist, so können wir M + Δ'M = 1° 56′ 20″ oder für M = o, Δ'M = 1° 56′ 20″ setzen und erhalten dann M'' = Δ''M = 3/2(1° 56′ 20″) = 2° 54′ 30″.
No. 273. S. 444. Setzt man die grösste Gleichung der mittlern täglichen Bewegung des Apogeums = ΔAp., die des Knotens = ♌, so hat man, auch Hansen a. a. O.
| ΔAp. | : 2° 54′ 30″ = | 6′41,″0 rechtl. | : 59′ 8,″3 |
| Δ♌ | 3′10,64 rückl. |
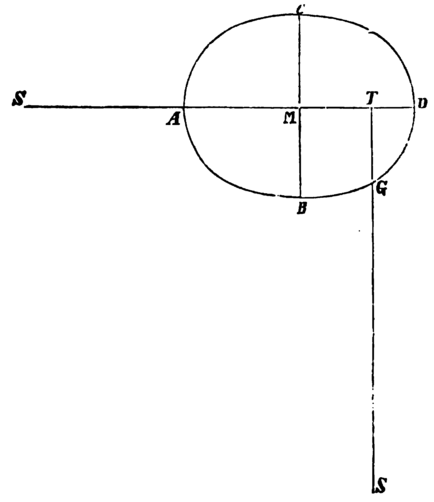
No. 274. S. 444. Es sei ACDB die Mondbahn, T die Erde, A das Apogeum des Mondes, S die Sonne und deren Abstand von T im Mittel ST = a. Die halbe grosse Axe der Mondbahn sei AM = α, ihre halbe kleine MB = β, die Excentricität MT = αε, also AT = α(1 + ε) und SA = a — α(1 + ε). Ferner wird die Ordinate TG = α(1 - ε²) und SG = a — α(1 - ε²) also TG < AT, SG > AS. Wenn daher der Mond sich im Punkte A befindet, wird die Wirkung der Sonne auf ihn grösser sein, wenn die Sonne sich in der Richtung AD befindet, als die von S ausgehende Wirkung auf den in G befindlichen Mond, wenn die Sonne sich in der auf AD senkrechten Richtung TG befindet und zwar verhält sich die erste Anziehung zur zweiten wie .
No. 275. S. 445. Für die Excentricität der Erdbahn = 0,0168 wird der grösste Abstand der Sonne von der Erde = 1,0168, der kleinste = 0,9832; demnach die kleinste Gleichung = = 3' 34,"0, die grösste Gleichung = = 3' 56,"7.
No. 276. S. 445. Der für den mittlern Abstand a geltende Werth von 47" ändert sich in demselben Verhältniss, wie in der vorhergehenden Bemerkung und da die in dieser gefundene Aenderung 11" bei 3' 45" = 225" des mittlern Werthes, also etwa 1/20 letztem beträgt, so muss hier 45" um 2" steigen und sinken.

No. 277. S. 416. Man schlage aus D mit dem Radius DF einen Kreis, alsdann ist E das Apogeum des Mondes und ☾ sein Perigeum. Es sei α das Apogeum der Sonne, P das Perigeum, ☉ der Ort der Sonne.
Nach der Voraussetzung ist dDE = DCB = 2 · ☉E, EDC = 180° — 2 · ☉E, FDE = ☉E — PE. (Voraussetzung im Text), also addirt EDC + FDE = CDF 180° — ☉E = PE. Es ist aber PE☉α = 180°, mithin 180° = ☉E — PE = CDF = α☉ = 360" — α☾PEF☉ und α☾PEF☉ = Winkelabstand ☉ von ihrem Apogeum α = v (wahr. Anomalie ☉), mithin CDF = 360° — v.
No. 278. S. 446. Nach Hansen a. a. O. ist die mittlere tägliche Bewegung der Sonne von ihrem Perigeum = 59' 8,"3, die mittlere tägliche Bewegung des Perigeums des Mondes = 6' 41,"0, daher die tägliche mittlere Bewegung der Sonne vom Perigium (Apogeum) des Mondes = 52' 27,"3. Es wird log = 4,55070 und log = 4,55002.
No. 279. S. 447. Es wird hier TC = 5505 · sin 12° 18' = 1172,73 und FD = 3/100 · 1172,3 = 35,2.

No. 280. S. 448. Am grössten wird die, durch die Bewegung des Mittelpunktes der Mondbahn in dem kleinen, zu DF gehörigen Kreise hervorgebrachte Veränderung des Mondortes erscheinen, wenn man die diametral entgegengesetzten Punkte F, F' des Mittelpunktes betrachtet, wo also FDF' diese von T aus gesehene Veränderung unterspannt. Dieselbe wird = Arc sin und da FF' = 70,4; TD = 100000 ist, so ist diese Veränderung = 2' 25".
No. 281. S. 447. Aus diesem Grunde hat wohl Tobias Mayer die noch heute in Anwendung kommende Regel aufgestellt, bei der Berechnung der Mondfinsternisse den Durchmesser des Schattens in der Gegend des Mondes um 1/60 zu vergrössern.

No. 282. S. 449. Es sei TH der Horizont eines Ortes T auf der Erde, S der Ort der Sonne, deren Hohe über dem Horizont STH = h sei, Z das Zenith. Befände sich die Sonne in Z, so würde ihre Kraft P zur Erhebung des Wassers in T nach dem Obigen zu bestimmen sein. Hieraus ergibt sich die längs TS wirkende Seitenkraft, nach dem Parallegramme der Kräfte, TM = P sin TZM = P sin h und hieraus die längs TZ, d. h. nach dem Zenith hinwirkende Seitenkraft TN = TM sin TMN = P sin h². Diese Kraft ist die gesuchte, wenn S nicht im Zenith Z, sondern in der Höhe h über dem Horizont steht. Sie ist daher proportional sin h² = ½(1 — cos 2h) = ½ sinus versus 2h.
No. 283. S. 450. Ein Theil dieses Satzes ist nicht recht klar dargestellt. Die dritte Fluth nach der Syzygie tritt etwa 36 Stunden später ein, in welcher der Mond sich rechtläufig im Mittel um 19° 35' und die Sonne nur 1° 28' bewegt, so dass ihr gegenseitiger Abstand 18° 7' beträgt. Legt man zu den vorstehenden 36 Stunden die sogenannte Hafenzeit in Bristol von 7 Standen, so kommen die im Text aufgeführten 43 heraus.

No. 284. S. 450. Befindet sich die Sonne in S, d. h. im Widderpunkte, ist L ein Solstitialpunkt, also SL = 90°, LL' = 18,°5, also der Mond um 18,°5 von der Quadratur entfernt; so ist sin L'a = sin 108°,5 sin 23° 27' = 22° 14'. Einmal ist die Kraft des Mondes in L' im Verhältniss cos L'a : 1 kleiner, ab wenn jener sich im Aequator befände. Ferner in demselben Verhältniss die Centripetalkraft und

daher auch die Centrifugalkraft in L kleiner als in a; mithin durch Zusammensetzung die Kraft des Mondes in L' im Verhältniss (cos L'a)² : 1 = (cos 22° 14')² : 1 kleiner als im Aequator.

No. 285. S. 451. Ist A der Ort des Mondes in der Syzygie, C der in der Quadratur, so hat man nach den Angaben im Texte, wenn die Erde sich in T befindet, die halbe grosse Axe TA = a = 70, die halbe kleine CT = b = 69. Wenn nun der Winkel ATa = CTc = 18,°5, aT = z, cT = a gesetzt wird, so wird unmittelbar nach den Formeln der Ellipse z² sin² 18,°5
z² = . Substituirt man hier die Werthe von a und b, so ergibt sich z = aT = 69,897530 nahe mit dem Text übereinstimmend. Mutatis mutandis, wird u² = und u = 69,098740.
No. 286. S. 451. Ich erhalte aus den Werthen im Texte die Verhältnisse 0,9827797 : 1 und 1,0172410 : 1. No. 287. S. 452. Nach Hansen a. a. O. ist, wenn D(s), D(e), D(m) bezüglich die Dichtigkeit der Sonne, der Erde und des Mondes bezeichnet, D(m) : D(s) = 0,619 : 0,252 = 2679 : 1000, D(s) : D(e) = 0,252 : 1,000, also D(m) : D(e) = 0,619 : 1,000 = 1000 : 1615 und im Gegensatz zum Text der Mond weniger dicht als die Erde. Vermittelst des Verhältnisses von D(m) : D(s) und der bezüglichen Werthe der scheinbaren Durchmesser 31' 7,"0 und 32' 1,"8 erhalten wir nach der Vorschrift im Texte die Kraft des Mondes zur Bewegung des Meeres zur Kraft der Sonne wie
No. 288. S. 252. Nach den Werthen im Text wird die Masse des Mondes zu derjenigen der Erde, wie
während nach Hansen 1 : 87,73 sich ergibt
No. 289. S. 453. Nach den im Text aufgeführten Werthen ist die Schwerkraft des Mondes = l, wenn die der Erde zukommende Schwerkraft durch t bezeichnet wird, l : t = ; l = 13329/39788 t nahe = ⅓t. Nach den neuern Werthen (Hansen a. a. O.) wird l : t = ; l = 1/6,561 t.
No. 290. S. 453. Aus der Gleichheit der statischen Momente
und daher
Nach den neuem Werthen wird 1 : 1 — x = 88,73 : 87,73.
No. 291. S. 454. Wir haben in den Syzygien den Abstand
| = 5929/30 | = 1799/30 | |
| in den Quadraturen den Abstand | = 605/6 | = 1825/30 |
| und daher in den Octanten den Abstand | = 1812/30. |
Dabei ist log 1825 — log 1812 = 0,00310 log 1812 — log 1799 = 3,00314, log 70 — log 69,5 = 0,00312 log 69,5 = log 29 = 0,00313.
No. 292. S. 454. Ich finde 39,788 · 100 : 1 · 365 = 1090 : 100 und daher statt 93 Fuss deren 24.
Nach den früher angeführten neuern Werthen hätten wir das Verhältniss 87,73 · 109 : 1 · 400 = 2391 : 100, und daher statt 93 Fuss deren 205,6 und den Unterschied der grossen und kleinen Axe 411 Fuss. Wohl verstanden, wenn der Mond flüssig wäre.
No. 293. S. 455. (Fig. 205.) Die Wahrheit dieser Behauptung würde sich leicht durch Raisonnement darthun lassen; man kann sie aber auch folgendermassen durch Rechnung beweisen. Es werde SNJ in n gleiche Theile getheilt, so dass jeder derselben = π = x sei, alsdann haben wir, für den Radius = 1, die beiden Summen:Durch Einführung der bekannten Exponential-Functionen wird
Hier ist, wie bekannt, i = , ferner folgt aus x = π, 2nx = 2π, (n — 1)2x = 2π — 2x, cos(n — 1)2x = cos 2x, cos 2nx = 1; mithin S = ¼ + ½(n — 1) = ½n. Was die Summe S' betrifft, so wird zunächst
+ ½ n = ½n, weil cos 2nx = 1 und cos (n + 1)2x = cos (2π + 2x) = cos 2x.
No. 294. S. 457.[WS 2] Bezeichnet Σ die Summe der Theilchen, so haben wir Σ(LX²) : Σ(JX²) = 1 : 2 (§. 44.) Σ(JX²) : Σ(AC²) = JX² : AC² (weil JX und AC constant sind), also Σ(LX² : Σ(AC²) = JX² : AC².
No. 295. S. 457.[WS 3] Bezeichnet Σ(JK) die Summe aller auf der Peripherie, Σ(A) die Summe aller in A befindlicher Theilchen, so hat man Σ(JK) : Σ(A) = JK² — 2 · CX² : 2 · AC² (Verh. 7.) Σ(A) : Σ(AC) = 2 : 1 (§. 44.), also (JK) : Σ(AC) = JK² — 2 · CX² : AC².
No. 296. S. 458. Zur Verdeutlichung des Inhalts dieses §. mögen folgende Sätze hier hinzugefügt werden.
I. Satz. Die Grösse der Bewegung eines Kreises, welcher mit constanter Geschwindigkeit um seinen Mittelpunkt getrieben wird, ist dem Cubus des Radius proportional. Setzt man Ca = r, so ist die Menge der kleinen Körper eines, Peripherie umgebenden sehr schmalen Ringes proportional 2rdr.

Ist die Winkelgeschwindigkeit constant, so wird die Geschwindigkeit in a proportional r; also das Differential der Grösse der Bewegung in a proportional 2r²dr · r = 2r²dr und die Bewegung des Kreises proportional
d. h. dem Cubus des Radius.
Zusatz 1. Würde alle Materie auf dem äussern Kreise AD vereinigt, wo CA = R; so wäre das Differential der Masse wie vorhin proportional 2rdr, die Geschwindigkeit in A proportional R, mithin das Differential der Grösse der Bewegung selbst proportional R · 2rdr und in diesem Falle die Grösse der Bewegung selbst proportional
Aus Gleichung 1. folgt für r = R die Grösse der Bewegung = ⅔R³.
Demnach verhält sich die Bewegung im letzten Falle zu der im erstem Falle stattfindenden Bewegung, wie
Zusatz 2. Die Bewegung eines Kreises verhält sich zur Bewegung eines sehr dünnen kreisförmigen Ringes, welcher mit gleicher Winkelgeschwindigkeit wie jener um den Mittelpunkt getrieben wird, wie die zweifache Materie des Kreises zur dreifachen des Ringes.
Für Aa = α ist nämlich dieses Verhältniss ⅔R³ : R2rdr
Zusatz 3. Werden Cylinder von gleicher Höhe um ihre Axen mit gleicher Winkelgeschwindigkeit gedreht, so verhalten sich die Grössen ihrer Bewegungen wie die Cuben der Radien ihrer Grundflächen.
Jeder dieser Cylinder ist nämlich als ein Aggregat gleich vieler, ihrer Grundfläche gleicher, Kreise anzusehen.
Zusatz 4. Wäre die ganze Materie des Cylinders auf dem Mantel vereinigt, so würde bei gleicher Geschwindigkeit die Grösse der Bewegung in diesem Falle sich zu der im vorigen Falle verhalten, wie 3 : 2. Dies folgt aus Zusatz 1.
Zusatz 5. Wenn bei unveränderter geringer Dicke der Wand, wie auch unveränderter Breite des innern Raumes, durch allmählige Abnahme der Höhe, die Wand selbst sich zusammenzieht und zuletzt in einen Ring oder eine Zone übergeht; so wird, wenn auf der in einen Ring zusammengezogenen Wand dieselbe Materie bleibt, welche früher innerhalb des ganzen Cylinders befindlich war, auch die Bewegung des Ringes unverändert bleiben und sich zur ursprünglichen Bewegung des Cylinders verhalten, wie 3 : 2.
Zusatz 6. Die Bewegung eines um die Axe herumgetriebenen Cylinders verhält sich zur Bewegung eines sehr dünnen, den Cylinder umgehenden Ringes, wie die doppelte Materie des Cylinders zur dreifachen Materie des Ringes.
Denkt man sich
| einen Cylinder C, | dessen Radius | = r | und | Materie | = m, |
| einen andern C', | „ „ | = r | „ „ | = μ | |
| und einen Ring R, | „ „ | = r | „ „ | = μ |
so hat man, wenn C, C', R zugleich die Bewegung dieser drei Körper bezeichnen, C : C' = m : μ, C' : R = 2 : 3 (Zusatz 5.), also C : R = 2m : 3μ.

II. Satz-Aufgabe. Um den Kreis GBJL ist das Quadrat ACMK und innerhalb des erstern die Figur GBEJL so beschrieben, dass für jede Ordinate DE
sei; man soll den Flächeninhalt dieser Figur mit dem des Kreises vergleichen.
Man setze DE = y', DF = y, HD = x, HJ = r, alsdann ist nach Proportion 1. y' : y = y² : r², also
Es ist aber y² = r² — x², mithin y' = und so jener Flächeninhalt von HBEJ.
Der erste Ausdruck auf der rechten Seite verschwindet für beide Grenzen x = o und x = r, das Integral auf derselben Seite ist gleich dem Flächeninhalt des Quadranten HBFJ. Setzt man daher den Flächeninhalt des ganzen Kreises = A, so wird der Flächeninhalt von
III. Satz. Wenn der eine Ring ACD gleichförmig um sein Centrum B, der andere EFKJ mit derselben Winkelgeschwindigkeit um den Durchmesser EK bewegt wird; so verhält sich die Grösse der Bewegung des ersten Ringes zu derjenigen des ihm gleichen zweiten Ringes, wie

π : 2. Ist der Radius beider Kreise = r, AC = EF, das Element der Winkelbewegung in beiden Fällen = dv; so wird das Element der Geschwindigkeit des Punktes C im ersten Ringe = rdv, im zweiten hingegen = FG · dv = ydv. Die Geschwindigkeit des Punktes C kommt allen Punkten desselben Ringes zu, und wenn wir daher dieselbe, mit der ihnen allen zusammen entsprechenden Materie = 2rπ multipliciren; so wird
die Grösse der Bewegung dieses Ringes, wenn derselbe einen ganzen Umlauf zurückgelegt hat.
Setzen wir im zweiten Ringe EFKJ das Element der Peripherie in F = ds, so ist ds · ydv das Element der Bewegung dieses Ringes, und es muss das Integral von dv, wie auch das von yds über die ganze Peripherie erstreckt werden. Für HG = x haben wir aber r² = x² + y² und ds² = dx² + dy² d. h. o = xdx + ydx und so ds² = dx² + also
Statt yds über die ganze Peripherie haben wir jetzt rdx von x = — r bis x = + r zu integriren, wodurch wir den Halbkreis ETK berücksichtigen. Damit auch die andere Hälfte KJE beachtet werde, haben wir das bestimmte Integral noch mit 2 zu multipliciren. Die Grösse der Bewegung des zweiten Ringes ist demnach
Aus den bisherigen 3 Sätzen folgt nun leicht die Wahrheit der in §. 46. ausgesprochenen Behauptung.
Denkt man sich nämlich in obiger Figur zum II. Satz den Cylinder und die Kugel mit gleichförmiger Bewegung um die Axe BL gedreht, so wird für den DN entsprechenden Kreis, nach II. Satz, die Grösse der Bewegung proportional DN³ = r³ und für den DF entsprechenden Kreis proportional DF³ = y³; mithin, wenn wir die Grösse der Bewegung des Cylinders durch (C), und die der Kugel entsprechende durch (K) bezeichnen,
und durch Integration
oder, um es über das ganze Quadrat ACMK zu erstrecken,
Ferner
und
Die Kugel verhält sich zum umschriebenen Cylinder wie
Da nun im I. Satz, Zusatz 6. die Masse des Cylinders durch m bezeichnet wurde, so wird jetzt (nach Gleichung 6.) die Masse der Kugel m' = ⅔m.
Ferner wollen wir die Bewegung des Ringes ACD um seinen Mittelpunkt durch (R) und die Bewegung des Ringes EFKJ um seinen Durchmesser EK durch (R') bezeichnen; alsdann ist nach III. Satz, 4. (R) : (R') = π : 2. Verbinden wir nun die folgenden Proportionen mit einander: (K) : (C) = 3r²π : 4(2r)², (C) : (R) = 2m : 3μ = 3m' : 3μ = m' : μ, (R) : (R') = π : 2; so ergibt sich
oder kürzer (K) : (R') = m' · : μ; (K) : (R') = 925275m' : 1000000μ.
Diese hier aufgeführten Sätze sind im Wesentlichen der Angabe von Newton’s Werken: Isaaci Newtoni Opera quae extant omnia. Commentarius illustrabat Samuel Horsley. L. L. D. R. S. S. Londini MDCCLXXXII. entlehnt. Nur die Führung der Beweise weicht von der dortigen etwas ab. No. 297. S. 458. Im ursprünglichen Texte hat Newton die stündliche mittlere Bewegung der Knoten = 16II 35III 16IV 36V angegeben, deren Hälfte = 8II 17III 38IV 18V den im Text aufgeführten Werth für das siderische Jahr ergibt. Aus dem von mir benutzten abgekürzten, etwas zu grossem Werthe 8,"3 hat sich der in Klammern aufgeführte Werth für das Jahr ergeben.
No. 298. S. 459. Aus 100 : 292369 und 2 : 5, folgt durch Zusammensetzung 10 : 73092.
No. 299. S. 463. Setzt man den Glanz des Kometen und des Planeten G und g, ihren Abstand A und a, ihre Durchmesser D und d; so hat man G : g = , also A : a = .
No. 300. S. 464. Bei diesen Betrachtungen hätte wohl auch erwogen werden müssen, ob die Kometen dieselbe Fähigkeit, das Licht zu reflectiren, wie die Planeten besitzen. Dieser Punkt scheint auch heutigen Tages noch nicht entschieden zu sein.
No. 301. S. 466. Es möge hier daran erinnert werden, dass Encke bei dem nach ihm benannten Kometen von kurzer Umlaufszeit den Widerstand eines Mittels angenommen hat, um eine beschleunigte Rückkehr des Kometen zum Perihel zu erklären. Bis jetzt hat man bei keinem andern Kometen einen ähnlichen Widerstand anzunehmen nöthig gehabt, während, wenn man dies künftig bei mehrern Kometen annehmen müsste, dieser Umstand gegen die im gegenwärtigen Zusatz ausgesprochene Behauptung, dass der Weltraum von jedem widerstandsfähigen Mittel frei sei, sprechen würde.
No. 302. S. 467. Die mittlere tägliche Bewegung der Erde wird t = , d. h. für a = 100000000 t = 1720213 und hieraus stündlich 71675,5. Ferner wird t · = 2432748 und stündlich 101364,5.
No. 303 S. 469. Die hier gefundenen Ausdrücke stimmen offenbar mit denjenigen überein, welche heutigen Tages in der Lehre der Interpolation dargestellt werden. Hiervon kann man sich leicht überzeugen, wenn man hier dieselbe Bezeichnung einführt, welche in der Abhandlung über Interpolation von Encke im astronomischen Jahrbuche für 1830 angenommen ist.
No. 304. S. 470. Setzt man nämlich (Figur im Text) Jμ = a, AJ = JC = b, AJO = α, so ist ACXA = ⅔ 2ab sin α, AEXμA = AJμ + μJEX = ⅔ab sin α + ½(EJ + μX)a sin α oder weil μX JE und μX = ⅓JE, AEXμA = a sin α[⅔b + ½ · 4/3EJ] = ⅔a sin α b + FJ] = ⅔a · AE · sin α und so ACXA : AEXμA = 2b : AE = AC : AE. Indem wie vorhin μX AC und daher Oμ : OJ = 1 : 3.
No. 305. S. 471. Setzt man den Winkel, welchen die im neuen Scheitelpunkte μ, an der Parabel gezogene Tangente mit der Hauptaxe bildet, = α, den Parameter = p, so ist die Gleichung der Parabel, in Bezug auf μ als Scheitel und μJ als Durchmesser, allgemein: x² = x.

Im vorliegenden Falle entspricht μ der, im Brennpunkte S errichteten Ordinate und es ist daher Sμ = SF = ½p, α = 45°, also JC² = JA² = JA · JC = · JM = 2p · JM = 4 · ½p · x = 4 · Sμ · x und der neue Parameter = 4S/μ. Ferner wird, weil α = MJμ = JMμ = 45°, x = Jμ = Mμ = .
No. 306. S. 471. Denken wir uns auf der Tangente gleiche Stücke μμ', μ'μ", etc. μμI, μIμII etc. dies- und jenseits μ abgetragen, und aus jedem der so erhaltenen Punkte Parallelen μ'ν', μ"ν", etc. mit Sμ gezogen, so wird Sμμ' = Sμν', Sμ'μ" = Sν'ν" etc. und so endlich die ganze dreieckige Fläche gleich der parabolischen. Denken wir uns ferner aus C die Ordinate CD gefällt, so wird, weil (Fig. 209.) SAC = 45°, CD = DA = 2 · Sμ = 4AS und SD = 3 · AS; mithin jetzt ASCμA = ⅔AD · DC — ½SD · DC = ⅔ · 4AS · DC — ½ · 3AS · DC; ASCμA = 7/6AS · DC; ASC = ½AS · DC und ASCμA : ASC = 7/3AS : AS = 2 AS + ⅓AS : AS = Sμ + ⅓JM : SM = SN : SM. Setzt man nun den beschriebenen Theil der Tangente = T, so wird T · Sμ : AC · SM = SN : SM und T : AC = SN : Sμ.
No. 307. S. 471. Es ist nämlich SP = = Sμ + ⅔Jμ...
No. 308. S. 472. Setzt man den kleinen Bogen im Kreise = b, Höhe SP = r, die Zeit = t und die der letztem entsprechende Fallhöhe = a; so ist a = t² und eben so die, der Zeit ½t entsprechende Fallhöhe a' = ¼t². Es ist aber b : AC = 1 : , also b² = ½AC², also a' = ¼ · t² = · t² und für t = 1, a' = .
No. 309. S. 478. Es ist an der bezeichneten Stelle X = 8528,4 aufgeführt; da X in dieser Aufgabe nur als ein Punkt aufgeführt ist, muss vielleicht hier XZ statt X gelesen werden.
No. 310. S. 479. Es sei P♌K die Bahn des Kometen, ῶ♌E die Ebene der Ekliptik, ♌ der aufsteigende Knoten, P das Perihel, Pῶ ein Perpendikel von P auf die Ekliptik; alsdann ist P♌ = 8° 38', P♌ῶ
= 61° 20⅓', mithin tang ῶ♌ = tang P♌ · cos P♌ῶ; ῶ♌ = 4° 10'; sin ῶP = sin P♌ · sin P♌ῶ, ῶP = — 7° 34' Länge des Perihels ♈ῶ = ♈♌ — ῶ♌ = 271° 53' — 4° 10' = 267° 43' = ♐ 27° 43'.
No. 311. S. 480. Sind σ und τ die beiden im Text erwähnten Sterne, ist τE parallel der Ekliptik, so hat man, wenn σE auf τE senkrecht ist, σE = 2° 15', τE = 2° 48'5 tang στE = = tang 38° 42' und wenn KM = 10' bis 12', der Unterschied des Kometen und mittlern Punktes M beider Sterne

| Demnach des | Kometen Länge | ♍ | 15° 39,'2 | — 6,'9 | =♍ | 15° 32', |
| Nördliche Breite | 0° 34' | — 8,'6 | = | 0° 25,'4. |
No. 312 S. 481. Nach der Stelle dieses §., welche in der vorhergehenden Bemerkung besprochen worden ist, wurde die beobachtete Breite des Kometen am 10. November gleich 0° 25' 24" im Text anzusetzen und hiernach R . — B . = — 0' 17" sein.
No. 313. S. 482. Irre ich nicht, so müsste hier statt 5h 9m gelesen werden 4h 51m.

No. 314. S. 484. Ist AB die Ekliptik, die durch α Virg. C und α Leon, gehende Linie diejenige gerade Linie, welche die Aehre und das Herz des Löwen verbindet. Alsdann ist die Länge des Punktes A nach dem Texte ♎ 19° 23' 47" = 199° 24', die Breite von α Virg. = — 2° 2', die Länge von C = ♏ 3° 46' = 153° 46', also AC = 45° 38' und wenn man ACα Virg. = x setzt, sin AC · tang x = tang Aα Virg., so wie wenn man die Werthe von AC und Aα Virg. substituirt, x = 2° 51'. Denkt man sich nun den Kometen auf der geraden Linie α Virg. C&alpha Leon. in der Länge ♏ 3° = 213°, so wird seine südliche Breite bestimmt durch sin 59° 14' · tang 2° 51' = tang 2° 27'.
No. 315. S. 484. Nach der im Text vorhergehenden Bemerkung ist die Breite der Spica = — 2° 2'; mithin liegt die Breite des Kometen am 22. November zwischen 2° 2' und 2° 26' und ist im Mittel = — 2° 14'.
No. 316. S. 484. Wie in Bemerkung 314. findet man aus ♏ 12° 52' — ♍ 3° 46' = 222° 52' — 153° 46' = 69° 6'; sin 69° 6' tang 2° 51' = tang 2° 40'; also war hiernach die südliche Breite etwas weniger als 2° 40'. No. 317. S. 487. Nach der Tafel, Pag. 545. war am 12. December die Lange des Kometen ♑ 6° 32' = 276° 32', seine Breite + 8° 29', das obere Ende des Schweifes nach Pag. 551
| in Länge | ♒ 4° | = 304° | |
| „ Breite | + 42° 30', |
| anderweitig | in Länge ♊ 22° | = 352°, |
| „ Breite | = 61°. |
Demnach der Unterschied beider Enden des Schweifes
| in Länge | = 27° 28' | und | 75° 28', |
| „ Breite | = 34° 1' | „ | 52° 31'. |
Hieraus die Länge des Schweifes
oder im Mittel
No. 317. S. 487. Die Dauerhaftigkeit der Kometen ist, nach Newton’s Zeit, durch die Wiederkehr mehrerer derselben direkt erwiesen worden. Dass sie nicht aus gasförmiger Materie bestehen, hat man daraus abgenommen, dass Sterne, welche durch sie hindurch beobachtet worden sind, keine Spur von Strahlenbrechung gezeigt haben. Gegen eine bedeutende Dichtigkeit ihrer Materie spricht der Umstand, dass sie keine Störung auf Planeten, denen sie sehr nahe kommen, ausüben. Schliesslich wollen wir auch bemerken, dass es nach den jüngsten Erfahrungen wahrscheinlich geworden ist, dass die Kometen als ein Aggregat sogenannter Meteoriten (Sternschnuppen) betrachtet werden müssen.
No. 319. S. 488. Unter der Voraussetzung, dass die Materie des Kometen, unter übrigens gleichen Umständen, eben so stark wie unsere Erde im Sommer durch die Sonne erwärmt werden kann; verhält sich die Erwärmung des erstem in seiner Sonnennähe zur Erwärmung der Erde, wie 2806 : 1. Bezeichnen wir die Temperatur des Kometen durch k, die der Erde durch e, die des kochenden Wassers durch w und die des glühenden Eisens durch g; so wird nach den im Text angeführten Werthen k : e = 28600 : 1, e : w = 1 : 3, w : g = 1 : 3(4), also k : g = 28000 : 9(12) = 3100 : 1 = (2300 : 1).
No. 320. S. 488. Die Menge der in einer Kugel eingeschlossenen Materie ist dem Cubus, die Oberfläche dem Quadrat des Durchmessers proportional; die Dauer der Abkühlung wird daher direct dem Cubus und indirect dem Quadrat des Durchmessers, d. h. dem Durchmesser selbst proportional sein. Die Werthe, welche hier in Betracht kommen, sind, wenn sie in gleichen Einheiten ausgedrückt werden: Durchmesser der Kugel 1 Zoll, der Erde = 1728 · 24000 · 12 = 497664000 Zoll = 41473000 Fuss, Dauer der Abkühlung der Kugel 1 Stunde, der Erde = x, also folgt aus 1 Zoll : 497664000 Zoll = 1 Stunde : x Stunden, x = 497664000 Stunden = 20736000 Tagen = 50000 Jahren ungefähr. Hiernach müsste der Text wohl geändert werden, die Resultate stimmen überein.
No. 321. S. 492. Es sei (in der Figur zu §. 30., zweiten Buches) S das Centrum der Erde, SA ihr mittlerer Halbmeseer = 19618800' = r, AC = 850' und daher SB = 19616650' = a, SF = 2r, die Potenz der Hyperbel fah = r²; also Aa = r, Ff = ½r und Bb = ; so wie ferner Aa — Ff = ½r, Aa — Bb = . Es sei die Dichtigkeit AH = St = m = 33, BJ = Sn = n = 32, FZ = SZ = d. Ferner nach der Natur der Hyperbel
und nach Buch II., §. 30., Zusatz
also log log33/32 = 1961665/170 · 0,0183639 = 154,2087935.
Der Halbmesser der Erdbahn ist = 21000000 Meilen, etwa = 500.000.000.000', der Halbmesser der Saturnsbahn zehnmal so gross = 5000.000.000,000', der Durchmesser der Saturnsbahn = 10000.000.000.000' = 120000.000.000.000". Es verhält sich daher die Saturnskugel zu einer Kugel, deren Durchmesser = 1", wie
ein weit kleineres Verhältniss, als das in 3. gefundene Verhältniss der Dichtigkeiten 1617 · 10151 : 1. Daher würde eine Kugel von 1" im Durchmesser unserer Luft bei der Dichtigkeit, welche diese in der Höhe Eines Halbmessers der Erdbahn hat, den ganzen Raum der Planeten bis zum Saturn und jenseits ausfüllen.

No. 322. S. 493. Es stelle S die Sonne, AB einen Theil der Kometenbahn dar. Es sei N der Kern des Kometen, welcher von A gegen B fortschreitet, C das Ende des Schweifes. Zieht man CS, so bezeichnet der Durchschnittspunkt d mit der Bahn den Ort, in welchem der am Ende des Schweifes befindliche Dampf vom Kopfe aufzusteigen begonnen hat, wenn jener Dampf geradlinig von der Sonne aufsteigt. Da diese nicht der Fall ist, sondern der Dampf nach der Seite A, welche der Komet verlassen hat, nach dem Obigen hinneigt; so ziehe man SE parallel der Länge des Kometen, oder vielmehr, wegen der krummlinigen Bewegung des Kometen, von dieser Linie divergirend. Die Linie SE schneide die Bahn in D, und<section end=322 / es wird der, jetzt das Ende des Schweifes bildende, Dampf vom Kern aufzusteigen begonnen haben, als der Komet sich in D befand. Die aufsteigende Bewegung des Dampfes wird nämlich mit der fortschreitenden Bewegung des Kometen zusammengesetzt. Nach den entwickelten Methoden kann man aber die Zeit bestimmen, in welcher der Komet sich im Punkte D befunden hat, und die Zwischenzeit, welche den Oertern D und N des Kometen entspricht, stimmt mit derjenigen überein, welche der Dampf braucht, um vom Kopfe bis zum Ende des Schweifes aufzusteigen.

Es stelle S die Sonne, T die Erde, STA den Winkelabstand des Kometen von der Sonne dar, und es sei ATB die scheinbare Länge des Schweifes. Weil das Licht sich vom Ende des Schweifes längs TB fortpflanzt, so befindet sich das Ende desselben irgendwo auf dieser Linie, etwa in D. Man ziehe DS, welche AT in C schneidet; alsdann werden, weil der Schweif immer sehr nahe der Sonne gegenüberliegt, die Sonne, der Kopf und der Endpunkt des Schweifes in gerader Linie, der zweite also in C liegen. Zieht man SA TB, so liegt C zwischen T und A, weil das Ende des Schweifes irgendwo auf der unendlichen Linie TB liegt und alle Linien, welche von S nach TB gezogen werden können, TA irgendwo zwischen T und A schneiden. Der Komet kann daher von der Erde nicht weiter als TA und von der Sonne nicht Leiter als SA entfernt sein.
Z. B. der Komet von 1680 hatte am 12. December die Länge 276° 32', die Breite 8° 28', die Sonne die Länge 271° 51' (nach Pag. 538.) Unterschied der Längen = 4° 41'; mithin der Abstand des Kopfes von der Sonne aus cos KS = cos 4° 41' · cos 8° 28', KS = 9° 40' = ATS. Die Länge des Schweifes, oder ATB = 35°, SA : ST = sin 9° 40' : sin 35° = 3 : 10. Der Komet war daher an diesem Tage von der Sonne nur am 3/10 r entfernt, wo r der mittlere Abstand der Erde von der Sonne bezeichnet. Jener befand sich also innerhalb der Mercursbahn.
Am 21. December war Länge des Kometen 305° 8', Breite = 21° 42', Länge ☉ 281° 7', mithin cos KS = cos 24° 1' · cos 21° 42', KS = 31° 56' = ATS, ATB = 70°, SA : ST = sin 31° 56' : sin 70° = 4 : 7. Der Komet war noch innerhalb der Venusbahn.
Am 28. December war Länge des Kometen 338° 41', Breite 28° 6', Länge ☉ 288° 26', cos KS = cos 50° 15' · cos 28° 6', KS = 55° 40', Länge des Schweifes = 56°, SA : ST = sin 55° 40' : sin 56°. Der Komet befand sich also noch innerhalb der Erdbahn. No. 323. S. 495. Ich kann der hier aufgestellten Schlussfolge nicht ganz beistimmen.
Ich glaube nämlich nicht, dass von der Feuchtigkeit; womit unsere Erde ausgestattet ist, ihr beim Process des Wachsens und Faulwerdens der Pflanzen etwas verloren gehe, sondern dass die hierzu erforderliche Feuchtigkeit nur von andern Theilen der Erde hergeliehen, und dass dieselbe bei eintretender Fäulniss durch Verdunstung wieder frei und zu anderweitigen Operationen verwendet werde. Nur dann erst könnte ich in Bezug auf die Erde der Schlussfolgerung im Texte beitreten, wenn zuvor nachgewiesen wäre, dass bei den beiden Operationen die absolute Menge des Flüssigen vermindert und die des Festen vermehrt werde. Denselben Haushalt stelle ich mir auf den Planeten vor, so dass auch diese keiner äussern Zuführung von Flüssigkeit bedürfen. Ist endlich die bisher besprochene Hypothese, dass durch die Wärme der Sonne aus den Kometenköpfen entwickelten Dämpfe die Schweife gebildet werden, begründet; so ist es am einfachsten anzunehmen, dass diese Dämpfe, bei der Entfernung der Kometen von der Sonne, niedergeschlagen werden und zu den Köpfen zurückkehren.
Sollte übrigens die bereits erwähnte Meinung, wonach eine gewisse Identität zwischen den Kometen und den Meteorsteinen besteht, sich bestätigen; so würde man Veranlassung haben, neue und wesentlich andere Hypothesen über das Wesen und die Entstehung der Schweife aufzustellen.
No. 324. S. 487. Die Praemisse dieses Satzes wird durch die neu entdeckten kleinen Planeten (die Asteroiden) wesentlich modificirt, da sie entschieden kleiner sind, als die vier der Sonne näher gelegenen Planeten.
No. 325. S. 499. Es sind der Reihe nach
| die | Flächenränme | D und E, | d und e, | δ und ε, |
| „ | Zwischenzeiten | A „ B | ||
| „ | ganzen Zeiten zwischen 1. und 3. Beobachtung | T | t | T |
| „ | ganze richtige Zwischenzeit | S | ||
| „ | Knotenlänge | K | K + P | K |
| „ | Neigung | J | J | J + Q. |
Wären die Flächenräume den Zeiten entsprechend, so müssten sie einander proportional sein, und wir hätten
da dies nicht der Fall, setzen wir wie im Texte
| 2. | A : B = C : 1 D : E = G : 1 d : e = g : 1 δ : ε = γ : 1 |
und wir erhalten alsdann folgende Proportionen und Gleichungen:
| 3. | T — τ | : T — S | = Q : x |
| G — γ | : G — C | = Q : y | |
| T — t | : T — S | = P : x' | |
| G — g | : G — C | = P : y' |
also
Damit nun so wohl x und y, als x' und y' einander gleich werden, setzen wir , = m, erhalten hieraus T — S = n(T — τ); G — C = n(G — γ), T — S = m(T — t); G — C = m(G — g) und so die Bedingungsgleichungen:
| 8. | 2T — 2S = m(T — t) + n(T — τ) 2G — 2C = m(G — g) + n(G — γ), |
welche zur Bestimmung von m und n dienen. Mittelst dieser so gefundenen Werthe erhält man dann nach 4.—7. die Werthe des Knotens und der Neigung bezüglich K + mP und J + nQ.

No. 326. S. 501. Der Inhalt dieses Abschnittes ist mir nicht klar. Stellen γ, A, K die bezüglichen Oerter von Stern γ, A und Komet dar, so erhält man aus den Breiten von γ = + 7° 8' 58", A = + 8° 28' 33" und dem Längenunterschiede = 0° 6' 0", den Abstand Aγ = 1° 19' 48"'. Ist nun Gγ der Breiten parallel von γ, AG darauf senkrecht, so folgt aus AG = 1° 19' 35", Aγ = 1° 19' 48", der Winkel AγG = x aus sin x = ; nämlich x = 85° 46' 39", und daher, weil AγK = 90°, Kγg = y = 4° 13' 21", so wie gγ und gK, welche letztere auf Gγ normal, weil Kγ = Aγ, gγ = 1° 19' 35" und da die Länge von γ = ♈ 28° 30' 15", gγ sec. 7° 8' 58" = 1° 20' 12", die Länge von K = ♈ 27° 10' 3", gK = 0° 5' 53" und die Breite des Kometen K = 7° 8' 58" — 0° 5' 53" = 7° 3' 5". Diese Werthe der Länge und Länge und Breite des Kometen stimmen nicht mit den in der vorhergehenden Tabelle für Febr. 7 gegebenen überein.
No. 327. S. 505. Bekanntlich ist dieser Komet, der Halley’sche, so wohl 1759 als 1835, den angestellten Rechnungen entsprechend, wiedergekehrt.
No. 328. S. 505. Hiervon machen die verschiedenen, in der neuern Zeit entdeckten und berechneten Kometen von kurzer Umlaufszeit eine entschiedene Ausnahme. No. 329. S. 506. In Bezug auf diese Stelle im Texte möge nur kurz bemerkt werden, dass bis jetzt bei den Berechnungen der Kometenbahnen die Störungen gehörig berechnet worden sind, welche sie von Seiten der Planeten erleiden. Dagegen hat sich noch keine Veranlassung gezeigt, auch auf etwaige Störungen, welche die Kometen ausüben, Rücksicht zu nehmen. Man betrachtet ihre Masse als verschwindend klein.
No. 330. S. 507. Die Grenzen des Zodiakus haben bekanntlich auch in der neuern Zeit für die kleinen Planeten erweitert werden müssen.
No. 331. S. 507. Vergleiche vorstehende Bemerkung 329.
No. 332. S. 508. Die ungeheuren Abstände, in denen sich die Fixsterne von einander befinden, würden allein ihr Zusammenfallen vermöge der allgemeinen Gravitation nicht verhindern können. Man muss vielmehr annehmen, dass dieses eben so verhindert wird, wie das Zusammenfallen der Planeten mit ihrem Centralkörper, der Trabanten mit ihrem Planeten, durch eine den Fixsternen eigenthümliche fortschreitende Bewegung, welche mit jener allgemeinen Anziehung im Gleichgewichte steht. Eine derartige eigene Bewegung wird aber um so wahrscheinlicher, als die Zahl der Fixsterne fortwährend wächst, bei denen man eine eigene Bewegung wahrnimmt und ein Theil der letztern durch die Annahme der Bewegung unseres ganzen Sonnensystemes nach einem bestimmten Punkte des Himmels erklärt wird. Gar leicht und einfach schliesst man aus diesen Betrachtungen, dass im gesammten erkennbaren Weltraume keine absolute Ruhe, sondern beständige Bewegung stattfinde.
No. 333. S. 511. In den auf Newton folgenden Zeiten ist die Grenze der Wirksamkeit der Schwere thatsächlich über den Saturn hinaus erweitert werden. Nicht nur der später entdeckte Planet Uranus und der Halley’sche Komet bewegen sich, den in diesem Werke entwickelten Gesetzen der Schwere entsprechend; sondern es wurde ja auch vor etwa 30 Jahren, in Folge der vervollkommneten Theorie, Leverrier und Adams möglich, aus den Störungen, welche Uranus in seinem Laufe erlitt, auf die Ursache derselben, den weiter entfernten Planeten Neptun und seinen. Ort zu schliessen.
No. 334. S. 513. Ich bitte, hier die vorhergehende Bemerkung 332. zu beachten.
No. 335. S. 521. Setzt man die Masse der Erde = T, die des Mondes = L, so soll die Reihe T + L, (T + L)x, (T + L)x², (T + L)x³ dergestalt gebildet werden, dass (T + L)x³ = T, also x = werde. Das im Texte erwähnte erste Glied ist aberund das Verhältniss T + L : .
| Für | den mittlern scheinbaren Durchmesser | des Mondes | = 31,'5, |
| und für | „ „ „ „ | der Erde | = 114,6, |
wird T : L = (114,6)³ : (31,5)³ = 42 : 1

No. 336. S. 522. Setzt man den mittlern Abstand der Erde von der Sonne = 10000; so ist der mittlere Abstand des Jupiters von der Sonne, oder SJ = 52012 und der mittlere Abstand der Venus von der Sonne = 7234. Wenn nun die grösste Elongation des 4. Trabanten, oder TSJ = 8' 13" und der wirkliche Abstand JT = x gesetzt wird; so hat man x = SJ tang 8' 13" = 124 und so x : SJ = 124 : 52012 und ähnlich x : SV = 124 : 7234, wo SV den mittlern Abstand der Venus von der Sonne bezeichnet.
No. 337. S. 522. Es wird, weil 16d 18h = 402h, 224d 16h = 5392h, das gesuchte Verhältniss = 767 : 249 = 442 : 143. Ferner 442 · = 0,13 und 0,13 : 143 = 1 : 1100.

No. 338. S. 524. Für CF = 191382, FG = 3, wird FCG = 3/191383 206265" = 3,"25 und nicht = 3,"14 wie im Text.
No. 339. S. 525. Der Durchmesser des Jupiters wird, nach den im Text angegebenen Werthen, = = 39,"6.
No. 340. S. 527. Es ist in der neuern Zeit wohl von sympathetischen Pendeln, d. h. solchen die Rede gewesen, welche bei gleicher Form und Länge neben einander schwingend, bald gleichförmig zu schwingen anfangen. Hieraus könnte man einen Einwurf gegen die im Texte von Newton beschriebenen Versuche und die Strenge der daraus gezogenen Schlüsse abnehmen.
Dieser Einwand wird bei den neuern Versuchen von Bessel fortfallen, wo die Schwingungen der Pendel bei verschiedenen Substanzen, jede für sich beobachtet wurden.
No. 341. S. 529. In der spätern Zeit hat man die Ablenkung des Lothes von der vertikalen Richtung beachtet und zu bestimmen versucht. Es möge hier an den Berg Shehallien erinnert werden.
No. 342. S. 531. Für die Umlaufszeit
| der Venus | = 224,d7 | finde ich ihre Fallzeit | = | 39,d72, |
| des Jupiters | = 4332,58 | „ „ „ „ | = 2 Jahre | 35,d4, |
| der Erde | = 365,26 | „ „ „ „ | = | 64,d569. |
No. 343. S. 532. Vergleiche die frühere Bemerkung 332.
No. 344. S. 532. Dieser letzte Satz wird gegenwärtig wesentlich modificirt durch die beiden später entdeckten und weiter entfernten Planeten Uranus und Neptun, wogegen die vielen Asteroiden, in Folge ihrer verschwindend kleinen Masse, als wirkungslos in dieser Beziehung betrachtet werden können.
No. 345. S. 534. Der Inhalt dieses §., namentlich des letzten Satzes ist höchst interessant, indem Newton aus den vorher auseinander gesetzten Bewegungen mit grosser Wahrscheinlichkeit auf das Vorhandensein des damals noch unbekannten Planeten Uranus schloss. Nur dieser, nicht aber die ganz oder fast ganz masselosen Kometen konnten als Ursache der wahrgenommenen Aenderungen in den Elementen der bekannten Planeten in Betracht kommen.
Nachdem etwa ein Jahrhundert später der Uranus durch Zufall entdeckt worden und seine lange genug verfolgten Bewegungen ähnliche Störungen gezeigt hatten, haben Leverrier und Adams aus diesen nicht allein das Vorhandensein eines weitem äussern Planeten als wahrscheinlich abgeleitet, sondern auch den Ort desselben, des Neptuns, so nahe richtig vorher angezeigt, dass derselbe sogleich aufgefunden werden musste.
No. 346. S. 535. Da allgemein das Differential der Fläche des vom Monde beschriebenen Sectors = ½r²dv und hier dasselbe proportional der Summe 237,3 + sin vers.: so wird r² = , wo a eine Constante bezeichnet.
No. 347. S. 536. Die Umlaufszeit des vierten Trabanten ist
| =16d 16h 32m | = ♃☽, | ||
| unseres Mondes | = 27,d32166 | = ♁☾. | |
| Die sider. Umlaufszeit | des Jupiters | = 4332,d5848 | = ♃, |
| „ „ „ | der Erde | = 365,d25637 | = ♁. |
Die 100jährige rückläufige Bewegung des Mondknotens = 5 Umläufe 134° 9' 57,"5 = 18134° 10' = Δ♌, mithin die 100jährige Bewegung des Knotens des vierten Trabanten
| = Δ♌' : Δ♌ = | ♁² : ♃² ♃☾ : ♁☾ |
und mittelst der vorstehenden Werthe, welche nach Hansen a. a. O. angesetzt sind, Δ♌' = 8° 24'. Ko. 348. S. 512. Vermuthlich muss hier 18. statt 13. gelesen werden.

No. 319. S. 545. Der grösste Unterschied der Fluthhöhe wird offenbar in den Punkten A und B stattfinden, weil CA der grösste und CB der kleinste Halbmesser und daher
ein Maximum ist.
Weil CE = CF > CB, wird
also zwischen der Mitte A und den Küsten E und F des EF breiten Meeres ein geringerer Unterschied der Fluthhöhe, als zwischen A und B stattfinden. Ferner wird
und daher zwischen den Küsten E und F des EF breiten Meeres gar kein Unterschied in der Fluthhöhe stattfinden.
Betrachten wir das ef breite Meer, so ist Ce nahe dem grössten Werthe CA, Cf nahe dem kleinsten Werthe CB gleich und da CD < CA und CD > CB; offenbar
Der Höhenunterschied der Fluth zwischen der Mitte D und den Kästen e und f des ef breiten Meeres ist geringer als der zwischen e und f selbst. Man ersieht hieraus zugleich, dass der letzte Unterschied desto grösser ist, je grösser die Breite ef des betreffenden Meeres vorausgesetzt wird. Hierbei muss aber der Winkel eCf am Mittelpunkte C der Erde kleiner als 90° sein, weil ein rechts von CB liegender Halbmesser Cf grösser als der letztere und daher Ce — Cf wieder kleiner werden würde.
No. 350. S. 547. Setzt man nämlich die bestimmte Höhe, für welche man das Gewicht bestimmen will, = h, eine unbestimmte Höhe = x und bezeichnet c eine Constante; so erhält man das Gewicht für die Höhe h aus cxdx = ½ch².
No. 351. S. 547. Vergleiche §. 41. des dritten Buches.
No. 352. S. 548. Genauer folgt hier 5L + 5S = 15165/2000 L — 9S, L = 28000/5165 S = 5218/518 = 53/5.
No. 353. S. 548.
| Es ist in den Syzygien | = 1685/2000, T = 1685/2000, |
| „ „ Quadraturen | = 2000/2000, T = 1685/2000, |
also 1685/2000 L + 1685/2000 S : L — 1685/2000 S = 6 : 5, woraus L = 566/358S = 51/5S und im Mittel L = 53/10S = 5⅓ S, so wie L + S = 6⅓ S folgt.
No. 354. S. 549. Aus ergiebt sich der Werth 2031821, welcher von dem im Texte aufgeführten Werthe zwar verschieden ist, aber so wenig, dass der dort gezogene weitere Schluss richtig bleibt.
No. 355. S. 550. Nach der 4. Erscheinung des dritten Buches beträgt der mittlere Abstand des Saturns von der Sonne etwa 950000, wenn der mittlere Abstand der Erde von der Sonne = 100000 gesetzt wird; also die jährliche Parallaxe des Saturns = 100000/950000 ·3437,'7 .... = 361,'8. Da nun die jährliche Parallaxe der Fixsterne < 1'; so müssen diese mehr als 360 mal weiter von der Erde entfernt sein, als der Saturn.
No. 356. S. 551. Der ganze Inhalt dieses §. ist wohl mehr von theoretischem, als praktischem Interesse; auch scheinen mir die darin enthaltenen Zahlenangaben nicht ganz richtig. Deshalb einige Bemerkungen. Nehmen wir den Abstand der Erde von der Sonne S = 10000, den Abstand des Saturns von der Sonne K = 95388, den Abstand des Fixsterns = x; so ist nach dem Text < 1' oder x · 1' > 10000, d. h. > 10000, oder x > 34377466, und da 360 · R = 34339680, x > 360 · R. Der scheinbare Durchmesser des Saturns ist = 17,"1, mithin sein wirklicher Durchmesser D = 2 · 95388 sin 8,"55 und daher sein wirklicher Halbmesser r = 95388 sin 8,"55,
| log 95388 | 4,97048 |
| „ sin 8,55 | 5,61754 |
| log r | 0,59702 |
Die Fläche der Saturnsscheibe ist = r²π, die Fläche der Kugel zur mittleren Entfernung des Saturns von der ☉ = 4R²π mithin ihr gegenseitiges Verhältniss r² : 4R² = [1,19404] : [10,56102] = 1 : 2300000000, wofür im Text 1 : 2100000000. Die in den Klammern enthaltenen Zahlen bezeichnen Logarithmen.
Setzt man den wirklichen Durchmesser der Erde = 1, so ist die mittlere Entfernung der Erde von der Sonne D = 12027 und der wirkliche Durchmesser der Sonne Δ = 112,06. Es wird daher der scheinbare Halbmesser der Sonne = · 206264,"8 = 16' 0,"9, ihr Durchmesser = 32' 1,"8. Ferner die Parallaxe der Sonne = 206264'8 = 8,"5752. Die Sonne soll sich nun in der Entfernung 100000 · 9,53885 = 953885 von der Erde befinden, und da für d = 1 und Δ = 112,06, D = 12027 ist, so wird, wenn wir den 953885 entsprechenden Werth durch D' bezeichnen, aus 1 : 12027 = 953885 : D', also D' = 11472674895. Nach dem Texte sollte nun, wenn 206264,"8 = ω gesetzt wird.Ich erhalte D' für den ersten Werth 7IV 17V und für den zweiten 13III.
Aus dem im Eingange dieser Bemerkung angegebenen Grunde enthalte ich mich weiterer Ausführung.
No. 357. S. 562. Nach §. 30., Zusatz des zweiten Buches haben wir thnz : thkw = Aa — Ff : Aa — Cc oder

Nach der Lehre von der Hyperbel wird aber
| 2. | thnz = log St — log Sz thkw = log St — log Sw |
und nach derselben Lehre SF · Ff = SA · Aa oder
und ebenso |
3. |
Nach den Gleichungen 1. bis 3. wird, wenn man
| St = AH, | d. h. die Dichtigkeit in | A durch | δ0 |
| Sz = FN | „ „ „ | F „ | δ |
| Sw = CK | „ „ „ | C „ | δ1 |
bezeichnet, oder, weil SF — SA = AF und SC — SA = AC, wenn man den Abstand AF = x, AC = a, SC = SA + AC = r + a, SF = SA + AF = r + x setzt, wo r = 4000 englische Meilen den Halbmesser der Erde bezeichnet
und indem man von den Logarithmen auf Zahlen übergeht:
Nach dem Text ist δ0 = 33; a = 1200; δ1 = 32 engl. Fuss, r = 4000 Meilen = 19191600 Fuss, und x der Reihe nach in Meilen = 5, 10, 20, 40, 400, 4000, 40000, 400000, 4000000, ∼. Setzen wir log = log = 0,0133639 = C so folgt aus 5.
und hiernach, folgende tabellarische Rechnung:
| log 33 — | |||||||
| 5 10 20 40 400 4000 40000 400000 4000000 ∼ |
801 401 201 101 11 2 1,1 1,01 1,001 1 |
2,9036325 2,6031444 2,3031961 2,0043214 1,0413927 0,3010300 0,0413927 0,0043214 0,0004341 0,0000000 |
9,4262480 9,7267361 0,0266844 0,3255591 1,2884878 2,0288505 2,2884878 2,3255591 2,3294464 2,3298805 |
0,266842 0,533011 1,06337 2,11621 19,43067 106,86869 194,30673 211,62117 213,62384 213,73739 |
1,2516759 0,9855030 0,4551769 9,4023019 0,XVII08784 0,CV64982 0,CXCII21178 0,CCX89734 0,CCXII99467 0,CCXII78112 |
17,8516 9,6717 2,8521 0,2525 0,XVII1224 0,CV4465 0,CXCII1628 0,CCX7895 0,CCXII9878 0,CCXII6041 |
1,8486 3,4120 11,5701 130,68 26957XV 73908CII 20259CLXXXX 41799CCVII 33414CCIX 54625CCIX |
Diese Darstellung verdanke ich meinem mathematischen Freunde Dr. Tietjen, wonach die Werthe δ bis auf den x = 400000 entsprechenden übereinstimmen. Hier steht im Original 7859 statt 7895, ein oft vorkommendes Versehen. Unser Werth scheint der richtigere zu sein, indem der aus sich ergebende Werth von A hiermit 41799 wie im Original wird. Auch die Werthe von A stimmen nicht alle mit den im Original aufgeführten.
Es ist zwar r = 4000 e. Meilen angegeben, aber nicht wie viele Fuss auf 1 e. Meile gehen, was doch erforderlich, weil a in Fussen ausgedrückt ist. Der Werth von ist demnach aus einen der einzelnen Fälle abgeleitet worden, und zwar am einfachsten aus x = ∼ entsprechenden, wo einfach nach Gl. 6. 1 + also weil hier δ = 0,CCXII6041, log 33 = 1,5185139, log δ = 0,CCXII78112,
log C = log [0,0133639] = 8,1259332 — 10,1 + = 15993,64; = 15992,64, 1 e. Meile = 4797,79 e. Fuss wird.
No. 358. S. 563, Der Saturn ist von der Sonne im Mittel entfernt 197VI g. Meilen = 56736IX Zoll und die letzte Zahl ist weit kleiner, als 73907CII.
No. 359. S. 565. Die halbe grosse Axe der Mercursbahn ist = 0,387, wenn die der Erde = 1 gesetzt wird; mithin ihr Verhältniss = 387 : 1000 oder 4,2 : 11 > 3 : 11.
No. 360. S. 566. Für die Venus haben wir das ähnliche Verhältniss = 723 : 1000 = 5 : 7 > 4 : 7.
No. 361. S. 567. Wir müssen bemerken, dass sich für neuere Kometen die Neigung weit grösser ergeben hat, und daher ihre Breite grösser als 40° werden kann. Ferner sind die Grenzen der Zone, innerhalb deren die Planeten sich bewegen, des sogenannten Zodiacus durch die Entdeckungen der kleinen Planten wesentlich erweitert worden.
No. 362. S. 568. Sind die Tageszeiten Jan. 4. 6h Morgens und Nov. 10. 12h so gerechnet, wie es früher zu geschehen pflegte, dass nämlich der Anfang des Tages um Mitternacht angenommen wurde; so ist Jan. 4, 6h Morgens = Jan. 3. 18h, nach der neuern Anfangszeit des Tages um Mittag,
| Jan. 3. 18h + 16h | = Jan. 4. 10h, d. h. Jan. 4 10h Abds. |
| Nov. 10. 12h Abends | = Nov. 10. 12h und |
| Nov. 10. 12h — 16h | = Nov. 9. 20h = Nov. 10. 8h Morgens nicht 6h wie im Text. |
No. 363. S. 568. Es ist Jan. 4.10h — Dec. 7 = Dec. 35,4 — Dec. 7 = 28,d4, Dec. 7. — Nov. 10,3 = Nov. 37 — Nov. 10,3 = 26,7. Jan. 4. 10h — Dec. 8 = 27,d4, Dec. 8. — Nov. 10,3 = 27,7.
No. 364. S. 569. Nach §. 75. war am 10. Nov. die scheinbare tägliche Bewegung des Kometen = 4⅔°, welcher nach der vierten Columne der Tab. II. der Abstand 347 + · 69 = 360 entspricht.

No. 365. S. 559. Zur Veranschaulichung dieser Stelle im Text sei die Parabel der Bahn dargestellt mit den drei Oertern vom 10. Nov., 8. Dec. und 4 Jan., und dem Punkte S, wo die Sonne sich im Brennpunkte befindet. Die Zeit 27d 16h 4m ist nach Tab. I. 27 16 7, der Unterschied nicht von Belang.
No. 366. S. 570. Aus dem Winkel von 23° folgt
Den letztern Werthe entsprechen nach Tabelle I. nicht 34d wie im Text, sondern 37d.
Diese Tabelle ist offenbar die modificirte Barker’sche Tafel, mittelst welcher die mittlere Bewegung aus der wahren Anomalie gefunden wird. Diese Tafel ist in dem Werke von Olbers: „Abhandlung über die leichteste und bequemste Methode, die Bahn eines Kometen aus einigen Beobachtungen zu finden. Weimar 1797", wie auch in der zweiten, von Encke besorgten Ausgabe. Weimar 1847. enthalten.
Nach derselben fallen die im Texte enthaltenen Zahlenwerthe etwas verschieden aus, jedoch sind die Unterschiede nicht von Bedeutung; da nach des Verfassers Bemerkung die ganze Berechnung in diesem Paragraphen nur eine genäherte sein soll.
No. 367. S. 570. Dem Abstande von 122 Theilen entsprachen in Tab. I. 31½, nicht 30 Tage wie im Text.
No. 368. S. 570. Dem Abstande von 350 Theilen entsprechen 37,2, nicht 33½ Tage, und der erstere Unterschied kommt dem Sept. 16 — Aug. 11 = 36 Tage näher.
No. 369. S. 572. Da SP = , so wird verbessert SP = , ferner SP = , also verbessert SP = . Hier steht im Original fälschlich + e. Es wird hierauf = (SP²)½ + ½ (SP²)-½ BP · e + ½(SP²)-½e² — 1/8(SP²)-3/2 4BP²e etc. = SP + e + ½ e² etc = SP + e + e² etc.No. 370. S. 575. Das Verhältniss , ist identisch mit dem SP : , und dieses geht, wenn es erlaubt ist, statt des geometrischen Mittels das arithmetische zu setzen, über in 2 SP : SP + Sp.
Anmerkungen (Wikisource)
Bearbeiten
| ← Ueber das Weltsystem. | Nach oben |
| Dieser Text wurde anhand der angegebenen Quelle einmal Korrektur gelesen. Die Schreibweise sollte dem Originaltext folgen. Es ist noch ein weiterer Korrekturdurchgang nötig. |






















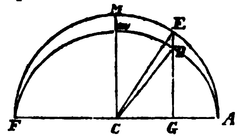


















































![{\displaystyle \scriptstyle \Delta E'={\frac {{\frac {1}{e}}[M-E'+e''\sin \ E']}{{\frac {1}{e}}\mp \cos \ E'}}={\frac {M-E'+e''\sin \ E'}{1\mp e\ \cos \ E'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c1a8b1f67d14d91b271d3dcc1aea1809f3ac7f)






























![{\displaystyle \scriptstyle {\frac {AL\cdot LB\cdot JS}{2}}\int \limits _{LA}^{LB}{\frac {dx}{x^{2}}}={\frac {AL\cdot LB\cdot JS}{2}}\left[-{\frac {1}{LB}}-\left(-{\frac {1}{LA}}\right)\right]={\frac {AL\cdot LB\cdot JS}{2\cdot AL}}-{\frac {AL\cdot LB\cdot JS}{2\cdot LB}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8845bea2e7b3f004dc71e52e730bf7ef5fb22e)
![{\displaystyle \scriptstyle {\frac {LS\cdot JS^{\frac {3}{2}}}{\sqrt {2}}}\int \limits _{LA}^{LB}{\frac {dx}{x^{\frac {3}{2}}}}={\frac {LS\cdot JS^{\frac {3}{2}}}{\sqrt {2}}}\left[-2\cdot LB^{-{\frac {1}{2}}}+2\cdot LA^{-{\frac {1}{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d81bc6aa089d21c0bdbb29a23fd6e3f22845def5)
![{\displaystyle \scriptstyle =LS\cdot JS^{\frac {3}{2}}{\sqrt {2}}\left[{\frac {1}{LA^{\frac {1}{2}}}}-{\frac {1}{LB^{\frac {1}{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24c130adadbc887668900e354a05438e3de9ce70)
![{\displaystyle \scriptstyle {\frac {JS^{\frac {3}{2}}}{2{\sqrt {2}}}}\int \limits _{LA}^{LB}{\frac {dx}{x^{\frac {1}{2}}}}={\frac {JS^{\frac {3}{2}}}{2{\sqrt {2}}}}2\left[LB^{\frac {1}{2}}-LA^{\frac {1}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c905929f852231e4d9e9547b4499df01bc6e9ed1)


![{\displaystyle \scriptstyle ={\frac {LA\cdot LB\cdot JS^{\frac {3}{2}}}{2{\sqrt {2}}}}\cdot {\frac {2}{3}}\left[{\frac {1}{LA^{\frac {3}{2}}}}-{\frac {1}{LB^{\frac {3}{2}}}}\right]={\frac {LA\cdot LB\cdot JS^{\frac {3}{2}}}{3{\sqrt {2}}}}\left[{\frac {1}{LA^{\frac {3}{2}}}}-{\frac {1}{LB^{\frac {3}{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/359411a6a48710ce3cd1f0c8b984ae9f93e07c00)




![{\displaystyle \scriptstyle SJ^{\frac {3}{2}}\cdot {\frac {\left[6LS+3LA-LB\right]{\sqrt {LB}}-\left[6LS+3LB-LA\right]{\sqrt {LA}}}{3{\sqrt {2}}{\sqrt {LA\cdot LB}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f6da1e85821098b3ea7bc2c957786874ec4710d)














![{\displaystyle \scriptstyle \int \limits _{AP}^{PH}ydx=\int \limits _{PA}^{PH}{\frac {dx}{x^{n}}}={\frac {1}{n-1}}\left[{\frac {1}{PA^{n-1}}}-{\frac {1}{PH^{n-1}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b503327fbae18d0cc7d523f9afbfcef4fa2c0d68)
















![{\displaystyle \scriptstyle 2b+{\frac {b}{a^{2}-b^{2}}}\left[b(\alpha +2b)-b\alpha \right]-{\frac {b\cdot 2a^{2}(\alpha +b)}{2\left(a^{2}-b^{2}\right)}}\int \limits _{\alpha }^{\alpha +2b}{\frac {dx}{bz}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d46ffe4cf190b07f93493719698412313049c0a)

![{\displaystyle \scriptstyle \left.-{\frac {2\left[2a^{2}(\alpha +b)-2\left(a^{2}-b^{2}\right)3\right]bz}{4a^{2}\alpha (\alpha +2b)\left(a^{2}-b^{2}\right)-4a^{4}(\alpha +b)^{2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ef47621d7ed9c7ff17600706951a1c7ee3aab1c)

![{\displaystyle \scriptstyle \times \left\{\left[a^{2}(\alpha +b)-\left(a^{2}-b^{2}\right)(\alpha +2b\right]\left(b^{2}+2b\alpha \right)-\left[a^{2}(\alpha +b)-\left(a^{2}-b^{2}\right)\alpha \right]b\alpha \right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8771a593df57f48590a041a7c0059ad13e3a4d9)









![{\displaystyle \scriptstyle \int \limits _{\alpha }^{\alpha +2b}\left(1-{\frac {x}{z}}\right)dx=2b-{\frac {2}{3\cdot 4\cdot (\alpha +b)^{2}}}[2(\alpha +b)x+2\alpha (\alpha +2b)]z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e536cb2007ce8ab68f9a9c3921e1229c59fd76d6)
-\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4517386049dcd29901e6e16779a9d22c374eee47)
![{\displaystyle \scriptstyle \left.[(\alpha +b)\alpha +a(\alpha +2b)]\alpha \right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85a8040d2dc6f48f3d6074767594d7e8fe4b704c)
























































![{\displaystyle \scriptstyle +{\frac {2\cdot MJ\cdot NJ}{HJ}}={\frac {2\left[Q\xi +R\xi ^{2}+S\xi ^{3}\dots \right]\cdot \left[R\xi ^{2}+S\xi ^{2}\dots \right]}{\xi {\sqrt {1+Q^{2}}}+{\frac {QR\xi ^{2}}{\sqrt {1+Q^{2}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/880ac6a08da19e17da6d58cbd477fa57191a6e12)


























![{\displaystyle \scriptstyle {\frac {1}{2}}\left[{\frac {1}{AH}}+{\frac {1}{GT}}\right]={\frac {{\frac {1}{2}}[AH+GT]}{AH\cdot GT}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4811fccfb4838139b4e0ced9ef1512f9a4bf6827)







![{\displaystyle \scriptstyle SQ+VQ-\left[SQ+{\frac {1}{2}}{\frac {SQ\cdot VQ}{SQ}}-{\frac {1}{8}}{\frac {SQ^{2}\cdot VQ^{2}}{SQ^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a99a860a3bb788f401f8689976444792a1a8d760)





![{\displaystyle \scriptstyle AS^{\frac {3}{2}}\left[1+{\frac {1}{q}}+{\frac {1}{q^{2}}}+{\frac {1}{q^{3}}}+\dots \ in\ inf.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89953883f039da22cc3c8b96594a3502d526035e)





















































































![{\displaystyle \scriptstyle \left[{\frac {CO^{2}}{CS^{2}}}(CEB-FG)+FG\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56e594cd3a1b827a65e9fe3aa61cc3fd876df7e3)

![{\displaystyle \scriptstyle \left[{\frac {b^{2}}{b^{2}+(a+x)^{2}}}\left(1-{\frac {x^{2}}{(a+x)^{2}}}\right)+{\frac {x^{2}}{(a+x)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45eb72de6fd3ac6ab5b816d40d49ed349d6bc52b)

![{\displaystyle \scriptstyle {\frac {2b^{2}a\left[ax+x^{2}-b^{2}\right]}{\left[b^{2}+(a+x)^{2}\right]^{2}}}={\frac {Z}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aada27fc890f8745f4e4766481cc27a99af2d50)

![{\displaystyle \scriptstyle {\frac {dZ}{N}}={\frac {2b^{2}a(a+2x)}{\left[b^{2}+(a+x)^{2}\right]^{2}}}={\frac {4b^{2}a{\sqrt {{\frac {1}{4}}a^{2}+b^{2}}}}{\left[b^{2}+\left({\frac {1}{2}}a+{\sqrt {{\frac {1}{4}}a^{2}+b^{2}}}\right)^{2}\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40278b5ef6556fde48056d206ba6d2a1cd59f71c)






























![{\displaystyle \scriptstyle \log \left[{\frac {(N+1)^{2}}{4N}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24131e60584f1d02815b3f48d2e2c408124d4b64)

![{\displaystyle \scriptstyle \log \left[{\frac {(N+1)^{2}}{4N}}\right]={\frac {2PF}{G}}\log \left[{\frac {(N+1)^{2}N}{4N^{2}}}\right]={\frac {2PF}{G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd185747821081c51066dd761d24452aeba95e9d)





![{\displaystyle \scriptstyle {\sqrt[{3}]{79{\frac {13}{38}}:132,8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03e170cd3d1e1e098064b4a1d26c029aec9557a6)

























![{\displaystyle \scriptstyle {\sqrt[{3}]{S+P}}:{\sqrt[{3}]{S}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1dca3a0d6b4262c1d662f237ff045e64eab80e6)
![{\displaystyle \scriptstyle a{\sqrt[{3}]{\frac {88,75}{87,75}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c172459beea6ce775f9a70220175f2df4b1dd0d)
![{\displaystyle \scriptstyle {\sqrt[{3}]{\frac {88,75}{87,75}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f89afe36f298fb687270440da8daa51923aa7d3)










































![{\displaystyle \scriptstyle \left[{\begin{array}{rcl}1054\cdot x&=&\Delta -x\\x&=&101896\ g.\ M.\\x-R&=&5749,2\ g.\ M.\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f15f804bca9c113d95a5d9ef34304618e0589fb)
![{\displaystyle \scriptstyle \left[{\begin{array}{rcl}3500\cdot x^{1}&=&\Delta ^{1}-x^{1};\\x^{1}&=&56285,7\ g.\ M.\\R-x^{1}&=&39861,8\ g.\ M.\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba6af101312c3254d31a3887dee160bf50e91ffd)



















![{\displaystyle \scriptstyle \left[{\frac {2a^{2}}{a^{2}-b^{2}}}-{\frac {a^{2}b}{\left(a^{2}-b^{2}\right)^{\frac {3}{2}}}}\cdot Arc.\sin .{\frac {2b}{a^{2}}}{\sqrt {a^{2}-b^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf213e2ac0efed404481b7b84677ba9668a244e1)




![{\displaystyle \scriptstyle \int \limits _{0}^{2a}\left(1-{\frac {x'}{z'}}dx'\right)=\int \limits _{0}^{2a}\left[1-{\frac {ax'}{\sqrt {2ab^{2}x'+\left(a^{2}-b^{2}\right)x'^{2}}}}\right]dx'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95140e7e096781c0a4fd38e16f69eee0b9a035f9)


![{\displaystyle \scriptstyle \left\{\log \left[{\frac {2ab^{2}+2\left(a^{2}-b^{2}\right)2a}{2{\sqrt {a^{2}-b^{2}}}}}+{\sqrt {2ab^{2}\cdot 2a+\left(a^{2}-b^{2}\right)4a^{2}}}\right]-\log {\frac {2ab^{2}}{2{\sqrt {a^{2}-b^{2}}}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b2fdcc7ab9f78aa40559a2fab15115c48751c30)





































































![{\displaystyle \scriptstyle \left.+{\frac {7}{1024}}\cdot {\frac {x^{12}}{r^{7}}}+{\frac {9}{2048}}\cdot {\frac {x^{14}}{r^{11}}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d829c802659f6dfaff9fd3abae7269d4efb353b)
![{\displaystyle \scriptstyle \times \left[{\frac {1}{\alpha 'r^{2}}}+{\frac {x^{2}}{\alpha '^{2}r^{4}}}+{\frac {x^{4}}{\alpha '^{3}r^{6}}}+{\frac {x^{6}}{\alpha '^{4}r^{8}}}+{\frac {x^{8}}{\alpha '^{5}r^{10}}}+{\frac {x^{10}}{\alpha '^{6}r^{12}}}+{\frac {x^{12}}{\alpha '^{7}r^{14}}}+{\frac {x^{14}}{\alpha '^{8}r^{16}}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e615c0f5bca0037762e64bb22aaebfe9ccf1257)





































![{\displaystyle \scriptstyle \int \limits _{-r}^{+r}y'dx=r^{2}\left\{{\frac {1}{\alpha '}}\left[2-1+{\frac {3}{20}}+{\frac {1}{56}}+{\frac {1}{192}}+{\frac {3}{1408}}+{\frac {7}{6656}}+{\frac {3}{5120}}\right]\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ca4b98f31039239f8d35fa41f2fe2e3358460a)
![{\displaystyle \scriptstyle +{\frac {1}{\alpha '^{2}}}\left[{\frac {2}{3}}-{\frac {3}{5}}+{\frac {3}{28}}+{\frac {1}{72}}+{\frac {3}{704}}\dots \right]+{\frac {1}{\alpha '^{3}}}\left[{\frac {2}{5}}-{\frac {3}{7}}+{\frac {1}{12}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8ef2cdce62fcf89e76b1942201441df39e569b)
![{\displaystyle \scriptstyle \left.+{\frac {1}{\alpha '^{4}}}\left[{\frac {2}{7}}-{\frac {1}{3}}+{\frac {3}{44}}\dots \right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e32b1382e16d39ddd3514d909ac594a1bc243e7)
![{\displaystyle \scriptstyle =r^{2}\left[{\frac {1,17711}{\alpha '}}+{\frac {0,1917}{\alpha '^{2}}}+{\frac {0,054}{\alpha '^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c649f900cbbb947536e314208e6e32eca47160f0)







































![{\displaystyle \scriptstyle S={\frac {1}{2i}}\left\{\left[e^{ix}+e^{2ix}+e^{3ix}+\dots +e^{\nu ix}\right]-\left[e^{-ix}+e^{-2ix}+e^{-3ix}+\dots e^{-\nu ix}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dd9b937782cf6cbd2967c667ea9450bb7ce817e)

![{\displaystyle \scriptstyle ={\frac {1}{2i}}{\frac {e^{(\nu -1)^{ix}}-e^{-(\nu -1)^{ix}}+e^{ix}-e^{-ix}-\left[e^{\nu ^{ix}}-e^{-\nu ^{ix}}\right]}{2-\left[e^{ix}+e^{-ix}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1ba4440e1cb51a7e872e191498fd639db67a8e)































![{\displaystyle \scriptstyle S'={\frac {1}{4}}\left[e^{i2x}+e^{i4x}+\dots +e^{i2nx}\right]+{\frac {1}{4}}\left[e^{-i2x}+e^{-i4x}+\dots +e^{-i2nx}\right]+n\cdot {\frac {2}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42fcc3a517184ab53f6df98e9192a07fd6194cb)
![{\displaystyle \scriptstyle ={\frac {1}{4}}\left[e^{i2x}{\frac {e^{in2x}-1}{e^{i2x}-1}}+e^{-i2x}{\frac {e^{-in2x}-1}{e^{-i2x}-1}}\right]+{\frac {1}{2}}n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08d3867ee92adf2934ce1eca92253971937e2b9)








































![{\displaystyle \scriptstyle {\sqrt[{3}]{\frac {T}{T+L}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e759d3ecddbbdeb83ab89dd841e2a3920387462)
![{\displaystyle \scriptstyle (T+L){\sqrt[{3}]{\frac {T}{T+L}}}={\sqrt[{3}]{T\cdot (T+L)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b980fa5f8e565ba0009415e827213682850d4637)
![{\displaystyle \scriptstyle {\sqrt[{3}]{T\cdot (T+L)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da54fec6f330c4265dcdb64a33a434822fd3e8e3)
![{\displaystyle \scriptstyle {\sqrt[{3}]{\frac {42\cdot 43^{2}}{42^{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b882f03b1c0b597407262dd01d0eaca67619338e)
















































