Auszug aus den Anfangs-Gründen aller Mathematischen Wissenschaften/Die Trigonometrie

1. Die Trigonometrie ist eine Wissenschaft, aus drey gegebenen Theilen eines Triangels, nemlich entweder aus zwey Seiten und einem Winkel, oder aus zweyen Winkeln und einer Seite, oder auch aus allen drey Seiten, die übrigen drey Theile zu finden.[Fig.1]

3. Derowegen stehet der Sinus eines Bogens AD auf dem Radio des Circuls EC perpendicular (§. 95. Geom.); und also sind die Sinus verschiedener Bogen mit einander parallel. (§. 75. Geom.).[Fig.2]
4. Weil der Bogen AE das Maaß des Winkels ACE, und der Bogen AI das Maaß des Winkels ACI ist (§. 16. Geom.); so ist auch AD der Sinus derselben Winkel.[Fig.2]
[176]5. Und also haben zwey Winkel, die neben einander auf einer Linie EI stehen, einerley Sinum.[Fig.2]
6. Die Linie EF, welche auf dem Ende des Radii EC perpendicular ausgerichtet wird, heisset des Bogens AE und folgends des Winkels ECA TANGENS; FC aber desselben Bogens und Winkels SECANS.[Fig.2]
7. Hingegen ED wird sein SINUS VERSUS und AG (= DC) der Sinus des Bogens AH, welcher mit EA 90 Grad machet, der SINUS COMPLEMENTI oder auch COSINUS genennet; der Tangens davon HL TANGENS COMPLEMENTI, oder auch CONTANGENS, ingleichen der Secans CL SECANS COMPLEMENTI oder COSECANS.[Fig.2]
8. Endlich der RADIUS EC heisset der SINUS TOTUS.[Fig.2]
9. Weil der Radius EC der Sinus des Quadranten EH ist; so ist der Sinus totus der Sinus eines rechten Winkels (§. 37. Geom.).[Fig.2]
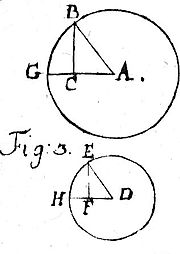
10. Die Sinus ähnlicher Bogen BC und EF haben gegen ihre Radios AB und ED einerley Verhältniß.[Fig.3]
[177]Wenn die Bogen BG und EH einander ähnlich sind; so hat jeder gleich viel Grade, und also sind die Winkel A und D einander gleich (§. 35. Geom.). Nun sind bey C und F rechte Winkel (§. 3.). Derowegen ist, wie der Radius AB zum Sinu BC, so der Radius ED zum Sinu EF (§. 148. Geom.). W. Z. E.
11. Daher hat man dem Sinui toti in einem jeden Circul insgemein 10 000 000 Theile zugeeignet, und durch Hülfe der Geometrie ausgerechnet, wie viel derselben der Sinus und Tangens von jedem Grade, ja einer jeden Minute, durch den ganzen Quadranten bekommet. Und solchergestalt sind die Tabulae Sinuum und Tangentium entstanden, welche man in der Trigonometrie nöthig hat: wie in den Anfangs - Gründen umständlicher gezeiget wird.
12. Weil die Sinus und Tangentes grosse Zahlen sind, welche das Multipliciren und Dividiren in der Trigonometrie sehr beschwerlich machen; so hat Johannes Nepper, ein schottländischer Baron, und nach ihm Heinrich Brigge, ein Engländer, gewisse Zahlen ersonnen, welche man anstatt der ordentlichen Zahlen mit grossem Vortheile in der Rechnung brauchen kan, indem sie das Multipliciren in das Addiren, und das Dividiren in das Subtrahiren verwandeln. Sie werden Logarithmi genennet und sind nicht allein für alle Sinus und Tangentes; sondern auch für die gemeinen Zahlen von 1 bis 10000, zuweilen auch weiter in den gewöhnlichen Tabulis Sinuum und Tangentium zu finden. Von denselben müssen wir noch handeln, ehe wir zu den Aufgaben der Trigonometrie schreiten.
13. Wenn eine Reihe Zahlen in geometrischer Proportion, und eine andere in arithmetischer fortgehen, so heissen die in der letztern die LOGARITHMI der erstern.
[178]14. Es seyn die beide Reihen Zahlen
1. 2. 4. 8. 16. 32. 64. 128. 256. 512. 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.
unter welchen die ersten in einer geometrischen, die andern in einer arithmetischen Proportion fortgehen; so ist 0 der Logarithmus von 1, 1 der Logarithmus von 2, 2 der Logarithmus von 4, 7 der Logarithmus von 128. u. s. w.
15. Wenn der Logarithmus von Eins 0 ist, so ist der Logarithmus des Products gleich der Summe der Logarithmorum der in einander multiplicirten Zahlen. Z. E. 3 die Summe der Logarithmorum 1 und 2 ist der Logarithmus von 8 dem Producte der beiden Zahlen 2 und 4. Wiederum 7 die Summe der Logarithmorum 2 und 5, imgleichen 4 und 3, ist der Logarithmus von 128 dem Producte aus den beiden Zahlen 4 und 32, ingleichen 8 und 16. Daher ist der Logarithmus des Quadrates dem Logarithmo der Wurzel, zweymal genommen, gleich. Z. E. 4 der Logarithmus von der Quadrat-Zahl 16 ist zweymal so groß, wie 2 der Logarithmus von der Wurzel 4; und 6 der Logarithmus von der Quadrat-Zahl 64 ist zweymal so groß, wie 3 der Logarithmus von der Wurzel 8. Hingegen die Hälfte eines Logarithmi ist der Logarithmus der Wurzel aus der ihm zugehörigen Zahl. Also ist die Hälfte des Logarithmi 8 der Logarithmus der Wurzel 16 aus der Quadrat-Zahl 256. Gleichergestalt ist der Logarithmus einer Cubic-Zahl dreymal so groß, wie der Logarithmus der Wurzel. Als 9 der Logarithmus von der Cubic-Zahl 512 ist dreymal so groß, als 3 der Logarithmus von der ihr zugehörigen Wurzel 8. Und daher der Logarithmus der Cubic-Wurzel der dritte Theil des Logarithmi der Cubic-Zahl. Z. E. 2 der Logarithmus von 4 ist der dritte Theil des Logarithmi 6 von der Cubic-Zahl 64.
16. Wenn der Logarithmus von Eins 0 ist; so ist der Logarithmus des Quotienten der Unterscheid zwischen den Logarithmis der beiden Zahlen, die man durch einander dividiret. Und findet man den Logatithmum von einem Bruche, wenn man den Logarithmum des Zehlers von dem Logartithmo des [179] Nenners abziehet, und vor das Ueberbliebene das Zeichen der Subtraction (—) setzet. Also ist 2 der Unterschied zwischen 5 und 7 der Logarithmus des Quotienten 4, welcher heraus kommet, wenn man die dazu gehörigen Zahlen 128 und 32 durch einander dividiret. Ingleichen 5 die Differenz zwischen 3 und 8, ist der Logarithmus von 32 dem Quotienten, der heraus kommet, wenn man 256 durch 8 dividiret. Hingegen — 1, der Unterschied zwischen 0 und 1 ist der Logarithmus von .
17. Hieraus erhellet, wie die Logarithmi das Multipliciren in Addiren, das Dividiren in Subtrahiren, die Ausziehung der Quadrat-Wurzel in Halbiren, und die Ausziehung der Cubic-Wurzel in Dividiren durch 3 verwandeln.
18. Man hat die Logarithmos von 1. 10. 100. 1000. 10000. angenommen 0. 00 000 000, 1. 00 000 000, 2. 00 000 000, 3. 00 000 000, 4. 00 000 000 und auf eine sehr mühsame Art die Logarithmos aller Zahlen von 1 bis 10000, ja nach diesem gar bis 100 000 gefunden, wie in den Anfangs-Gründen gelehret wird. Daraus man ferner die Logarithmos Sinuum und Tangentium gerechnet, wie ebenfalls daselbst zu finden. Wie die Logarithmi gebraucht werden, erhellet aus den folgenden Aufgaben.

19. In einem jeden Triangel ABC verhalten sich die Seiten, wie die Sinus der ihnen entgegen stehenden Winkel.[Fig.4]
Man gedenke sich, es sey der Triangel ABC in einen Circul geschrieben, welches jederzeit geschehen kann (§. 97. Geom.). So ist der halbe Bogen AB das Maaß des Winkels C (§. 84. Geom.), [180] und also ist die halbe Seite AB desselben Sinus (§. 2.). Eben so ist der halbe Bogen AC das Maaß des Winkels B, und daher die halbe Seite AC der Sinus des Winkels B. Derowegen verhält sich, wie die Seite AB zu dem Sinu des ihr entgegen gesetzten Winkels C, also die Seite AC zu dem Sinu des ihr entgegenstehenden Winkels B (§. 59. Arithm.). W. Z. E.
20. Aus der gegebenen Seite AB und zweyen Winkeln A und C die Seite BC zu finden.[Fig.4]
Sprechet (§. 19.):
Wie der Sinus des Winkels C
zu der ihm entgegen gesetzten Seite AB,
So der Sinus des Winkels A
zu der ihm entgegen stehenden Seite BC.
Z. E. Es sey C = 48° 35’, A = 57° 29’ AB = 74’; so verfahret mit den Logarithmis folgendergestalt:
| Log. Sin. C | 9.8750142 |
| Log. AB | 1.8692317 |
| Log. Sin. A | 9.9259487 |
| Summe | 1.1.7918504 |
Log. BC 1.9201662, zu welchem in den Tafeln der Logarithmus von 83’ am nächsten kommet.
[181]
21. Wollet ihr mit 83 Schuhen nicht zufrieden seyn, sondern noch Zolle dazu haben, so suchet diesen Logarithmum unter der Characteristica 2 hinter 830 auf. Alsdenn werdet ihr finden, daß der Logarithmus von 832 ihm am allernächsten kommet, und also über 3 Schuhe noch 2 Zoll sind. Ja wollet ihr gar Linien haben, so suchet euren Logarithmum noch einmal unter Characteristica 3 hinter 8320 auf: so findet ihr, daß der Logarithmus von 8321 ihm am nächsten kommt, und also die Seite BC 8° 3’ 2’’ 1’’’ sey. Und solchergestalt müsset ihr allezeit verfahren, wenn der Logarithmus einer Seite unter seiner Characteristica nicht vollkommen zu finden.
22. Weil die Auflösung der Aufgabe durch die Regel Detri geschiehet (§. 85. Arithm.), und daher der Sinus A mit der Seite AB multipliciret, das Product aber durch den Sinum des Winkels C dividiret werden solte; so ist klar, daß man den Logarithmum von AB zu dem Logarithmo des Sinus A addiren, und von der Summe den Logarithmum des Sinus C abziehen muß (§. 15. 16.).
23. Aus zwey gegebenen Seiten AB und BC, und einem Winkel C, der einer von ihnen entgegen stehet, die übrigen Winkel zu finden.
Sprechet (§. 19.):[Fig.4]
Wie die Seite AB
zu dem Sinu des entgegen stehenden Winkels C;
So die Seite BC
zu dem Sinu des entgegen stehenden Winkels A.
[182] Z. E. Es sey AB = 82’, BC = 75’, C = 64° 33’.
Verfahret also:
| Log. AB | 1.9138138 |
| Log. Sin. C | 9.9556688 |
| Log. BC | 1.8750613 |
| Summe | 1.1.8307301 |
Log. Sin. A 99169163, zu welchem in den Tafeln der Logarithmus von 55° 40’ am nächsten kommet.
24. Seyd ihr mit 55° 40’ nicht zufrieden; so könnet ihr noch Secunden dazu suchen. Ziehet nemlich von eurem
| Logarithmo | 9.9169163 | |
| den nächst-kleineren | 9.9168593 | ab und |
| merket die erste Differenz | 570 |
Imgleichen
| von dem nächst-grösseren | 99169455 | |
| den nächst-kleineren | 99168593 | und |
| merket die andere Differenz | 862. |
| Sprechet: 862 geben 60’’ wie viel geben | 570 |
| 60 | |
| 34200 |
- 3.4.2.00(39’’
- 862)25 86
- 8.3.4.0
- 7 7 5 8
- 5 8 2
So bekommet ihr noch 39’’; und also ist der Winkel A 55° 40’ 39’’.
[183]25. Wenn ihr zwey Winkel A und C habet, könnet ihr den dritten durch die Geometrie finden (§. 77. Geom.); wie aus beygefügtem Exempel zu ersehen.
| C | 64° | 33’ | 0’’ |
| A | 55 | 40 | 39 |
| A+C | 120 | 13 | 39 |
| A+C+B | 179 | 59 | 60 |
| B | 59 | 46 | 21. |

26. Aus zweyen Seiten AB und BC, die in einem rechtwinkelichten Triangel den rechten Winkel B einschliessen, die Winkel zu finden.[Fig.5]
Nehmet BC für den Sinum totum an; so ist AB der Tangens des Winkels C (§. 6.). Sprechet demnach:
Wie die Seite BC
zu der Seite AB;
So verhält sich der Sinus totus
zu dem Tangente des Winkels C.
Z. E. Es sey BC 79’; AB 54’; so geschiehet die Rechnung also:
| Log. BC | 1.8976271 |
| Log. AB | 1.7323938 |
| Log. Sin. tot. | 1.00000000 |
Log. Tang. C. 9.8347667, welchem in den Tafeln am nächsten kommet der Logarithmus Tangentis von 34° 21’. Demnach ist der [184] Winkel C 34° 21’; der Winkel A aber 55° 39’ (§. 75. Geom.).
27. Wenn man zu der halben Summe zweyer Zahlen oder Grössen die halbe Differenz addiret, so kommet die grössere von ihnen heraus: subtrahiret man aber dieselbe von ihr, so bleibet die kleinere übrig.
Die grössere Zahl bestehet aus der kleinern und ihrer Differenz von der grössern; und also die Summe beider aus der Differenz und der kleinern zweymal genommen. Da nun die halbe Summe aus der kleinern und der halben Differenz bestehet, so kommet die grössere heraus, wenn man die halbe Differenz dazu addiret: hingegen bleibet die kleinere übrig, wenn man sie subtrahiret. W. Z. E.

28. Aus zwey gegebenen Seiten eines Triangels AC und CB nebst dem Winkel C, den sie einschliessen, die übrigen Winkel zu finden.[Fig.6]
1. Sprechet:
Wie die Summe der beiden Zahlen AC und CB
zu ihrer Differenz:
So der Tangens der halben Summe der beiden
gesuchten Winkel A und B
zu dem Tangente der halben Differenz derselben.
[185] 2. Addiret diese halbe Differenz zu der halben Summe; so habet ihr den Winkel B, welcher der grösten von den gegebenen Seiten entgegen gesetzet ist. Subtrahiret sie von derselben; so bleibet der Winkel A übrig (§. 27.).
Z. E. Es sey AC 75’, BC 58’, C 108° 24’; so geschiehet die Rechnung folgender massen:
| AC | = | 75’ | AC | = | 75’ | A+B+C | = | 179° 60’ |
| BC | = | 58 | BC | = | 58 | C | = | 108° 24’ |
| ___________ | _____________ | ________________ | ||||||
| AC+BC | 133’ | AC-BC | 17’ | A+B | 71° 36’ | |||
| (A+B) | 35° 48’ | |||||||
| Log. AC+BC | 2.1238516 |
| Log. AC-BC | 1.2304489 |
| Log. Tang. (A+B) | 9.8580694 |
| Summe | 1.1.0885183 |
| Log. Tang. (A-B) | 8.9646667’ |
dem in den Tafeln der Logarithmus Tangentis von 5° 17’ am nächsten kommet.
| (A+B) | 35° 48’ | (A+B) | 35° 48’ | ||
| (A-B) | 5 17 | (A-B) | 5 17 | ||
| _______________ | _______________ | ||||
| B | 41° 5’ | A | 30° 31’ | ||
Verlängert die Seite AC in D bis CD = BC, und machet CE = CB; so ist DA die Summe, EA die Differenz der beiden Seiten CB und CA, und DBE ein rechter Winkel (§. 86. Geom.). Man ziehe AG mit EB parallel; so ist bey G auch [186] ein rechter Winkel und GAD = BED (§. 37. 72. Geom.), imgleichen GB der Tangens des Winkels GAB und GD der Tangens des Winkels GAD (§. 6.). Nun ist DCB = CBA + CAB = CBE + CEB = 2 CEB (§. 74. 79. Geom.), und also CEB, imgleichen CAG die halbe Summe der gesuchten Winkel CBA und CAB, folgends BAG die halbe Differenz (§. 27.). Derowegen verhält sich wie DA die Summe der beiden Seiten zu EA ihrer Differenz, also DG der Tangens der halben Summe der gesuchten Winkel zu BG dem Tangente der halben Differenz (§. 149. Geom.). W. Z. E.

29. Aus drey gegebenen Seiten eines Triangels die Winkel zu finden.[Fig.7]
1. Beschreibet aus der Spitze des Triangels A mit der kleinen Seite AB einen Circul; so ist CD [weil AB = AD (§. 27. Geom.)] die Summe zweyer Seiten, FC ihre Differenz.
2. Sprechet: wie die Grundlinie des Triangels BC zu der Summe der beiden Seiten AB + AC;
So ihre Differenz FC
zu dem Stücke der Grundlinie GC.
3. Ziehet GC von der Grundlinie BC ab; so bleibet BG übrig.
4. Lasset aus A ein Perpendicul AE auf BG fallen; so ist BE = EG = BG (§. 95. Geom.), und ihr könnet aus den beiden Seiten AB und BE in dem rechtwinkelichten Triangel ABE die Winkel [187] B und A; und in dem andern AEC aus den beiden Seiten AC und EC die Winkel C und A (§. 23.) finden.
Z. E. Es sey AB = 36’, AC = 45’, BC = 40’.
Die Rechnung geschiehet folgendermassen:
AB 36’ AC 45’ AC 45 AB 36 _________ ______ AB+AC 81 FC =9
Log. BC 1.6020600 Log. AB+AC 1.9084850 Log. FC 0.9542425 Summe 2.8627275
Log. CG 1.2606675, welchem in den Tafeln der Logarithmus von 18 am nächsten kommet. Wenn man aber weiter nachsuchet (§. 21.); findet man endlich GC 1822’’’
BC 4000’’’ EG 1089’’’ GC 1822 GC 1822 _________ _________ BG 2178’’’ EC 2911’’’ _________ BE 1089’’’
Log. AB 3.5563025 Log. Sin. tot. 10.0000000 Log. EB 3.0370279
Log. Sin. A. 9.4807254, welchem in den Tafeln der Logarithmus von 27° 36’ am nächsten kommet. Und also ist B 72° 24’. [188]
Log. AC 3.6532125 Log. Sin. tot. 10.0000000 Log. Sin. EC 3.4640422
- Log. Sin. A 9.8108297, welchem in den Tafeln der Logarithmus von 40° 19’ am nächsten kommet. Und also ist der Winkel C 49° 41’.
Solchergestalt sind in dem Triangel ABC der Winkel A 57° 55’, B 72° 24’ und C 49° 41’.
Es ist weiter nichts zu erweisen, als daß sich CB zu CD wie CF zu CG verhält, welches auf folgende Weise geschiehet.[Fig.7]
Da y oder CBD zu seinem Maasse den halben Bogen GFD, und x zu seinem den halben Bogen GBD hat (§. 84. Geom.); so ist x + y = 180°. Nun ist auch x + o = 180° (§. 38. Geom.). Derowegen ist o = y (§. 25. Arithm.). Da ferner der Winkel C den beiden Triangeln CGF und CBD gemein ist; so ist CE : CD = CF : CG (§. 148. Geom.). W. Z. E.
30. Weil BE und EC in Linien gegeben sind; so muß man auch in der Rechnung anstatt 36’ für AB 3600’’’ und anstatt 45’ für AC 4500’’’ annehmen.
31. Wir wollen noch mit wenigem den Nutzen der Trigonometrie in Auflösung einiger geometrischen Aufgaben zeigen.

32. Eine Höhe AB (z. E. eines Thurms) [189] zu messen, zu der man aus einem angenommenen Stande E kommen kan.[Fig.8]
1. Messet den Winkel ADC (§. 43. Geom.) und die Linie BE oder DC (§. 44. Geom.).
2. So wisset ihr auch den Winkel A, weil bey C ein rechter Winkel ist (§. 75. Geom.).
3. Suchet alsdenn die Linie AC (§. 20.), und
4. addiret dazu die Höhe des Instruments DE (= BC, weil die Linien CD und BE parallel, und CB und ED auf BE perpendicular sind); so kommet die Höhe AB heraus. Wäre aber BE nicht horizontal; so müste man das Stücke BC besonders messen. (§. 171. Geom.).

33. Eine Höhe AB zu messen, zu der man nicht kommen kan.[Fig.9]
1. Erwählet euch zwey Stände in E und G, um so viel weiter von einander, je höher der Berg oder der Thurm ist, den ihr messen wollet, und messet aus denselben die Winkel ADC und AFC (§. 43. Geom.), über dieses die Standlinie GE oder DF (§. 44. Geom.).
2. Ziehet von dem Winkel ADC den Winkel AFC ab; so bleibet der Winkel FAD übrig (§. 74. Geom.).
3. Suchet aus den nunmehro bekannten Winkeln und der Seite FD in dem Triangel AFD die Seite AF, und
4. aus dem Winkel F und der Seite AF in [190] dem rechtwinkelichten Triangel die Seite AC (§. 20.).
5. Endlich addiret zu der Höhe AC die Höhe des Instruments DE, oder, wenn BC der Höhe des Instruments nicht gleich ist, so suchet ferner FC und endlich BC im Triangel FBC (§. 20.); so habet ihr die verlangte Höhe AB.

34. Aus zwey Fenstern E und F in verschiedenen Stockwerken eines Gebäudes eine Höhe zu messen, deren Spitze A man aus beiden Fenstern sehen kan.[Fig.10]
1. Messet durch einen Bleywurf die Höhe des andern Fensters über dem ersten EF, und des ersten über der Erde FG, und aus den Fenstern die Winkel AEC und AFD (§. 43. Geom.).
2. Addiret den Winkel AEC zu 90°, so habet ihr den Winkel AEF; subtrahiret von 90° den Winkel AFD, so bleibet der Winkel AFE übrig.
3. Addiret die beiden Winkel AEF und AFE, und ziehet die Summe von 180° ab; so bleibet der Winkel EAF übrig (§. 77. Geom.).
4. Suchet in dem Triangel AEF die Seite AF, und ferner
5. in dem Triangel AFD die Seite AD (§. 20.).
6. Endlich addiret dazu die Höhe des Fensters FG von der Erde; oder, wenn GB nicht horizontal ist, suchet ferner DF, und hernach vermittelst des Winkels DEB, den ihr gemessen (§. 43. [191] Geom.), DB besonders (§. 20.); so kommet die Höhe AB heraus.

35. Die Weite zweyer Oerter, zu deren beiden man aus einem angenommenen Stande kommen kan, zu messen.[Fig.11]
1. Messet den Winkel C (§. 43. Geom.) und die Linie AC und CB (§. 44. Geom.): so könnet ihr
2. den Winkel A (§. 28.) und endlich die verlangte Weite AB (§. 20.) finden.
36. Die Weite zweyer Oerter AB, zu deren einem B man aus einem angenommenen Stande C nur kommen kan (z. E. die Breite eines Flusses) zu messen.[Fig.12]
1. Messet die beiden Winkel B und C (§. 43. Geom.) und die Standlinie BC (§. 44. Geom.); so könnet ihr
2. die verlangte Weite AB (§. 20.) finden.
37. Die Weite zweyer Oerter AB, zu deren keinem man kommen kan, zu finden.[Fig.13]
1. Erwählet drey Stände, D, C und E in einer Linie, und messet die Winkel ADC, ACD, BCE und BEC (§. 43. Geom.), nebst den beiden Standlinien DC und CE (§. 44. Geom.).
2. Subtrahiret die beiden Winkel ADC und [192] ACD, wiederum ACD und BCE, und abermal BCE und BEC von 180°; so bleibet im ersten Falle der Winkel DAC, im andern der Winkel ACB, und im dritten der Winkel CBE übrig (§. 77. 38. Geom.). Alsdenn könnet ihr
3. die Seiten AC und BC (§. 20.), und so ferner
4. den Winkel CAB (§. 28.) und endlich die Seite AB (§. 20.) finden.

38. Die Verhältniß des Diametri eines Circuls zu seiner Peripherie zu finden.[Fig.14]
Wenn der Radius des Circuls CD 10000000 ist; so ist sowohl der Sinus AG, als Tangens ED des Bogens von einer Minute DA beynahe 2909; und also muß der Bogen AD, welcher sonst etwas grösser ist als AG, und kleiner als ED, gleichfalls beynahe 2909 seyn. Multipliciret 2909 durch 21600, das ist die Zahl der Minuten in der ganzen Peripherie: so ist das Product 62834400. Derowegen verhält sich der Diameter zu der Peripherie beynahe wie 20000000 zu 62834400, das ist, (wenn man beiderseits mit 200000 dividiret,) wie 100 zu 314 (§. 59. Arithm.).
