Über die Streuung von Licht an Licht nach der Diracschen Theorie

Über die Streuung von Licht an Licht nach der Diracschen Theorie^[1]

Von Hans Euler

(Mit 3 Figuren)

Inhalt: Einleitung. — I. Teil: §1. Vorläufige Angabe eines anschaulichen Ausdrucks für die Wechselwirkung ${\bar {U}}_{1}$ von Licht mit Licht, welche zum Übergang zweier Lichtquanten $g_{1}$, $g_{2}$ in zwei andere $-g_{3}$, $-g_{4}$ führt:

$\left((g_{1}g_{2}|{\bar {U}}_{1}|-g_{3}-g_{4})=H_{in}^{4}\right)$;

§2. Nähere Bestimmung der Wechselwirkung ${\bar {U}}_{1}$ von Licht mit Licht aus der Invarianz der dazugehörigen korrigierten Maxwellschen Gleichungen:

$\left({\bar {U}}_{1}={\frac {\hbar c}{c^{2}}}{\frac {1}{{E_{0}}^{2}}}\int [\alpha ({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2})^{2}+\beta ({\mathfrak {B}}{\mathfrak {D}})^{2}]dV\right)$;

§3. Diskussion der Vertauschungsrelationen für die Feldstärken im System der korrigierten Maxwellgleichungen. — II. Teil: §4. Allgemeines Störungsschema, das zur Berechnung der Streuung von Licht an Licht verwandt wird; §5. Aufstellung der Matrix $H_{in}^{4}$ der Diracschen Theorie für Streuung von Licht an Licht; §6. Entwicklung nullter Ordnung dieser Matrix $H_{in}^{4}$ nach Lichtfrequenzen und Vergleich mit dem Heisenbergschen Subtraktionsglied; §7. Nachweis der Identität der aus der Diracschen Theorie folgenden Matrix $H_{in}^{4}$ mit der oben aufgestellten Wechselwirkungsenergie ${\bar {U}}_{1}$ der Lichtquanten. — III. Teil: §8. Ausrechnung des Matrixelements für Streuung von Licht an Licht (im Glied 4. Ordnung der Entwicklung nach Lichtfrequenzen) für zwei Spezialfälle zur Bestimmung der Zahlenkoeffizienten $\alpha$, $\beta$ in der Wechselwirkung von Licht mit Licht. $\left(\alpha =-{\tfrac {1}{360\pi ^{2}}},\beta =-{\tfrac {7}{360\pi ^{2}}}\right)$; §9. Bestätigung des Verfahrens; §10. Diskussion des Resultats.

---

Einleitung

Halpern^[2] und Debye^[3] haben bemerkt, daß man nach der Diracschen Theorie eine Streuung von Licht an Licht erwarten muß. Denn zwei Lichtquanten können ein Paar, ein Positron und ein Elektron, erzeugen und dieses Paar kann sofort wieder zerstrahlen; zwei Lichtquanten können sich also spontan in zwei andere Lichtquanten verwandeln (unter Erhaltung von Energie- und Impulssumme).

Bei diesem Prozeß muß man zwei Fälle unterscheiden:

Entweder die Energien $c\,g^{1}$ und $c\,g^{2}$ der beiden Lichtquanten und der Winkel zwischen ihren Impulsen ${\mathfrak {g}}^{1}$, ${\mathfrak {g}}^{2}$ sind so groß, daß Energie und Impulssatz die Erzeugung eines wirklichen Paars erlauben $\left(g^{1}g^{2}-({\mathfrak {g}}^{1}{\mathfrak {g}}^{2})>2(mc)^{2}\right)$. Dann erhält man die Wahrscheinlichkeit der Streuung der Lichtquanten aneinander, indem man die Wahrscheinlichkeiten der Paarerzeugung und der Wiederzerstrahlung multipliziert und über alle Möglichekeiten summiert. Dies ist von Breit und Wheeler^[4] durchgeführt worden.

Oder aber Energie und Impuls zweier Lichtquanten reichen nicht zur Erzeugung eines wirklichen Paars aus

(0,1)

${\begin{pmatrix}g^{1}g^{2}-({\mathfrak {g}}^{1}{\mathfrak {g}}^{2})<2(m\,c)^{2},\\{\text{d.h. in geeignetem Bezugssystem: }}g^{1}<m\,c,g^{2}<m\,c\end{pmatrix}}.$

Dann können die Lichtquanten $g^{1}$, $g^{2}$ doch durch die virtuelle Möglichkeit der Paarerzeugung in zwei andere Lichtquanten übergehen und auch in diesem Fall (etwa des sichtbaren Lichts) muß es eine Streuung von Licht an Licht geben. Ihr Wirkungsquerschnitt soll hier berechnet werden. (§ 10, Formel 9 und 10).

I. Teil

Die Wahrscheinlichkeit des Übergangs zweier Lichtquanten ${\mathfrak {g}}^{1}$, ${\mathfrak {g}}^{2}$ in zwei andere $-{\mathfrak {g}}_{3}$, $-{\mathfrak {g}}_{4}$ wird gegeben durch das Quadrat eines Matrixelements $H_{in}^{4}$ der Diracschen Theorie (welches, wie sich später zeigen wird, von 4. Ordnung in der Elektronenladung ist).

Die direkte Ausrechnung dieser Matrix $H_{in}^{4}$ der Diracschen Theorie (Teil II, III), [d.h. der Matrixelemente, für den allgemeinen Fall beliebiger Streu- und Polarisationsrichtungen] würde sehr mühsam sein. Sie kann jedoch auf das einfachere Problem der Berechnung zweier Matrixelemente [d.h. der Berechnung von $H_{in}^{4}$ für zwei spezielle Streu- und Polarisationsrichtungen] zurückgeführt werden durch die folgenden allgemeinen Betrachtungen (Teil I).

§1. Vorläufige Angabe eines anschaulichen Ausdrucks für die Wechselwirkung ${\bar {U}}_{1}$ von Licht mit Licht, welche zum Übergang zweier Lichtquanten $g_{1},g_{2}$ in zwei andere $-g_{3},-g_{4}$ führt.

$\left((g_{1}g_{2}|U_{1}|-g_{3}-g_{4})=H_{in}^{4}\right).$

Wenn zwei Lichtwellen sich aneinander streuen, statt sich ungestört zu überlagern, so bedeutet das eine Abweichung vom Superpositionsprinzip. Das optische Superpositionsprinzip wird durch die Linearität der Maxwellschen Gleichungen des Vakuums zum Ausdruck gebracht. Die Streuung von Licht an Licht wird also durch einen nichtlinearen Zusatz zu den Maxwellschen Vakuumsgleichungen beschrieben werden können, falls eine anschauliche Beschreibung möglich ist. Diese anschauliche Beschreibung, deren Möglichkeit wir später (§7) nachweisen, wird durch die folgende Analogie nahegelegt, welche in der Diracschen Theorie zwischen Lichtquanten und Elektronen besteht:

Zwei Elektronen können Lichtquanten erzeugen und dadurch in gegenseitige Wechselwirkung treten, die sich etwa in der Streuung der Elektronen aneinander äußert und für die es in gewisser Näherung einen anschaulichen Ausdruck, das Coulombsche Gesetz gibt.

Ebenso erzeugen zwei Lichtquanten virtuell eine Menge von Paaren und dadurch entsteht zwischen ihnen eine Wechselwirkung, die zur Streuung von Licht an Licht führt. Auch für diese Wechselwirkung der Lichtquanten miteinander sollte man einen dem Coulombschen Gesetz analogen, einfachen, anschaulichen Ausdruck erwarten.

Die Coulombsche Wechselwirkung in einem Materiefeld, das durch einen Dichteoperator $\psi ^{\ast }\psi$ beschrieben wird, ist

(1,1)

${\bar {U}}'={\frac {e^{2}}{2}}\iint {\frac {\psi ^{\ast }(\xi )\psi (\xi )\psi ^{\ast }(\xi ')\psi (\xi ')}{(\xi -\xi ')}}dV\,dV'$

Den Wirkungsquerschnitt für die Streuung eines Elektrons an einem Elektron erhält man aus dem Quadrat des Matrixelements von (1,1) für einen Übergang im Materiefeld, der die Streuung zweier Elektronen aneinander bedeutet.

Um eine zu (1,1) analoge Wechselwirkung der Lichtquanten zu finden, muß man eine Funktion ${\bar {U}}_{1}$ der Freiheitsgrade des Strahlungsfeldes, also der Feldstärken $F_{ik}$ suchen, deren Matrixelement für einen Übergang im Strahlungsfeld, welcher die Streuung zweier Lichtquanten aneinander bedeutet, gleich dem oben besprochenen und später zu berechnenden Matrixelement $H_{in}^{4}$ der Diracschen Theorie für diesen Prozeß ist. Über diese Wechselwirkung ${\bar {U}}_{1}$ der Lichtquanten als Funktion der Feldstärken läßt sich folgendes aussagen:

Da sie zu Prozessen führen soll, in denen zwei Lichtquanten vergehen und zwei entstehen, muß sie die Feldstärken oder ihre Ableitungen in der 4. Potenz enthalten:

${\bar {U}}_{1}={\text{const}}\int \left[FFFF+{\text{const'}}{\frac {\partial F}{\partial x}}{\frac {\partial F}{\partial x}}FF+\cdots \right]dV$

(Indices von Tensoren und Vektoren sind hier und im folgenden weggelassen oder durch spezielle Indices repräsentiert, um ihre Verknüpfung zu einem Skalar noch offen zu halten).

Da die Wechselwirkung ${\bar {U}}_{1}$ die Dimension einer Energie haben, aber (als Glied 4. Ordnung der Diracschen Theorie) die Elektronenladung in der 4. Potenz enthalten soll (und da aus den 4 universellen Einheiten $e$, $m$, $c$, $h$ nur eine dimensionslose Zahl, die Sommerfeldsche Feinstrukturkonstante ${\tfrac {e^{2}}{\hbar c}}\sim {\tfrac {1}{137}}$ gebildet werden kann), ist die Konstante bis auf einen numerischen Faktor bestimmt zu:

(1,2)

$\left\{{\begin{array}{c}{\text{const}}={\dfrac {\hbar c}{e^{2}}}{\dfrac {1}{{E_{0}}^{2}}}\\{\text{mit }}E_{0}={\dfrac {e}{\left({\dfrac {e^{2}}{mc^{2}}}\right)^{2}}}={\text{,,Feldstärke am Rande des Elektrons''}}.\end{array}}\right.$

Aus demselben Grunde müssen die Glieder mit den Ableitungen der Feldstärken noch eine von der Elektronenladung unabhängige Länge, also die Comptonwellenlänge ${\tfrac {h}{m\,c}}$ als zusätzlichen Faktor enthalten.

Zunächst wundert man sich darüber, daß in der Vakuumelektrodynamik die Elektronenmasse vorkommen soll, während doch vorausgesetzt ist, daß nur Lichtquanten und gar keine Elektronen vorhanden sind. Obwohl aber die hier betrachten Glieder nur Gültigkeit haben, solange keine wirklichen Paare erzeugt werden, kommen sie doch nur durch die virtuelle Möglichkeit der Paarerzeugung zustande und das äußert sich im Auftreten der Elektronenmasse.

Man erwartet also neben der Maxwellschen Energie der einzelnen Lichtquanten eine gegenseitige Wechselwirkung der Lichtquanten von der Form:

(1,3)

${\bar {U}}_{1}={\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\int \left[FFFF+\left({\frac {\hbar }{mc}}{\frac {\partial }{\partial x}}F\right)\left({\frac {\hbar }{mc}}{\frac {\partial }{\partial x}}F\right)FF+\cdots \right]dV.$

Es wird später gezeigt werden, daß das oben besprochene Matrixelement $H_{in}^{4}$, das aus der Diracschen Theorie folgt, auch wirklich in das Matrixelement eines solchen Ausdrucks (1,3) umgeformt werden kann.

Da wir uns auf weiches Licht $(|g|<mc)$ also auf langsam veränderliche Felder $\left(\left|{\frac {\hbar }{mc}}{\frac {\partial F}{\partial x}}\right|<|F|\right)$ beschränken wollen (0,1), können wir in (1,3) die Glieder mit den Ableitungen der Feldstärken fortlassen.

Wir nehmen also jetzt, vorbehaltlich des späteren Beweises (§7) an, daß die Streuung von weichem Licht an Licht durch eine (zur Maxwellschen zusätzliche Energiedichte im Strahlungsfeld von der Form

(1,4)

$U_{1}={\frac {\hbar c}{e^{2}}}{\frac {1}{E_{0}^{2}}}FFFF$

beschrieben werden kann:

(1,5)

$H_{in}^{4}=\left(g_{1}g_{2}\left|\int U_{1}dV\right|-g_{3}-g_{4}\right).$

($F_{ik}$ Feldstärken, $V$ Volumen des Strahlungsraums, $E_{0}={\frac {e}{\left({\frac {e^{2}}{mc^{2}}}\right)^{2}}},$

$g_{1}g_{2}$	Lichtquanten vor dem Stoß
$-g_{3}-g_{4}$	Lichtquanten nach dem Stoß
$(g_{1}g_{2}|0|-g_{3}-g_{4}$	Matrixelement des Operators 0 für diesen Übergang
$H_{in}^{4}$	Matrixelement der Diracschen Theorie für diesen Übergang.

§2. Nähere Bestimmung der Wechselwirkung ${\bar {U}}_{1}$ von Licht mit Licht aus der Invarianz der dazugehörigen korrigierten Maxwellschen Gleichungen

$\left({\bar {U}}_{1}={\frac {\hbar c}{e^{2}}}{\frac {1}{E_{0}^{2}}}\int \left[\alpha ({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2})^{2}+\beta ({\mathfrak {BD}})^{2}\right]dV\right)$^[5].

Die Gestalt dieser Wechselwirkung $U_{1}$ (1,4) von Licht mit Licht soll nun durch die Forderung der relativistischen Invarianz näher bestimmt werden.

In der allgemeinen Quantentheorie von Licht mit Materie^[6] genügt der Tensor der elektrischen Feldstärke und magnetischen Induktion, die hier mit ${\mathfrak {E}}$, ${\mathfrak {B}}$ bezeichnet werden sollen, den Gleichungen:

(2,1)

${\begin{array}{|c|}\hline \\{\frac {1}{e}}{\dot {\mathfrak {B}}}+{\textrm {rot}}{\mathfrak {E}}=0,\qquad {\textrm {div\,}}{\mathfrak {B}}=0\\\\\hline \end{array}}$,

welche mit der Existenz von Potentialen ${\mathfrak {A}}$ gleich bedeutend sind:

(2,2)

${\begin{array}{|c|}\hline \\{\mathfrak {E}}=-{\frac {1}{c}}{\dot {\mathfrak {A}}},\qquad {\mathfrak {B}}={\textrm {rot}}\,{\mathfrak {A}}\\\\\hline \end{array}},$

und den Gleichungen

(2,3)

${\begin{array}{|c|}\hline \\-{\frac {1}{c}}{\dot {\mathfrak {E}}}+{\textrm {rot}}\,{\mathfrak {B}}={\frac {4\pi i}{c}},\qquad {\textrm {div}}\,{\mathfrak {E}}=4\pi \varrho \\\\\hline \end{array}}$

welche das Feld ${\mathfrak {E}},{\mathfrak {B}}$ mit der Materie der Dichte $\varrho$ und der Strömung $i$ verknüpfen. Die Materie $\varrho ,i$ ist ihrerseits wieder durch die Diracgleichung in ihrem Ablauf und ihrer Rückwirkung auf das Feld bestimmt.

Diese allgemeinen Zusammenhänge (2,1; 2,2; 2,3) bestehen vor wie nach der Löchertheorie.

Etwas neues entsteht durch die Löchertheorie aber beim Versuch der folgenden Spezialisierung.

Wenn keine Elektronen vorhanden sind, konnte man vor der Löchertheorie $\varrho$ und $i$ streichen und erhielt die Maxwellschen Gleichungen des Vakuums: (2,1) oder (2,2) und

(2,4)

$-{\frac {1}{c}}{\dot {\mathfrak {E}}}+{\textrm {rot}}\,{\mathfrak {B}}=0,\qquad {\textrm {div}}\,{\mathfrak {E}}=0.$

(2,5)

In der Löchertheorie aber kommt, auch wenn keine Elektronen vorhanden sind und auch wenn die Energie des Strahlungsfeldes nicht ausreicht, um Elektronen und Positronen zu erzeugen,

doch, wie wir sahen, die virtuelle Möglichkeit zur Erzeugung von Materie im Verhalten des Feldes zum Ausdruck.

Die Gleichung für diesen Spezialfall (2,5) müssen einerseits mit den allgemeinen Gleichungen (2,1; 2,2; 2,3) im Einklang sein, andererseits die Feldstärken allein enthalten; sie können also nur dadurch aus (2,1; 2,2; 2,3) hervorgehen, daß die Ströme $\varrho ,i$ durch gewisse Funktionen der Feldstärken ${\mathfrak {E}},{\mathfrak {B}}$ ersetzt werden, die man als „die vom Feld ${\mathfrak {E}},{\mathfrak {B}}$ virtuell erzeugte Materie“ bezeichnen kann.

D. h.: Für unseren Spezialfall (2,5) bleiben die Gleichungen (2,1; 2,2) bestehen, aber die Maxwellschen Vakuumgleichung (2,4) sind durch gewisse Zusätze zu korrigieren, welche nur bei (gegen $E_{0}$) kleinen Feldern vernachlässigt werden dürfen.

Wir nehmen an, daß die abgeänderten Feldgleichungen durch eine Hamiltonfunktion ${\bar {U}}$ und ihre kanonischen Gleichungen beschrieben werden können. Als Koordinaten des Systems können wir (nach 2,2) das (negative) Vektorpotential $-{\mathfrak {A}}$ wählen. Die zu $-{\mathfrak {A}}$ kanonisch konjugierten Impulse sollen ${\mathfrak {D}}/4\pi c$ heißen, also durch

(2,6)

${\mathfrak {D}}_{i}(\xi ){\mathfrak {A}}_{k}(\xi ')-{\mathfrak {A}}_{k}(\xi '){\mathfrak {D}}_{i}(\xi )=2hci\delta (\xi -\xi ')\delta _{ik}$

oder

(2,7)

${\begin{array}{|c|}\hline \\{\mathfrak {D}}_{i}(\xi ){\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi '){\mathfrak {D}}_{i}(\xi )=2hci{\frac {\partial }{\partial \xi _{i}'}}\delta (\xi -\xi ')\\\\\hline \end{array}}$

(mit zyklischen $ikl$) definiert sein.

Die Energie ${\bar {U}}$ ist dann eine Funktion aller Koordinaten und Impulse,

(2,8)

${\begin{array}{|c|}\hline \\{\bar {U}}=\int UdV\\\\\hline \end{array}}$

die allerdings nur die Feldstärken, nicht aber ihre Ableitungen enthalten soll:

(2,9)

$U=U({\mathfrak {B,D}}).$.

Die kanonischen Gleichungen zur Hamiltonfunktion ${\bar {U}}$ werden nun:

${\begin{aligned}{\dot {\mathfrak {B}}}_{k}(\xi ')&={\frac {i}{\hbar }}\int \left[U{\big (}{\mathfrak {B}}(\xi ),{\mathfrak {D}}(\xi ){\big )}{\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi ')U{\big (}{\mathfrak {B}}(\xi ),{\mathfrak {D}}(\xi ){\big )}\right]d\xi \\&=-4\pi c\,{\textrm {rot}}_{k}{\frac {\partial U}{\partial {\mathfrak {D}}}}\end{aligned}}$

oder mit (2,1):

(2,10)

${\begin{array}{|c|}\hline \\{\frac {\partial U}{\partial {\mathfrak {D}}}}={\frac {\mathfrak {E}}{4\pi }}\\\\\hline \end{array}}$

und:

${\begin{aligned}{\dot {\mathfrak {D}}}_{k}(\xi ')&={\frac {i}{\hbar }}\int \left[U{\big (}{\mathfrak {B}}(\xi ),{\mathfrak {D}}(\xi ){\big )}D_{k}(\xi ')-{\mathfrak {D}}_{k}(\xi ')U{\big (}{\mathfrak {B}}(\xi ){\mathfrak {D}}(\xi ){\big )}\right]d\xi \\&=4\pi c\,{\textrm {rot}}_{k}{\frac {\partial U}{\partial {\mathfrak {B}}}}\end{aligned}}$

oder mit der Definition

(2,11)

${\begin{array}{|c|}\hline \\{\frac {\partial U}{\partial {\mathfrak {B}}}}={\frac {\mathfrak {H}}{4\pi }}\\\\\hline \end{array}}$

(2,12)

${\begin{array}{|c|}\hline \\-{\frac {1}{c}}{\dot {\mathfrak {D}}}+{\textrm {rot}}\,{\mathfrak {H}}=0\\\\\hline \end{array}}$

was weiter

${\begin{array}{|c|}\hline \\{\textrm {div}}\,{\mathfrak {D}}=0\\\\\hline \end{array}}$

erlaubt. Damit sind zu jeder Energie $U$ die Feldgleichungen festgelegt: (2,1) und (2,12) gibt den zeitlichen Ablauf des Feldes, (2,10) und (2,11) verknüpft die Feldstärke ${\mathfrak {E,B}}$ mit den Feldfunktionen ${\mathfrak {D,H}}$. Wie die Gl. (2,12) und (2,1) zeigen, bedeutet ${\mathfrak {D}}$ die elektrische Verschiebung ${\mathfrak {B}}$ die magnetische Induktion und als solche die Kraft auf den wahren Strom^[7].

Das allgemeine Schema (2,1; 2,2; 2,12; 2,10; 2,11), das nur auf dem Induktionsgesetz (2,1) und der Abhängigkeit der Energie von den Feldstärken allein beruht, bekommt seinen Inhalt erst durch die Angabe einer bestimmten Hamiltonfunktion $U$.

Ist $U={\frac {{\mathfrak {B}}^{2}+{\mathfrak {D}}^{2}}{8\pi }}=U_{0}$, so wird (2,10): ${\mathfrak {D}}={\mathfrak {E}}$ und (2,11) ${\mathfrak {H}}={\mathfrak {B}}$ und es gelten (2,12) die Gl. (2,4) des unkorrigierten Maxwellschen Vakuumfeldes, die nur in erster Näherung für kleine Feldstärken richtig sind. In nächster Näherung lautet nach (1,4) die Hamiltonfunktion

(2,13)

$U={\frac {{\mathfrak {B}}^{2}+{\mathfrak {D}}^{2}}{8\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}f({\mathfrak {BD}})=U_{0}+U_{1}$

worin $f$ eine Funktion 4. Grades in ${\mathfrak {B}}$ und ${\mathfrak {D}}$ ist.

Mit dem Relativitätsprinzip werden aber nur gewisse Zusätze $f$ im Einklang sein. Wir bestimmen diese, indem wir zeigen, daß sich die Feldgleichungen (2,1; 2,2; 2,12; 2,10; 2,11) auch aus einem Variationsprinzip herleiten lassen, und verlangen, daß die Lagrangefunktion $L$, die in diesem Variationsprinzip zum Extrem gemacht wird, eine Lorentzinvariante ist.

Dazu definieren wir im Anschluß an ein allgemeines Verfahren der Mechanik die Funktion

(2,14)

${\begin{array}{|c|}\hline \\{\dfrac {L}{4\pi }}={\dfrac {({\mathfrak {ED}})}{4\pi }}-U\\\\\hline \end{array}}$

und berechnen ihre partiellen Ableitungen nach ${\mathfrak {B}}$ und ${\mathfrak {E}}$: Wir finden (aus einer Änderung des Feldes um $\delta {\mathfrak {E}}$, $\delta {\mathfrak {B}}$, $\delta {\mathfrak {D}}$, $\delta {\mathfrak {H}}$):

${\frac {\delta L}{4\pi }}={\frac {\mathfrak {E}}{4\pi }}\delta {\mathfrak {D}}+{\frac {\mathfrak {D}}{4\pi }}\delta {\mathfrak {E}}-{\frac {\partial U({\mathfrak {BD}})}{\partial {\mathfrak {B}}}}\delta {\mathfrak {B}}-{\frac {\partial U({\mathfrak {BD}})}{\partial {\mathfrak {D}}}}\delta {\mathfrak {D}}$

oder nach (2,10):

${\frac {\delta L}{4\pi }}={\frac {\mathfrak {D}}{4\pi }}\delta {\mathfrak {E}}-{\frac {\partial U({\mathfrak {B,D}})}{\partial {\mathfrak {B}}}}\delta {\mathfrak {B}}$,

also:

(2,15)

${\begin{array}{|c|}\hline \\{\frac {\partial L({\mathfrak {B,E}})}{\partial {\mathfrak {E}}}}={\mathfrak {D}}\\\\\hline \end{array}}$

und wegen (2,11):

(2,16)

${\begin{array}{|c|}\hline \\{\frac {\partial L({\mathfrak {B,E}})}{\partial {\mathfrak {B}}}}=-{\mathfrak {H}}\\\\\hline \end{array}}$

und sehen, daß diese partiellen Ableitungen von $L$ durch Gl. (2,12) verknüpft sind zu einer Differentialgleichung für $L$

(2,17)

${\frac {1}{c}}{\frac {\partial }{\partial t}}{\frac {\partial L}{\partial {\mathfrak {E}}}}+\mathrm {rot} {\frac {\partial L}{\partial {\mathfrak {B}}}}=0$,

welche äquivalent ist mit dem Variationsprinzip:

(2,18)

${\begin{array}{|c|}\hline \\\iint L({\mathfrak {B,E}})dVdt=\mathrm {Extrem} \\\\\hline \end{array}}$

für die Lagrangefunktion $L=L({\mathfrak {B,E}})$ unter den Nebenbedingungen (2,1) oder (2,2). Die Lagrangeschen Gleichungen (2,1; 2,15; 2,16; 2,18), die ebenso wie die Hamiltonschen Gleichungen (2,1; 2,10; 2,11; 2,12) den Ablauf des Feldes bestimmen, sollen nun ihren Inhalt bekommen durch Aufstellung einer Lagrangefunktion $L=L({\mathfrak {B,E}})$, welche eine Lorentz- und Spiegelinvariante sein muß.

Alle Lorentzinvarianten des antisymmetrischen Tensors ${\mathfrak {B,E}}$ müssen Funktionen der beiden Lorentzinvarianten ${\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}$ und $({\mathfrak {B,E}})$ sein, von denen aber die zweite nicht spiegelinvariant ist.

Im niedrigsten zweiten Grade gibt es also nur die Lorentz- und Spiegelinvariante ${\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}$, die als Lagrangefunktion nach (2,15; 2,16; 2,18) zu den bekannten linearen Maxwellschen Vakuumgleichungen ${\mathfrak {D=E,H=B}}$ und (2,4) führt.

Im nächsthöheren vierten Grade können nur die Lorentz- und Spiegelinvarianten $\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right)^{2}$ und $({\mathfrak {EB}})^{2}$ gebildet werden. Also entspricht der allgemeinsten bis zur 4. Ordnung in den Feldstärken korrigierten Hamiltonfunktion (2,13) eine Lagrangefunktion

(2,19)

${\begin{array}{|c|}\hline \\{\frac {L}{4\pi }}={\frac {{\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}}{8\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[-\alpha \left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right)^{2}-\beta ({\mathfrak {EB}})^{2}\right]={\frac {L_{0}+L_{1}}{4\pi }}\\\\\hline \end{array}}$

Worin $-\alpha$ und $-\beta$ Zahlenkoeffizienten sind. Für diese Lagrangefunktion werden die Verknüpfungsgleichungen der Feldstärken ${\mathfrak {E}}$, ${\mathfrak {B}}$ mit den Größen ${\mathfrak {D}}$, ${\mathfrak {H}}$ (2,15; 2,16):

(2,20)

${\begin{array}{|c|}\hline \\{\begin{aligned}&{\frac {\mathfrak {D}}{4\pi }}={\frac {\mathfrak {E}}{4\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{{\mathfrak {E}}_{0}}^{2}}}\left[-4\alpha \left({\mathfrak {E}}^{2}-{\mathfrak {\dot {B}}}^{2}\right){\mathfrak {E}}^{2}-2\beta ({\mathfrak {BE}}){\mathfrak {B}}\right]\\&{\frac {\mathfrak {H}}{4\pi }}={\frac {\mathfrak {B}}{4\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[-4\alpha \left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {B}}+2\beta ({\mathfrak {BE}}){\mathfrak {E}}\right]\end{aligned}}\\\\\hline \end{array}}$

deren Umkehrung (bei konsequenter Vernachlässigung höherer als 4. Potenzen in den Feldstärken) lautet:

(2,20)

$\left\{{\begin{aligned}{\frac {\mathfrak {E}}{4\pi }}={\frac {\mathfrak {D}}{4\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[+4\alpha \left({\mathfrak {D}}^{2}-{\mathfrak {H}}^{2}\right){\mathfrak {D}}+2\beta ({\mathfrak {DH}}){\mathfrak {H}}\right]\\{\frac {\mathfrak {B}}{4\pi }}={\frac {\mathfrak {H}}{4\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[+4\alpha \left({\mathfrak {D}}^{2}-{\mathfrak {H}}^{2}\right){\mathfrak {H}}-2\beta ({\mathfrak {DH}}){\mathfrak {D}}\right.]\end{aligned}}\right.$

Zur Lagrangefunktion (2,19) gehört daher (2,14; 2,20) die Hamiltonfunktion:

(2,21)

${\begin{array}{|c|}\hline \\U={\frac {{\mathfrak {D}}^{2}-{\mathfrak {B}}^{2}}{8\pi }}+{\frac {\hbar c}{e^{2}}}{\frac {1}{E^{2}}}\left[\alpha \left({\mathfrak {D}}^{2}-{\mathfrak {B}}^{2}\right)^{2}+\beta ({\mathfrak {DB}})^{2}\right]=U_{0}+U_{1}\\\\\hline \end{array}}$

Damit ist die Wechselwirkungsenergie $U_{1}$ der Lichtquanten bis auf zwei numerische Konstanten $\alpha$ und $\beta$ bestimmt. Diese werden in § 8 durch Ausrechnung des Diracschen Matrixelements $H_{in}^{4}$ in zwei speziellen, möglichst einfachen Fällen und Vergleich mit (2,21) festgelegt werden.

§ 3. Diskussion der Vertauschungsrelationen für die Feldstärken im System der korrigierten Maxwellgleichungen

Die G1. (2,20) führten zu dem merkwürdigen Resultat, daß die elektrische Feldstärke ${\mathfrak {E}}$ und die zu den Potentialen $-{\tfrac {1}{4\pi c}}{\mathfrak {A}}$ konjugierte Größe ${\mathfrak {D}}$ (2,6) verschieden sind, während wir doch die allgemeine Theorie von Licht und Materie^[8] voraussetzten, in der sie gleich sind. Der darin liegende scheinbare Widerspruch erfordert eine ausführliche Diskussion. Es hat sich herausgestellt, daß der hier vorliegende physikalische Sachverhalt am besten klargemacht werden kann, wenn man das System: Strahlungs- und Materiefeld mit dem mechanischen System zweier Atome vergleicht. Wir führen diesen Vergleich durch, indem wir neben jede Eigenschaft des einen Systems die entsprechende des anderen Systems stellen:

Ein Licht- und Materiefeld kann beschrieben werden durch die Potentiale der Strahlung und die Dichte der Materie. Wenn keine wirklichen Elektronen anwesend sind und die Energie des Feldes nicht ausreicht, um Paare zu erzeugen, werden die Feldstärken zur Charakterisierung des Zustandes ausreichen.

Zwei Atome können beschrieben werden durch die Koordinaten ihrer Kerne und die Koordinaten ihrer Elektronen. Wenn vorausgesetzt wird, daß die Elektronen im Grundzustand sind, müssen die Koordinaten der Kerne allein zur Charakterisierung des Zustandes ausreichen.

Es können jedoch virtuell Paare erzeugt werden, die wieder zerstrahlen, und durch diese Übergänge entsteht eine Wechselwirkung zwischen den Lichtquanten.

Die Elektronen der beiden Atome können jedoch virtuell angeregt werden und wieder in den Grundzustand zurückkehren, und infolge dieser Übergänge wird es eine Wechselwirkung zwischen den Kernen geben: die van der Waalssche Anziehung.

Beschreibt man nun das Feld durch Gleichungen, die die Feldstärken allein enthalten, so muß man die Wechselwirkung zwischen den Lichtquanten, d. h. die nichtlineare Korrektur der Maxwellgleichungen, berücksichtigen.

Beschreibt man jetzt, etwa zur Berechnung der Bandenspektren des Moleküls, das System durch die Freiheitsgrade der Kerne allein, so müssen in ihren Bewegungsgleichungen die zusätzlichen van der Waalsschen Kräfte auftreten.

Der Zusatz $L_{1}$ zur Maxwellschen Lagrangefunktion $L_{0}$ enthält die magnetische Induktion ${\mathfrak {B}}$ und die elektrische Feldstärke ${\mathfrak {E}}$ (= Zeitableitung der Potentiale):

(3,19)

$\left\{{\begin{aligned}L=L_{0}({\mathfrak {EB}})+L_{1}({\mathfrak {EB}}),\\L_{0}=\int {\frac {\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right)}{2}}dV.\end{aligned}}\right.$

Der van der Waalssche Beitrag $L_{1}$ zur Lagrangefunktion hängt von den Koordinaten $q_{i}$ und bei genauer Berechnung, die wir hier voraussetzen wollen, auch von den Geschwindigkeiten ${\dot {q}}_{i}$ der Kerne ab:

${\begin{aligned}L=L_{0}\left(q_{i}{\dot {q}}_{i}\right)+L_{1}\left(q_{i}{\dot {q}}_{i}\right),\\L_{0}=\sum \limits _{i}{\frac {m}{2}}{\dot {q}}_{i}^{2}+\mathrm {Funkt} \left(q_{i}\right).\end{aligned}}$

Die zum Potential $-{\tfrac {1}{4\pi c}}{\mathfrak {A}}$ konjugierte Größe ${\mathfrak {D}}$ (2,6) ist daher nicht die elektrische Feldstärke, sondern es ist:

Die zu den Kernkoordinaten $q_{i}$ konjugierten Größen $p_{i}$ sind daher nicht die mit den Massen multiplizierten Geschwindigkeiten, sondern es ist:

(3,15 3,20)

$\left\{{\begin{aligned}&{\frac {\partial L}{\partial \left(-{\frac {\dot {\mathfrak {A}}}{4\pi c}}\right)}}={\mathfrak {D}}\\&={\mathfrak {E}}+{\frac {\partial L_{1}}{\partial \left(-{\frac {\dot {\mathfrak {A}}}{4\pi c}}\right)}};\ {\mathfrak {D\neq E}}.\end{aligned}}\right.$

${\begin{aligned}{\frac {\partial L}{\partial {\dot {q}}_{i}}}=&p_{i}=m{\dot {q}}_{i}+{\frac {\partial L_{i}}{\partial {\dot {q}}_{i}}};\\&p_{i}\neq {\dot {q}}_{i}m.\end{aligned}}$

Zwischen den Feldstärken bestehen daher jetzt nicht die gewöhnlichen Vertauschungsrelationen:

${\begin{aligned}{\mathfrak {E}}_{i}&(\xi ){\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi '){\mathfrak {E}}_{i}(\xi )\\&=2hci{\frac {\partial }{\partial \xi _{e}^{\prime }}}\delta (\xi -\xi '),\end{aligned}}$

sondern die abgeänderten:

(3,7)

$\left\{{\begin{aligned}{\mathfrak {D}}_{i}&(\xi ){\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi ')-{\mathfrak {D}}_{i}(\xi )\\&=2hci{\frac {\partial }{\partial \xi _{e}^{\prime }}}\delta (\xi -\xi ').\end{aligned}}\right.$

Zwischen den Koordinaten und Geschwindigkeiten der Kerne bestehen daher jetzt nicht die gewöhnlichen Vertauschungsrelationen:

$m{\dot {q}}_{i}q_{i}-q_{i}m{\dot {q}}_{i}={\frac {\hbar }{i}},$

sondern die abgeänderten:

$p_{i}q_{i}-q_{i}p_{i}={\frac {\hbar }{i}}.$

Im allgemeinen Fall jedoch, in dem das Strahlungsfeld auch Paare erzeugen kann, muß man das Gesamtfeld durch die Feldstärken und Materiedichten beschreiben, und die Wechselwirkung der Lichtquanten tritt nicht explizit in den Gleichungen auf: Die Lagrangefunktion enthält die Feldstärken nur in der Form:

$L=L_{0}({\mathfrak {EB}})+L'(\mathrm {Materie} ).$

Im allgemeinen Fall jedoch, in dem die Elektronen auch aus dem Grundzustand herauskönnen, muß man das System durch die Freiheitsgrade der Kerne und Elektronen beschreiben. Und die van der Waalsschen Kräfte treten nicht explizit in den Gleichungen auf: Die Lagrangefunktion enthält die Kernkoordinaten und Geschwindigkeiten nur in der Form:

$L=L_{0}\left(q_{i}{\dot {q}}_{i}\right)+L'(\mathrm {Elektronen} ).$

Dann ist aber wieder zu den Potentialen die elektrische Feldstärke konjugiert:

${\frac {\partial L}{\partial \left(-{\frac {\dot {\mathfrak {A}}}{4\pi c}}\right)}}={\mathfrak {D}}={\mathfrak {E}}$

und die Vertauschungsrelationen lauten:

${\begin{aligned}{\mathfrak {E}}_{i}&(\xi ){\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi '){\mathfrak {E}}_{i}(\xi )\\&=2hci{\frac {\partial }{\partial \xi _{e}^{\prime }}}\delta (\xi -\xi ')\end{aligned}}$

im Gegensatz zum Spezialfall (2,5).

Dann sind aber wieder zu den Kernkoordinaten die mit der Masse multiplizierten Geschwindigkeiten konjugiert:

${\frac {\partial L}{\partial {\dot {q}}_{i}}}=p_{i}=m{\dot {q}}_{i}$

und die Vertauschungsrelationen lauten:

$m{\dot {q}}_{i}q_{i}-q_{i}m{\dot {q}}_{i}={\frac {\hbar }{i}}$

im Gegensatz zum Spezialfall.)

Ebenso wie in der Lagrangeschen Mechanik können die oben beschriebenen Verhältnisse auch in der Hamiltonschen Mechanik ausgedrückt werden (wir bezeichnen mit $[ab]$ die Vertauschung: $ab-ba$).

Im allgemeinen enthält die Hamiltonfunktion $H$ des Feldes die Energie $H_{0}$ des Lichts und die Energie $H'$ der Materie. Die Feldpotentiale ${\mathfrak {A}}$ sind mit $H'$ vertauschbar und darum ist ${\mathfrak {E=D}}$:

${\begin{aligned}&H=H_{0}({\mathfrak {A}},{\mathfrak {D}})+H'(\mathrm {Materie} ),\\&H_{0}=\int {\frac {(\mathrm {rot} {\mathfrak {A}})^{2}+{\mathfrak {D}}^{2}}{8\pi }}dV,\end{aligned}}$

${\mathfrak {D}}$ zu ${\mathfrak {A}}$ konjugiert (2,6), ${\mathfrak {D}}$ und ${\mathfrak {A}}$ mit $H'$ vertauschbar,

${\begin{aligned}{\mathfrak {E}}&=-{\frac {1}{c}}{\mathfrak {\dot {A}}}=-{\frac {i}{c\hbar }}[H{\mathfrak {A}}]\\&=-{\frac {i}{c\hbar }}[H_{0}{\mathfrak {A}}]={\mathfrak {D}},\end{aligned}}$

also ${\mathfrak {E}}={\mathfrak {D}}$.

Im allgemeinen enthält die Hamiltonfunktion $H$ des Moleküls die Energie $H_{0}$ der Kerne und die Energie $H'$ der Elektronen. Die Kernkoordinaten $q_{i}$ sind mit $H'$ vertauschbar und darum ist $m{\dot {q}}_{i}=p_{i}$:

${\begin{aligned}H&=H_{0}\left(q_{i}p_{i}\right)+H'(\mathrm {Elektronen} ),\\&H_{0}=\sum \limits _{i}{\frac {p_{i}^{2}}{2m}}+\mathrm {Funkt} \left(q_{i}\right),\end{aligned}}$

$p_{i}$ zu $q_{i}$ konjugiert, $dhp_{i}q_{i}-q_{i}p_{i}={\tfrac {\hbar }{i}}$, $q_{i}$ vertauschbar mit $H'$,

${\begin{aligned}m{\dot {q}}_{i}&={\frac {mi}{\hbar }}\left[Hq_{i}\right]\\&={\frac {mi}{\hbar }}\left[H_{0}q_{i}\right]=p_{i},\end{aligned}}$

also $m{\dot {q}}_{i}=p_{i}$.

Im speziellen Fall aber, in dem keine wirkliche Materie erzeugt wird, kann die Energie der Elektronen durch eine Wechselwirkung der Lichtquanten $H_{1}({\mathfrak {AD}})$ ersetzt werden. Diese ist aber jetzt nicht mit den Feldpotentialen ${\mathfrak {A}}$ vertauschbar und daher ist ${\mathfrak {E\neq D}}$:

(2,22)

$H=H_{0}({\mathfrak {AD}})+H_{1}({\mathfrak {AD}})$,

${\mathfrak {D}}$ zu ${\mathfrak {A}}$ konjugiert (2,6),

(3,21)

$\left\{{\begin{aligned}{\mathfrak {E}}&=-{\frac {1}{c}}{\mathfrak {\dot {A}}}=-{\frac {i}{c\hbar }}[H{\mathfrak {A}}]\\&=-{\frac {i}{c\hbar }}[H_{0}{\mathfrak {A}}]\\&-{\frac {i}{c\hbar }}[H_{1}{\mathfrak {A}}]={\mathfrak {D}}+\dots ,\end{aligned}}\right.$

also ${\mathfrak {E\neq D}}$.

Im speziellen Fall aber, in dem die Atome nicht wirklich angeregt werden, kann die Energie der Elektronen durch die van der Waals-Kraft zwischen den Kernen $H_{1}\left(q_{i}p_{i}\right)$ ersetzt werden. Diese ist aber jetzt nicht mit den Kernkoordinaten vertauschbar und darum ist $m{\dot {q}}\neq p$:

$H=H_{0}\left(p_{i}q_{i}\right)+H_{1}\left(p_{i}q_{i}\right)$

$p_{i}$ zu $q_{i}$ konjugiert,

$dhp_{i}q_{i}-q_{i}p_{i}={\frac {\hbar }{i}}.$

${\begin{aligned}m{\dot {q}}_{i}&={\frac {mi}{\hbar }}\left[Hq\right]={\frac {mi}{\hbar }}\left[H_{0}q_{i}\right]\\&+{\frac {mi}{\hbar }}\left[H_{1}q_{i}\right]=p+\dots ,\end{aligned}}$

also $m{\dot {q}}\neq p$.

Dieser Vergleich macht es noch einmal deutlich, daß es sich bei der angeschriebenen Abänderung der Maxwellschen Gleichungen des Vakuums nicht um eine Abänderung der heutigen Feldtheorie^[9], sondern nur um einen speziellen Ausschnitt aus ihr handelt.

Außerdem betont er den folgenden Sachverhalt: Die Wechselwirkung zwischen den Lichtquanten und die Abänderung der Max wellgleichungen, die hier angegeben wurde, besteht nur solange wie keine wirklichen Paare erzeugt werden können, aber sie kommt nur dadurch zustande, daß virtuell doch Paare erzeugt werden. Ebenso kann man mit den van der Waalsschen Kräften nur so lange rechnen, wie die Atome im Grundzustand (oder doch in einem bestimmten Zustand) sind, obwohl die Kräfte nur dadurch zustande kommen, daß die Atome virtuell aus dem Grundzustand herausgehen.

Den mathematischen Prozeß der Änderung der Vertauschungsrelationen in einem mechanischen System bei Spezialisierung wird man sich so vorstellen, daß die hier vorgenommene Spezialisierung auf Fälle, in denen keine wirklichen Paare erzeugt werden können, eine Termauswahl im Gesamtsystem von Licht und Materie bedeutet, also eine Beschränkung aller Matrizen auf Teilmatrizen‚ ein Fortlassen gewisser Übergangs- und Besetzungsmöglichkeiten durch Streichen gewisser Matrixkästchen: Und die übrigbleibenden Teilmatrizen haben andere Vertauschungsrelationen als die ganzen.

${\begin{array}{|c|c|}\hline \color {white}\circ &\color {white}\circ \\\hline \color {white}\circ &\color {white}\circ \\\hline \end{array}}\rightarrow {\begin{array}{|c|c|}\hline \color {white}\circ &\circ \\\hline \circ &\circ \\\hline \end{array}}$

II. Teil

Nach diesen vorbereitenden Betrachtungen über die allgemeine Form des Resultats haben wir nun das Matrixelement $H_{in}^{4}$ der Diracschen Theorie für Streuung von Licht an Licht aufzustellen, zu zeigen, daß es mit dem entsprechenden Matrixelement einer Wechselwirkungsenergie von Licht mit Licht

(2,21)

${\bar {U}}_{1}={\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\int \left[\alpha \left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}+\beta ({\mathfrak {BD}})^{2}\right]dV$

identisch ist

$\left(g_{1}g_{2}\left|{\bar {U}}_{1}\right|-g_{3}-g_{4}\right)=H_{in}^{4}$,

und es schließlich in zwei einfachen Spezialfällen auszurechnen, welche die Bestimmung der beiden Konstanten $\alpha$, </math>\beta</math> in ${\bar {U}}_{1}$ statten. Wir beginnen mit der ausführlichen Darstellung des Störungsschemas, welches zu diesen Rechnungen verwandt werden soll.

§ 4. Allgemeines Störungsschema, das zur Berechnung der Streuung von Licht an Licht verwandt wird

In einem abgeschlossenen System mit den annähernd stationären Zuständen $i$, $k$, $l$, $m$, $n$, $\mu$, $\mu '$, die die Energien $E_{i}$, $E_{k}$, $\dots$ und die Besetzungswahrscheinlichkeiten $\left|a_{i}\right|^{2}$, $\left|a_{k}\right|^{2}$, $\dots$ haben, ruft eine Störung mit der zeitunabhängigen Energiematrix $V_{ik}$ die Zustandsänderungen:

(4,1)

$i\hbar {\frac {\partial }{\partial t}}{a_{\mu }}^{\prime }(t)=\sum \limits _{\mu }e^{{\frac {i}{h}}(E\mu '-E\mu )t}V_{\mu \mu '}a_{\mu }(t)$

hervor. ($t$: Zeit, $h=2\pi \hbar$: Plancksches Wirkungsquantum). Entwickelt man die Störung $V$ und die Zustände $a_{\mu }$ nach einem kleinen Parameter:

(4,2)

$\left\{{\begin{aligned}V&=\qquad V^{1}+V^{2}+V^{3}+V^{4}+\dots \\a_{\mu }&={a_{\mu }}^{0}+{a_{\mu }}^{1}+{a_{\mu }}^{2}+{a_{\mu }}^{3}+{a_{\mu }}^{4}+\dots ,\end{aligned}}\right.$

und setzt voraus, daß zu Anfang der Zustand $i$ verwirklicht sei $\left({a_{\mu }}^{0}(t)=\delta _{i\mu },\ {a_{\mu }}^{\alpha }(0)=0\ {\mbox{für}}\ \alpha \geqslant 1\right)$, so folgt in 1. Näherung:

$i\hbar {\frac {\partial }{\partial t}}{a_{k}}^{1}(t)=\sum \limits _{\mu }e^{{\frac {i}{\hbar }}(E_{k}-E_{\mu })t}V_{\mu k}{a_{\mu }}^{0}(t)=e^{{\frac {i}{\hbar }}(E_{k}-E_{i})t}V_{ik}$,

integriert:

(4,3)

${a_{k}}^{1}(t)=\left({\frac {e^{{\frac {i}{\hbar }}(E_{k}-E_{i})t}-1}{E_{i}-E_{k}}}\right)\cdot V_{ik}$

Der zweite Faktor dieser Näherung ist das Matrixelement der Störung $V^{1}$ für den Übergang $i\rightarrow k$. Der erste Faktor ist nur beträchtlich innerhalb des Ungenauigkeitsbereichs $\left|E_{k}-E_{i}\right|\lesssim {\frac {h}{t}}$. D. h. für kleine $t$ ist $a^{1}(t)$ immer von Bedeutung, für große $t$ aber nur, falls das System unter Energieerhaltung $E_{i}=E_{k}$ vom Zustande $i$ in den Zustand $k$ übergehen kann.

Eine Übergangswahrscheinlichkeit $i\rightarrow k$ erster Ordnung

$\left(\left|a^{1}(t)\right|^{2}\neq 0\ {\mbox{für große}}\ t\right)$

besteht also nur, wenn $V_{ik}\neq 0$ und $E_{i}=E_{k}$ ist.

Wenn diese Bedingungen erfüllt sind, berechnet man in bekannter Weise nach Dirac die gesamte Übergangswahrscheinlichkeit $i\rightarrow k$ zu:

(4,4)

${\frac {1}{t}}\sum \limits _{k'\sim k}\left|a_{k'}(t)\right|^{2}\approx {\frac {1}{t}}\left|V_{ik}^{1}\right|^{2}\cdot {\frac {1}{\Delta E}}\cdot \int \limits _{-\infty }^{+\infty }2{\frac {1-\cos \left(E_{k'}-E_{i}\right){\frac {t}{\hbar }}}{\left(E_{i}-E_{k'}\right)^{2}}}dE_{k'}={\frac {2\pi }{\hbar }}\cdot {\frac {1}{\Delta E}}\cdot \left|V_{ik}^{1}\right|^{2}$,

worin $1/\Delta E$ die Termdichte im Energiespektrum des Systems beim Endzustand $k$ bedeutet.

Wenn es aber in erster Ordnung keine Übergangswahrscheinlichkeit gibt, muß man höhere Näherungen betrachten. Wir nehmen jetzt an, daß bis zur $(\beta -1)$ten Ordnung alle Übergangswahrscheinlichkeiten (von jedem Zustand $i$ zu jedem anderen Zustand gleicher Energie) verschwinden und daß es zuerst in $\beta$ter Näherung Übergänge geben kann, daß also

(4,5)

$\left|a_{\mu }^{1}(t)\right|^{2}=\left|a_{\mu }^{2}(t)\right|^{2}=\left|a_{\mu }^{3}(t)\right|^{2}=\dots =\left|a_{\mu }^{\beta -1}(t)\right|^{2}=0,\ \left|a_{\mu }^{\beta }(t)\right|^{2}\neq 0$

für große $t$ und alle $\mu \neq i$, wenn $E_{\mu }=E_{i}$.

Unter dieser Voraussetzung stellen wir die Behauptung auf: Alle Näherungen bis einschließlich zur $\beta$ten haben die Zeitabhängigkeit:

(4,6)

$\left\{{\begin{aligned}&a_{\mu (t)}^{\alpha '}=\left({\frac {e^{{\frac {i}{\hbar }}(E_{\mu }-E_{i})t}-1}{E_{i}-E_{\mu }}}\right)\cdot H_{i\mu }^{\alpha '}+\sum \limits _{\varkappa \neq i}\left({\frac {e^{{\frac {i}{\hbar }}(E_{\mu }-E_{\varkappa })t}-1}{E_{\varkappa }-E_{\mu }}}\right)\cdot K_{\varkappa \mu }^{\alpha '}\\&\qquad \qquad {\mbox{für}}\ \alpha '=1,2,\dots \beta -1,\beta .\end{aligned}}\right.$

Darin bedeutet:

$i$ den Index des Anfangszustandes,

$\mu$ den Index des betrachteten Zustandes,

$\varkappa$ den Index eines von $i$ und $\mu$ verschiedenen „Zwischen“zustandes.

Der erste Summand führt vom Anfangszustand $i$ nach dem betrachteten Zustand $\mu$, d. h. sein Zeitfaktor ist bei großem $t$ nur für $E_{i}=E_{\mu }$ groß.

Der zweite Summand führt von einem vom Anfangszustand verschiedenen Zustand $\varkappa \neq i$ zum betrachteten Zustand $\mu$, d. h. sein Zeitfaktor wiegt bei großem $t$ nur für $E_{\varkappa }=E_{\mu }$.

$H_{i\mu }^{\alpha '}$ und $K_{\varkappa \mu }^{\alpha '}$ sollen die Zeit $t$ nicht enthalten.

Beweis: Für die erste Ordnung ist die Behauptung schon durch (4,3) erwiesen und zwar ist

(4,7)

${\begin{array}{|c|}\hline H_{i\mu }^{1}=V_{i\mu }^{1}\\\hline \end{array}},\ K_{\varkappa \mu }^{1}=0$.

Wir nehmen nun an, daß die Behauptung für alle Lösungen bis einschließlich zur $(\alpha -1)$ten_bewiesen sei

$\left(\alpha '=1,2,\cdots (\alpha -1);\ \alpha -1<\beta \right)$,

und zeigen, daß sie dann auch für die $\alpha$te richtig ist $(\alpha '=\alpha \leqslant \beta )$. Die $\alpha$te Näherung wird (wenn wir zu Anfang den Zustand $i$ verwirklicht denken und als vorläufigen Abschluß den Zustand $\mu '$ betrachten:

(4,8)

$i\hbar {\frac {\partial }{\partial t}}a_{\mu '}^{\alpha }(t)=\sum \limits _{\mu }e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\mu })t}\cdot \left[a_{i\mu }^{\alpha -1}V_{\mu \mu '}^{1}+\cdots +a_{i\mu }^{1}V_{\mu \mu '}^{\alpha -1}+a_{i\mu }^{0}V_{\mu \mu '}^{\alpha }\right]$

und mit (4,6):

(4,8')

$=e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{i})t}\cdot \left[\sum \limits _{\mu }{\frac {H_{i\mu }^{\alpha -1}V_{\mu \mu '}^{1}}{E_{i}-E_{\mu }}}+\cdots +\sum \limits _{\mu }{\frac {H_{i\mu }^{1}V_{\mu \mu '}^{\alpha -1}}{E_{i}-E_{\mu }}}+V_{\mu \mu '}^{\alpha }\right]+\sum \limits _{\varkappa '\neq i}e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\varkappa '})}\cdot K_{\varkappa '\mu }^{\alpha }$.

Darin faßt der erste Teil alle Glieder zusammen, deren Zeitfaktor im Exponent die Energiedifferenz $E_{i}-E_{\mu '}$ vom Anfangszustand und dem betrachteten vorläufigen Endzustand $\mu '$ hat (und die durch Einsetzen des ersten Teils vom ersten Summanden (4,6) in (4,8) entstehen). Und der zweite Teil faßt alle Glieder zusammen, die diese Eigenschaft nicht haben, und die ausführlich lauten würden:

(4,9)

$\left\{{\begin{aligned}\sum \limits _{\varkappa '\neq i}e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\varkappa '})t}\cdot K_{\varkappa \mu '}^{\alpha }&=-\sum \limits _{\mu }e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\mu })t}\cdot \left[{\frac {H_{i\mu }^{\alpha -1}V_{\mu \mu '}^{1}}{E_{i}-E_{\mu }}}+\cdots +{\frac {H_{i\mu }^{1}V_{\mu \mu '}^{\alpha -1}}{E_{i}-E_{\mu }}}\right]\\&+\sum \limits _{\begin{array}{c}\mu \neq i\\\varkappa \neq i\end{array}}\left(e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\varkappa })t}-e^{{\frac {i}{\hbar }}(E_{\mu '}-E_{\mu })t}\right)\cdot \left[{\frac {K_{\varkappa \mu }^{\alpha -1}V_{\mu \mu '}^{1}}{E_{\varkappa }-E_{\mu }}}+\cdots +{\frac {H_{\varkappa \mu }^{2}V_{\mu \mu '}^{\alpha -2}}{E_{\varkappa }-E_{\mu }}}\right]\end{aligned}}\right.$.

Zeitintegration von (4,8) ergibt für die $\alpha$te Näherung einen Ausdruck der Form (4,6), wenn man

(4,10)

${\begin{array}{|c|}\hline H_{i\mu '}^{\alpha }=\sum \limits _{\mu }{\frac {H_{i\mu }^{\alpha -1}V_{\mu \mu '}^{1}}{E_{i}-E_{\mu }}}+\cdots +\sum \limits _{\mu }{\frac {H_{i\mu }^{1}V_{\mu \mu '}^{\alpha -1}}{E_{i}-E_{\mu }}}+V_{i\mu '}^{\alpha }\\\hline \end{array}}$

setzt, womit die Behauptung bewiesen ist.

Nach Voraussetzung (4,5) sind nun der erste und der zweite Summand von (4,6) in allen Näherungen bis einschließlich zur $(\beta -1)$ten klein für große $t$

(4,6)

$\left\{{\begin{aligned}{\mbox{d. h.}}&E_{\mu }\neq E_{i}&{\mbox{falls}}&H_{i\mu }^{\alpha }\neq 0\\{\mbox{und}}&E_{\mu }\neq E_{\varkappa }&{\mbox{falls}}&K_{\varkappa \mu }^{\alpha }\neq 0\end{aligned}}\right\}\ {\mbox{für}}\ \alpha '=1,2,\dots \beta -1$.

Ferner ist der zweite Summand (4,6) der $\beta$ten Näherung klein für große $t$ (d. h. $E_{\mu }\neq E_{\varkappa }$ falls $K_{\mu \varkappa }^{\beta }\neq 0$). Denn anderenfalls hätte es, wie man aus (4,9) ersieht, schon in früherer als $\beta$ter Näherung einen Übergang $\varkappa \rightarrow \mu '$ gegeben gegen die Voraussetzung. Aus demselben Grund sind alle in (4,10) vorkommenden Nenner $\neq 0$.

Da aber in $\beta$ter Näherung eine Übergangswahrscheinlichkeit $i\rightarrow \mu '$ bestehen soll, muß diese vom ersten Summanden (4,6) herrühren, also durch

$\left|a_{i\mu '}^{\beta }(t)\right|^{2}=\left|H_{i\mu '}^{\beta }\right|^{2}2{\frac {1-\cos \left(E_{\mu '}-E_{i}\right){\frac {t}{\hbar }}}{\left(E_{i}=E_{\mu '}\right)^{2}}}$

bestimmt sein, woraus nach der obigen Diracschen Schlußweise (4,4) die Übergangswahrscheinlichkeit folgt:

(4,11)

${\begin{array}{|c|}\hline {\frac {2\pi }{\hbar }}{\frac {1}{\Delta E}}\cdot \left|H_{i\mu '}^{\beta }\right|^{2}\\\hline \end{array}}$

(4,11), (4,10) und (4,7) enthalten das Resultat der Störungsrechnung: Die Übergangswahrscheinlichkeit in der kleinsten nichtverschwindenden ($\beta$ten) Ordnung ist Produkt aus der (mit $2\pi /\hbar$ multiplizierten) Zahl der Zustände $1/\Delta E$ pro Energieintervall beim Endzustand und dem Quadrat eines „Matrixelements“.

Das Matrixelement $\beta$ter Ordnung (4,10) $H_{i\mu '}^{\beta }$, welches vom Anfangszustand $i$ zum Endzustand $\mu '$ führt, ist zusammengesetzt aus den Matrixelementen $V_{ik}^{\beta '\leqslant \beta }$ der Störungsenergie; z. B.

(4,12)

$H_{in}^{4}={\frac {V_{ik}^{1}V_{ke}^{1}V_{em}^{1}V_{mn}^{1}}{\left(E_{i}-E_{k}\right)\left(E_{i}-E_{e}\right)\left(E_{i}-E_{m}\right)}}+\cdots +V_{in}^{4}$[10].

Hierbei können einige Teile der Störungsenergie $\left(V^{4}\right)$ direkt in erster Ordnung vom Anfangszustand ($i$) zum Endzustand ($n$) führen, andere Störungen $\left(V^{1}\right)$ dagegen nur durch Teilprozesse

$(i\rightarrow k,\ k\rightarrow l,\ l\rightarrow m,\ m\rightarrow n)$

über Zwischenzustände ($k$, $l$, $m$) in höherer (4ter) Ordnung. Diese Teilprozesse zu den „virtuellen“ Zwischenzuständen verlangen keine Energieerhaltung wie der Gesamtprozeß $(i\rightarrow n)$ zum wirklichen Endzustand. Obwohl also die Zustande $k$, $l$, $m$ wegen des Energiesatzes gar nicht wirklich vom System angenommen werden können (sonst hatte es schon in früherer Näherung Übergänge gegeben, welche der hier angegebenen Formel die Voraussetzung entziehen würden), bewirkt doch ihre virtuelle Möglichkeit den betrachteten Übergang $i\rightarrow n$. Auf diesem Umstand beruht die Streuung von Licht an Licht.

§ 5. Aufstellung der Matrix $H_{in}^{4}$ der Diracschen Theorie für Streuung von Licht an Licht

Wir wenden dieses Störungsschema an auf das System: Strahlungs- und Materiefeld. Als seine annähernd stationären Zustände wählen wir ebene Licht- und Materiewellen. Die Störungsenergie besteht dann aus der Koppelung zwischen Licht und Materie und gewissen Subtraktionsgliedern, die nach Heisenberg^[11] mit der Hamiltonfunktion der gewöhnlichen Löchertheorie kombiniert werden müssen, um endliche und mit den Erhaltungssätzen verträgliche Resultate zu ergeben.

Im folgenden bezeichnet:

(5,1)

$\left\{{\begin{aligned}{\mathfrak {A}}&&&{\text{das Vektorpotential des Strahlungsfeldes,}}\\\psi (\xi ,s),\ (s=1,2,3,4)&&&{\text{die Wellenfunktion des Materiefeldes,}}\\\alpha =\alpha _{s\varrho '}&&&{\text{den Diracoperator,}}\\\xi ,\mathrm {d} V&&&{\text{Ort und Volumenelement im Strahlungsfeld,}}\\V&&&{\text{das Volumen eines Wuerfels, in dem das Feld als periodisch angenommen wird,}}\\{\mathfrak {g,e}}&&&{\text{Impuls und Polarisation eines Lichtquants,}}\\{\mathfrak {p}},\sigma \rightarrow \pm 1,\lambda \rightarrow \pm 1&&&{\text{Impuls, Spin und Energievorzeichen eines Elektrons,}}\\d{\mathfrak {p}}&&&{\text{das Impulsraumelement,}}\\M_{g{\mathfrak {e}}},B_{g{\mathfrak {e}}}&&&{\text{Besetzungszahl und Amplitude der ebenen Lichtwelle}}\ g,\ {\mathfrak {e}},\\N_{{\mathfrak {p}}\sigma \lambda },A_{{\mathfrak {p}}\sigma \lambda }&&&{\text{ Besetzungszahl und Amplitude der ebenen Materiewelle}}\ {\mathfrak {p}},\lambda ,\sigma ,\\c,h=2\pi h&&&{\text{Lichtgeschwindigkeit und Plancksches Wirkungsquantum,}}\\e,m&&&{\text{Elektronen-Ladung und -Masse}}\end{aligned}}\right.$.

Die Zerlegung des Feldes nach ebenen Wellen ist:

(5,2)

$\left\{{\begin{aligned}{\mathfrak {A}}=&\sum \limits _{g{\mathfrak {e}}}{\mathfrak {A}}_{g}\left(B_{g{\mathfrak {e}}}+B_{-g{\mathfrak {e}}}^{\ast }\right),\quad {\mathfrak {A}}_{g}={\mathfrak {e}}{\sqrt {\frac {ch\hbar }{|g|V}}}e^{{\frac {i}{\hbar }}({\mathfrak {g}}\xi )},\\\psi =&\sum \limits _{{\mathfrak {p}}\lambda \sigma }{\frac {e^{{\frac {i}{\hbar }}({\mathfrak {g}}\xi )}}{\sqrt {V}}}\cdot a_{{\mathfrak {p}}\lambda \sigma }(s)\cdot A_{{\mathfrak {p}}\lambda \sigma },\quad ({\mathfrak {ee}})=1,\ ({\mathfrak {eg}})=0\\&\sum \limits _{s=1}^{4}\left|a_{{\mathfrak {p}}\lambda \sigma }(s)\right|^{2}=1.\end{aligned}}\right.$

Die Potentiale und Dichten sind Operatoren, charakterisiert durch die Matrixeigenschaften ihrer Fourieramplituden:

$B_{g}^{\ast }$ bzw. $B_{g}$ bedeutet das Entstehen bzw. Verschwinden eines Lichtquants, $A_{\mathfrak {p}}^{\ast }$ bzw. $A_{\mathfrak {p}}$ bedeutet das Entstehen bzw. Verschwinden eines Elektrons, d. h. das Matrixelement von $B_{g}^{\ast }$ ist $\neq 0$ nur für einen Übergang, bei dem ein Lichtquant ${\mathfrak {g}}$ entsteht:

(5,3)

$\left\{{\begin{aligned}\left(\cdots M_{g}\cdots \left|B_{g}^{\ast }\right|\cdots M_{g}+1\cdots \right)&={\sqrt {M_{g}+1}},\\\left(\cdots M_{g}\cdots \left|B_{g}\right|\cdots M_{g}-1\cdots \right)&={\sqrt {M_{g}}},\\\left(\cdots N_{\mathfrak {p}}\cdots \left|A_{\mathfrak {p}}^{\ast }\right|\cdots N_{\mathfrak {p}}+1\cdots \right)&={\sqrt {1-N_{\mathfrak {p}}}}\cdot J\\\left(\cdots N_{\mathfrak {p}}\cdots \left|A_{\mathfrak {p}}\right|\cdots N_{\mathfrak {p}}-1\cdots \right)&={\sqrt {N_{\mathfrak {p}}}}\cdot J\end{aligned}}\right.$

mit der Jordan-Wignerschen Vorzeichenfunktion:

$J=(-1)^{\sum \limits ^{{\mathfrak {p}}\lambda }N{\mathfrak {p}}'\lambda '}$

Ein Prozeß der Streuung von Licht an Licht wird beschrieben durch:

(5,4)

$\left\{{\begin{array}{l}\qquad {\mathfrak {g}}^{1},{\mathfrak {g}}^{2},\ g^{1}=\left|{\mathfrak {g}}^{1}\right|,\ g^{2}=\left|{\mathfrak {g}}^{2}\right|,\\{\mbox{die Impulse und Energien der beiden primären, absorbierten}}\\{\mbox{Lichtquanten;}}\\\qquad -{\mathfrak {g}}^{3},-{\mathfrak {g}}^{4},\ -g^{3}=\left|{\mathfrak {g}}^{3}\right|,\ -g^{4}=\left|{\mathfrak {g}}^{4}\right|,\\{\mbox{die Impulse und Energien der beiden sekundaeren, emit-}}\\{\mbox{tierten Lichtquanten;}}\\\qquad {\mathfrak {e}}^{1},{\mathfrak {e}}^{2},{\mathfrak {e}}^{3},{\mathfrak {e}}^{4},\ \left(\left|{\mathfrak {e}}^{1}\right|=1;\ {\mathfrak {e}}^{1}\bot {\mathfrak {g}}^{1}\cdots \right)\\{\mbox{die dazugehörigen Polarisationen;}}\\\qquad \left(g^{1},g^{2}|0|-g^{3},-g^{4}\right)\\{\mbox{das Matrixelement eines Operators O für Streuung von Licht}}\\{\mbox{an Licht, d. h, für den Übergang zweier Lichtquanten}}\ g^{1},g^{2}\\{\mbox{in zwei andere}}-g^{3},-g^{4}\ {\text{(statt der ausführlichen Bezeichnung:}}\\\qquad \left[\cdots N_{g^{1}}N_{g^{2}}\cdots N_{-g^{3}}N_{-g^{4}}\cdots |0|\cdots N_{g^{1}}-1,N_{g^{2}}-1,\right.\\\qquad \left.\cdots N_{-g^{3}}+1,N_{-g^{4}}+1\cdots \right]).\end{array}}\right.$

Die Störungsenergie des nach ebenen Wellen approximierten Feldes enthält, entwickelt nach Potenzen der Elektronenladung $e$:

Die Koppelung von Licht und Materie, die Strom und durch Potential bestimmt ist:

(5,5)

$V^{1}=e\int \psi ^{\ast }(\alpha {\mathfrak {A}})\psi dV$

und die Subtraktionsglieder^[12]:

(5,6)

$\left\{{\begin{aligned}&V^{2}=e^{2}\int dV\ {\mbox{(Funktion zweiter Ordnung in den Feldstärken)}}\\&V^{3}=e^{3}\int dV\ {\mbox{(Funktion dritter Ordnung in den Feldstärken)}}\\&V^{4}=e^{4}\left(-{\frac {1}{12\pi ^{2}}}\right)\left({\frac {1}{\hbar c}}\right)^{3}\lim \limits _{{\mathfrak {r}}\rightarrow 0}\int {\frac {({\mathfrak {A}}(\xi ){\mathfrak {r}})^{4}}{|{\mathfrak {r}}|^{4}}}dV.\end{aligned}}\right.$

$V^{1}$ ist erster Ordnung in den Potentialen, zweiter Ordnung in den Materiewellen und gibt daher (5,3) zu Übergängen Anlaß, bei denen ein Lichtquant $g$ entsteht (oder vergeht) und ein Elektron ${\mathfrak {p}}$ von einem Zustand in einen anderen ${\mathfrak {p}}'$ springt. Das Matrixelement von $V_{1}$ für diesen Übergang ist (5,2, 5,3):

(5,7)

$V_{ik}=e\int {\mathfrak {A}}_{\mp {\mathfrak {g}}}\left({\overset {\lambda \sigma }{\mathfrak {p}}}|\alpha |{\overset {\lambda '\sigma '}{{\mathfrak {p}}'}}\right){\frac {e^{{\frac {i}{\hbar }}({\mathfrak {p}}-{\mathfrak {p}}')\xi }}{V}}dV$,

(5,8)

$=e{\sqrt {\frac {ch\hbar }{|g|V}}}\left({\overset {\lambda \sigma }{\mathfrak {p}}}|\alpha {\mathfrak {e}}|{\overset {\lambda '\sigma '}{{\mathfrak {p}}'}}\right)$

falls der Impuls beim Übergang erhalten bleibt $({\mathfrak {p}}-{\mathfrak {p}}'=\pm {\mathfrak {g}})$‚ 0 falls er nicht erhalten bleibt.

Darin bezeichnet $\left({\overset {\lambda \sigma }{\mathfrak {p}}}|\alpha {\mathfrak {e}}|{\overset {\lambda '\sigma '}{{\mathfrak {p}}'}}\right)$ das Matrixelement der 4reihigen Diracmatrix $(\alpha {\mathfrak {e}})$ für das Zustandspaar ${\overset {\lambda \sigma }{\mathfrak {p}}}$ und ${\overset {\lambda '\sigma '}{{\mathfrak {p}}'}}$ eines Elektrons. Die Faktoren ${\sqrt {M_{g}+1}}$ und ${\sqrt {M_{g}}}$ sind hier und im folgenden der Kürze halber weggelassen.

$V^{2}$ bzw. $V^{3}$ sind zweiter bzw. dritter Ordnung in den Feldstärken und führen daher zu Matrixelementen, welche zwei bzw. drei Lichtquanten der Impulssumme 0 kombinieren.

$V^{4}$ endlich enthält die Potentiale in vierter Ordnung und kann daher zwei Lichtquanten $+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}$ in zwei andere der gleichen Impulssumme $-{\mathfrak {g}}^{3}-{\mathfrak {g}}^{4}$ überführen. Sein Matrixelement für diesen Übergang ist (5,2, 5,3):

(5,9)

$\left(g^{1}g^{2}\left|V^{4}\right|-g^{3}-g^{4}\right)={\frac {64\pi }{3}}C\lim \limits _{{\mathfrak {r}}\rightarrow 0}\sum \limits _{\mathrm {Perm} }{\frac {\left({\mathfrak {e}}^{1}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{2}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{3}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{4}{\mathfrak {r}}\right)}{|{\mathfrak {r}}|^{4}}}=V_{in}^{4}$.

Darin bezeichnet $\sum \limits _{\mathrm {Perm} }$ die Summe über alle 24 Permutationen der Indizes 1, 2, 3, 4 in den Vektoren ${\mathfrak {e}}^{1}$, ${\mathfrak {e}}^{2}$, ${\mathfrak {e}}^{3}$, ${\mathfrak {e}}^{4}$, und es ist:

(5,10)

$C=-{\frac {1}{32\cdot (2\pi )^{3}}}\left({\frac {e^{2}}{\hbar c}}\right)^{2}{\frac {1}{\hbar c}}\left({\frac {ch\hbar }{V}}\right)^{2}{\frac {V}{\sqrt {g^{1}g^{2}g^{3}g^{4}}}}$.

Zur Streuung von Licht an Licht kann also $V_{1}$ nur in 4ter, $V_{4}$ aber in 1ter Ordnung führen. Die anderen Glieder $V_{2}$ und $V_{3}$ geben keinen Beitrag. (Denn $V_{3}$ müßte mit $V_{1}$ zusammengesetzt werden, was einen Elektronensprung verlangen würde, $V_{2}$ aber mit zwei Gliedern $V_{1}$ oder mit sieh selbst, was den verwandelten Lichtquanten spezielle Bedingungen auferlegen würde.)

D. h.: die Streuung von Licht an Licht ist ein Prozeß 4ter Ordnung in der Diracschen Theorie. Sein Matrixelement wird aus der gewöhnlichen Störung $V_{1}$ in 4ter Ordnung und dem Heisenbergschen Subtraktionsglied $V_{4}$ in 1ter Ordnung zusammengesetzt: (4,12)

(5,11)

$H_{in}^{4}=\sum \limits _{kem}{\frac {V_{ik}^{1}V_{ke}^{1}V_{em}^{1}V_{mn}^{1}}{\left(E_{i}-E_{k}\right)\left(E_{i}-E_{e}\right)\left(E_{i}-E_{m}\right)}}+V_{in}^{4}$

Dabei besteht Impulserhaltung für die Teilprozesse $(i\rightarrow k,\ k\rightarrow c,\ e\rightarrow m,\ m\rightarrow n)$ und damit für den ganzen Prozeß, Energieerhaltung dagegen nur für den Gesamtprozeß $(i\rightarrow n)$:

(5,11')

$\left\{{\begin{aligned}{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}+{\mathfrak {g}}^{3}+{\mathfrak {g}}^{4}&=0\\g^{1}+g^{2}+g^{3}+g^{4}&=0.\end{aligned}}\right.$

Die Teilprozesse, über welche die Koppelung $V^{1}$ zur Streuung von Licht an Licht führt, sind:

${\begin{array}{c|c|c|c|c}\hline \hline {\textrm {Licht-}}&&&\\{\textrm {quanten}}&{\textrm {Absorption}}&{\textrm {Absorption}}&{\textrm {Emission}}&{\textrm {Emission}}\\{\begin{array}{c|}\hline {\textrm {Elek-}}\\{\textrm {tronen}}\end{array}}&{\textrm {von}}\ g^{1}&{\textrm {von}}\ g^{2}&{\textrm {von}}-g^{3}&{\textrm {von}}-g^{4}\\\hline \hline &&&\\\mu =1&{\textrm {Paarerzeugung}}&{\textrm {Elektronensprung}}&{\textrm {Elektronensprung}}&{\textrm {Paarvernichtung}}\\\mu =2&{\textrm {Paarerzeugung}}&{\textrm {Elektronensprung}}&{\textrm {Positronensprung}}&{\textrm {Paarvernichtung}}\\\mu =3&{\textrm {Paarerzeugung}}&{\textrm {Positronensprung}}&{\textrm {Elektronensprung}}&{\textrm {Paarvernichtung}}\\\mu =4&{\textrm {Paarerzeugung}}&{\textrm {Positronensprung}}&{\textrm {Positronensprung}}&{\textrm {Paarvernichtung}}\\\mu =5&{\textrm {Paarerzeugung}}&{\textrm {Paarerzeugung}}&{\textrm {Zerstrahlungdes}}&{\textrm {Zerstrahlungdes}}\\&&&\ {\textrm {Elektronsvom}}&\ {\textrm {Positronsvom}}\\&&&\ {\textrm {1.mitdemPosi-}}&\ {\textrm {1.mitdemElek-}}\\&&&\ {\textrm {tronvom2.Paar}}&\ {\textrm {tronvom2.Paar}}\\\mu =6&{\textrm {Paarerzeugung}}&{\textrm {Paarerzeugung}}&{\textrm {Zerstrahlungdes}}&{\textrm {Zerstrahlungdes}}\\&&&\ {\textrm {Positronsvom}}&\ {\textrm {Elektronsvom}}\\&&&\ {\textrm {1.mitdemElek-}}&\ {\textrm {1.mitdemPosi-}}\\&&&\ {\textrm {tronvom2.Paar}}&\ {\textrm {tronvom2.Paar}}\end{array}}$

Fig. 1. Die 6 Übergangsmöglichkeiten

Hierbei kann die erste Paarerzeugung statt unter Absorption von $g^{1}$, wie in der Figur (und als Repräsentant in den folgenden Rechnungen) angegeben, auch unter Emission von $-g^{3}$ vor sich gehen usw. D. h. es können die 4 Überschriften, die über den Spalten der Tabelle in deren oberster Zeile stehen (und in allen folgenden Formeln die 4 Lichtquantenindizes 1, 2, 3, 4) noch in beliebiger Weise permutiert werden unter Beibehaltung aller übrigen Tabellen- (und Formel-) Teile.

Je nach dem Verhalten der erzeugten Paare gibt es 6 verschiedene Übergangswege, bezeichnet durch $\mu =1$ bis 6 und jeder dieser 6 Übergänge kann mit allen 24 Permutationen der Lichtquanten kombiniert werden.

Im folgenden bezeichnet (vgl. Figur):

(5,12)

$\left\{{\begin{aligned}&{\mathfrak {p}}^{4}={\mathfrak {p}}\ {\mbox{den (negativen) Impuls des zuerst erzeugten Positrons,}}\\&p=|{\mathfrak {p}}|\ {\mbox{seinen Betrag,}}\\&\left.{\begin{array}{r}{\mathfrak {p}}^{1}={\mathfrak {p}}+{\mathfrak {g}}^{1}\\{\mathfrak {p}}^{2}={\mathfrak {p}}+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\\{\mathfrak {p}}^{3}={\mathfrak {p}}+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}+{\mathfrak {g}}^{3}={\mathfrak {p}}-{\mathfrak {g}}^{4}\end{array}}\right\}{\begin{array}{l}{\mbox{die Impulse der Elektronen}}\\{\mbox{in den Zwischenzuständen}},\end{array}}\\&\left.{\begin{array}{c}p_{0}^{i}=+{\sqrt {(mc)^{2}+\left({\mathfrak {p}}^{i}{\mathfrak {p}}^{i}\right)}}_{(i=1\dots 4)}\\{\textrm {z.b.}}:{p_{0}}^{1}=\left({\mathfrak {p}}+{\mathfrak {g}}^{1}\right)_{0},\cdots \end{array}}\right\}{\begin{array}{c}{\mbox{die entsprechenden (durch}}\\c\ {\mbox{dividierte) Energiebe-}}\\{\mbox{träge,}}\end{array}}\\&{\lambda _{\mu }}^{1},{\lambda _{\mu }}^{2},{\lambda _{\mu }}^{3},{\lambda _{\mu }}^{4},\ {\mbox{die Vorzeichen dieser Elektronenenergien für}}\\&{\mbox{den}}\ \mu {\mbox{ten Übergangsweg,}}\\&Z_{\mu }=V_{ik}^{1}V_{ke}^{1}V_{em}^{1}V_{mn}^{1}\ {\mbox{(bis auf einen Faktor) das Produkt der}}\\&{\mbox{Matrixelemente der Koppelung}}\ V^{1}\ {\mbox{im Zähler von (5,11) für}}\\&{\mbox{den}}\ \mu {\mbox{ten der 6 Übergangsfälle,}}\\&N_{\mu }=-{\frac {1}{8c^{3}}}\left(E_{i}-E_{k}\right)\left(E_{i}-E_{e}\right)\left(E_{i}-E_{m}\right)\ {\mbox{das Produkt der}}\\&{\mbox{Energiedifferenzen im Nenner des ersten Gliedes von (5,11)}}\\&{\mbox{für den}}\ \mu {\mbox{ten der 6 Übergangsfälle.}}\end{aligned}}\right.$

Im Matrixelement 4. Ordnung sind dann folgende Summationen auszuführen:

$\sum \limits _{\mu =1}^{6}$ über die 6 Übergangsfälle,

$\sum \limits _{\mathfrak {p}}={\frac {V}{h^{3}}}\int d{\mathfrak {p}}$ über alle Möglichkeiten der ersten Paarerzeugung,

$\sum \limits _{\sigma }$ über den Spin der Elektronen in Anfangs- und Zwischenzuständen;

$\sum \limits _{\mathrm {Perm} }$ über die 24 Reihenfolgen der Lichtquanten, d. h. die 24 Permutationen der 4 Indices $i$ in ${\mathfrak {g}}^{i}$, $g^{i}$ und ${\mathfrak {e}}^{i}$. (Bei Vertauschung der Emission des Lichtquants $-g^{3}$ mit der Absorption des Lichtquants $g^{1}$ wird der Impuls des Elektrons ${\mathfrak {p}}^{1}={\mathfrak {p}}+{\mathfrak {g}}^{1}$ mit ${\mathfrak {p}}^{1\prime }={\mathfrak {p}}+{\mathfrak {g}}^{3}$, und die Energie des Zwischenzustands ${\tfrac {E_{k}}{c}}=\mathrm {const} +g^{1}$ mit ${\tfrac {E_{k}^{\prime }}{c}}=\mathrm {const} +g^{3}$ vertauscht. Also ändern in den Formeln (5,11, 5,12) bei Vertauschung von Emission und Absorption Energie und Impuls der Lichtquanten ihr Vorzeichen, was bei unserer Bezeichnung (5,4) von se1ber durch Permutation der Indizes $i$ in ${\mathfrak {g}}^{i}$ bewirkt wird.)

Das Matrixelement kann daher geschrieben werden:

(5,13)

${\begin{array}{|c|}\hline \\H_{in}^{4}=C\int d{\mathfrak {p}}\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu =1}^{6}{\frac {Z_{\mu }}{N_{\mu }}}+V_{in}^{4}\\\hline \end{array}}$

Darin sind die Nenner:

${\begin{array}{|ccc|}\hline \\8N_{1}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{4}+{p_{0}}^{2}-g^{1}-g^{2}\right)&\left({p_{0}}^{4}+{p_{0}}^{3}+g^{4}\right)\\8N_{2}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{4}+{p_{0}}^{2}-g^{1}-g^{2}\right)&\left({p_{0}}^{2}+{p_{0}}^{3}+g^{3}\right)\\8N_{3}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{1}+{p_{0}}^{3}-g^{1}-g^{4}\right)&\left({p_{0}}^{2}+{p_{0}}^{3}+g^{3}\right)\\8N_{4}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{1}+{p_{0}}^{3}-g^{1}-g^{4}\right)&\left({p_{0}}^{1}+{p_{0}}^{2}+g^{2}\right)\\8N_{5}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{4}+{p_{0}}^{1}+{p_{0}}^{2}+{p_{0}}^{3}-g^{1}-g^{3}\right)&\left({p_{0}}^{1}+{p_{0}}^{2}+g^{2}\right)\\8N_{6}=\left({p_{0}}^{4}+{p_{0}}^{1}-g^{1}\right)&\left({p_{0}}^{4}+{p_{0}}^{1}+{p_{0}}^{2}+{p_{0}}^{3}-g^{1}-g^{3}\right)&\left({p_{0}}^{4}+{p_{0}}^{3}+g^{4}\right)\\\hline \end{array}}$

In den Zählern $Z_{\mu }$ ist über den Spin der Zwischenzustände (1, 2, 3) und des Anfangs- (=End-) Zustandes (4) zu summieren.

Die Spinsummation im Zustand eines Elektrons mit Impuls ${\mathfrak {p}}'$ und Energievorzeichen $\lambda '$ kann mit Hilfe des Operators

${\frac {1}{2}}\left(1-\lambda '{\frac {(\alpha {\mathfrak {p}}')+\beta mc}{{p_{0}}^{\prime }}}\right)$

ausgeführt werden, welcher 1 ergibt, angewandt auf den Zustand mit Impuls ${\mathfrak {p}}'$ und Energie ${\lambda _{0}}^{\prime }$, und 0 ergibt, angewandt auf den Zustand mit Impuls ${\mathfrak {p}}'$ und Energie $-\lambda 'p_{0}$.

Die Energievorzeichen $\lambda '$ ,$\lambda ^{2}$ ,$\lambda ^{3}$ ,$\lambda ^{4}$ der Zwischenzustände der Elektronen und die Produkte ${\mathfrak {p}}'$ der Jordan-Wignerschen Vorzeichenfunktion sind für die 6 Übergangsmöglichkeiten:

${\begin{array}{c|c|c|c|c|c}\hline \hline {\mbox{Vorzeichen}}&\lambda _{\mu }^{1}&\lambda _{\mu }^{2}&\lambda _{\mu }^{3}&\lambda _{\mu }^{4}&J'_{\mu }\\{\begin{array}{c|}\hline {\mbox{Fälle}}\end{array}}&&&&\\\hline \hline &&&&\\\mu =1&+&+&+&-&+\\\left\{{\begin{array}{c}\mu =2\\\mu =3\end{array}}\right.&{\begin{array}{c}+\\+\end{array}}&{\begin{array}{c}+\\+\end{array}}&{\begin{array}{c}-\\-\end{array}}&{\begin{array}{c}-\\-\end{array}}&{\begin{array}{c}-\\-\end{array}}\\\mu =4&+&-&-&-&+\\\left\{{\begin{array}{c}\mu =5\\\mu =6\end{array}}\right.&{\begin{array}{c}+\\+\end{array}}&{\begin{array}{c}-\\-\end{array}}&{\begin{array}{c}+\\+\end{array}}&{\begin{array}{c}-\\-\end{array}}&{\begin{array}{c}-\\-\end{array}}\end{array}}$

woraus man sieht, daß $J_{\mu }^{\prime }=\lambda _{\mu }^{2}\lambda _{\mu }^{3}$ ist.

Also werden die Zähler $Z_{\mu }$:

(5,15)

${\begin{array}{|lll|}\hline &&\\&{\begin{aligned}Z_{\mu }={\frac {\textrm {Spur}}{4}}\lambda _{\mu }^{2}\lambda _{\mu }^{3}&\left(\alpha {\mathfrak {e}}^{1}\right)\left(1-{\frac {\left(\alpha {\mathfrak {p}}^{1}\right)+\beta mc}{{p_{0}}^{1}}}\right)\\&\left(\alpha {\mathfrak {e}}^{2}\right)\left(1-\lambda _{\mu }^{2}{\frac {\left(\alpha {\mathfrak {p}}^{2}\right)+\beta mc}{{p_{0}}^{2}}}\right)\\&\left(\alpha {\mathfrak {e}}^{3}\right)\left(1-\lambda _{\mu }^{3}{\frac {\left(\alpha {\mathfrak {p}}^{3}\right)+\beta mc}{{p_{0}}^{3}}}\right)\\&\left(\alpha {\mathfrak {e}}^{4}\right)\left(1+{\frac {\left(\alpha {\mathfrak {p}}^{4}\right)+\beta mc}{{p_{0}}^{4}}}\right)\end{aligned}}&\\&{\textrm {mit}}&\\&\qquad {\begin{array}{c|cccccc}\mu =&1&2&3&4&5&6\\\hline \lambda _{\mu }^{2}=&+&+&+&-&-&-\\\lambda _{\mu }^{3}=&+&-&-&-&+&+\end{array}}&\\&&\\\hline \end{array}}$

(es ist $Z_{2}=Z_{3}$ und $Z_{5}=Z_{6}$).

§ 6. Entwicklung nullter Ordnung dieser Matrix ${\boldsymbol {H_{in}^{4}}}$ nach Lichtfrequenzen und Vergleich mit dem Heisenbergschen Subtraktionsglied

In (5,13; 5,9; 5,10; 5,14; 5,15) des vorigen Paragraphen wurde das Matrixelement $H_{in}^{4}$ der Diracschen Theorie für Streuung von Licht an Licht aufgestellt. Es ist eine Funktion der vier Lichtquanten, die an der Streuung teilnehmen, und soll, da das Licht als weich vorausgesetzt wird (0,1) nach den Impulsen ${\frac {{\mathfrak {g}}^{1}}{mc}}{\frac {{\mathfrak {g}}^{2}}{mc}}{\frac {-{\mathfrak {g}}^{3}}{mc}}{\frac {-{\mathfrak {g}}^{4}}{mc}}$ und Energien ${\frac {g^{1}}{mc}}{\frac {g^{2}}{mc}}{\frac {-g^{3}}{mc}}{\frac {-g^{4}}{mc}}$ der Lichtquanten entwickelt werden.

Neben der Entwicklung nach der Elektronenentladung $e$, für deren 4. Glied wir uns schon durch die Art der Störungsrechnung entschieden haben, führen wir also nun eine Entwicklung nach Lichtfrequenzen durch: Das Glied nullter Ordnung in der Entwicklung des Matrixelements $H_{in}^{4}$ nach Lichtfrequenzen $g^{i}/mc$ verschwindet, weil der Anteil, der vom Glied der gewöhnlichen Kopplung $V^{1}$ gebildet wird, vom Heisenbergschen Subtraktionsglied $V_{in}^{4}$ aufgehoben wird, wie wir im folgenden zeigen:

In nullter Ordnung sind die Nenner (5,14):

(6,1)

$N_{1}=N_{2}=N_{3}=N_{4}={p_{0}}^{3},\quad N_{5}=N_{6}=2{p_{0}}^{3}$

Die hierdurch dividierten Zähler (5,15):

(6,2)

$\left\{{\begin{aligned}&\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}=\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu }{\frac {1}{N_{\mu }}}{\frac {\textrm {Spur}}{4}}{\lambda _{\mu }}^{2}{\lambda _{\mu }}^{3}\\\cdot &\left(\alpha {\mathfrak {e}}^{1}\right)\left(1-{\frac {\left(\alpha {\mathfrak {p}}\right)+\beta mc}{p_{0}}}\right)\left(\alpha {\mathfrak {e}}^{2}\right)\left(1-\lambda ^{2}{\frac {\left(\alpha {\mathfrak {p}}\right)+\beta mc}{p_{0}}}\right)\\\cdot &\left(\alpha {\mathfrak {e}}^{3}\right)\left(1-\lambda ^{3}{\frac {\left(\alpha {\mathfrak {p}}\right)+\beta mc}{p_{0}}}\right)\left(\alpha {\mathfrak {e}}^{4}\right)\left(1+{\frac {\left(\alpha {\mathfrak {p}}\right)+\beta mc}{p_{0}}}\right)\end{aligned}}\right.$

werden nach Spurbildung und Summation über die 6 Fälle $\mu$:

(6,3)

$=\sum \limits _{\mathrm {Perm} }{\frac {-8}{{p_{0}}^{3}}}\left[\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)-6{\frac {\left({\mathfrak {pe}}^{1}\right)\left({\mathfrak {pe}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)}{{p_{0}}^{2}}}+5{\frac {\left({\mathfrak {pe}}^{1}\right)\left({\mathfrak {pe}}^{2}\right)\left({\mathfrak {pe}}^{3}\right)\left({\mathfrak {pe}}^{4}\right)}{{p_{0}}^{4}}}\right]$

Um den Vergleich dieses gewöhnlichen Gliedes mit dem Subtraktionsglied (5,9) durchzuführen, formt man es nach Heisenberg um in eine totale Ableitung

(6,4)

$\left\{{\begin{aligned}={\frac {8}{3}}\sum \limits _{\mathrm {Perm} }&\left({\mathfrak {e}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)\left({\mathfrak {e}}^{2}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)\left({\mathfrak {e}}^{3}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)\left({\mathfrak {e}}^{4}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)p_{0},\\&\left(\left({\mathfrak {e}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)={{\mathfrak {e}}_{x}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}_{x}}}+{{\mathfrak {e}}_{y}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}_{y}}}+{{\mathfrak {e}}_{z}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}_{z}}}\right)\end{aligned}}\right.$

und geht vom Matrixelement (6,4) zur entsprechenden (in $\xi \pm {\mathfrak {r}}$) gemischten Energiedichte über:

${\begin{aligned}&C\int d{\mathfrak {p}}\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}\rightarrow C\int e^{{\frac {i}{\hbar }}({\mathfrak {pr}})}\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}d{\mathfrak {p}}\\=&{\frac {8}{3}}C\sum \limits _{\mathrm {Perm} }\int e^{{\frac {i}{\hbar }}({\mathfrak {pr}})}\left({\mathfrak {e}}^{1}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)\left({\mathfrak {e}}^{2}{\frac {\partial }{\partial {\mathfrak {p}}}}\right)\left({\mathfrak {e}}^{3}{\frac {\partial }{\partial {\mathfrak {p}}}}\right){\mathfrak {e}}^{4}\left({\frac {\partial }{\partial {\mathfrak {p}}}}\right)p_{0}d{\mathfrak {p}}\\=&-{\frac {64\pi }{3}}C\sum \limits _{\mathrm {Perm} }{\frac {\left({\mathfrak {e}}^{1}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{2}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{3}{\mathfrak {r}}\right)\left({\mathfrak {e}}^{4}{\mathfrak {r}}\right)}{|{\mathfrak {r}}|^{4}}}=-\left(g^{1}g^{2}\left|V^{4}\right|-g^{3}-g^{4}\right).\end{aligned}}$

$\left[\int p_{0}e^{{\frac {i}{\hbar }}({\mathfrak {pr}})}d{\mathfrak {p}}=-{\frac {8\pi \hbar ^{4}}{|{\mathfrak {r}}|^{4}}}\right.$ wenn man das Integral künstlich konvergent macht, und für $|{\mathfrak {r}}|\ll {\frac {\hbar }{mc}}$berechnet.${\Bigg ]}$ Damit ist die Behauptung bewiesen: In nullter Ordnung der Entwicklung nach Lichtfrequenzen gibt es infolge des Subtraktionsgliedes $V^{4}$ keine Streuung von Licht an Licht.

Würde das Heisenbergsche Glied (5,9) nicht zum gewöhnlichen Matrixelement addiert, so ergäbe die Diracsche Theorie eine für genügend lange Wellen beliebig große Streuung von Licht an Licht im Widerspruch zur Erfahrung (5,9; 5,10).

§ 7. Nachweis der Identität der aus der Diracschen Theorie folgenden Matrix ${\boldsymbol {H_{in}^{4}}}$ mit der oben aufgestellten Wechselwirkungsenergie ${\boldsymbol {{\bar {U}}_{1}}}$ der Lichtquanten

Es kann nun leicht gezeigt werden, daß die eben aufgestellte Matrix $H_{in}^{4}$ der Diracschen Theorie (5,13), deren Übergangselemente die Streuung von Licht an Licht beschreiben, mit der früher angeschriebenen Wechselwirkung der Lichtquanten (2,21) identisch ist:

a) Das Matrixelement $H_{in}^{4}$ (5,13; 5,14; 5,15) der Diracschen Theorie kann als einfaches Integral $\int dV$ über ein Produkt der vier ebenen Lichtwellen (5,2): ${\underset {g^{1}}{\mathfrak {A}}},{\underset {g^{2}}{\mathfrak {A}}},{\underset {g^{3}}{\mathfrak {A}}},{\underset {g^{4}}{\mathfrak {A}}}={\mathfrak {e}}^{4}e^{{\frac {i}{k}}\left({\mathfrak {g}}^{4}\xi \right)}\cdot {\sqrt {\frac {ch\hbar }{\left|g^{4}\right|V}}}$ geschrieben werden:

Denn wegen des Impulssatzes ${\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}+{\mathfrak {g}}^{3}+{\mathfrak {g}}^{4}=0$ ist

(7,1)

$\left\{{\begin{aligned}&H_{in}^{4}={\frac {e^{4}}{16c^{3}h^{3}}}\sum \limits _{\mathrm {Perm} }\sum \limits _{\mu }\mathrm {Spur} \int d{\mathfrak {p}}\int dV\\\cdot &(\alpha {\underset {g^{1}}{\mathfrak {A}}})\left({\frac {1-{\frac {\left(\alpha ,{\mathfrak {p}}+{\mathfrak {g}}^{1}\right)+\beta mc}{\left({\mathfrak {p}}+{\mathfrak {g}}^{1}\right)_{0}}}}{p_{0}+\left({\mathfrak {p}}+{\mathfrak {g}}^{1}\right)_{0}-g^{1}}}\right)(\alpha {\underset {g^{2}}{\mathfrak {A}}})\left({\frac {1-{\frac {\left(\alpha ,{\mathfrak {p}}+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\right)+\beta mc}{\left({\mathfrak {p}}+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\right)_{0}}}}{p_{0}+\left({\mathfrak {p}}+{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\right)-g^{1}-g^{2}}}\right)\\\cdot &(\alpha {\underset {g^{3}}{\mathfrak {A}}})\left({\frac {1-{\frac {\left(\alpha ,{\mathfrak {p}}+{\mathfrak {g}}^{4}\right)+\beta mc}{\left({\mathfrak {p}}+{\mathfrak {g}}^{4}\right)_{0}}}}{p_{0}+\left({\mathfrak {p}}-t\right)_{0}+g^{4}}}\right)(\alpha {\underset {g^{4}}{\mathfrak {A}}})\left(1+{\frac {(\alpha {\mathfrak {p}})+\beta mc}{p_{0}}}\right)+V_{in}^{4}.\end{aligned}}\right.$

b) Dieses zusammengesetzte Matrixelement $H_{in}^{4}$ kann als einfaches Matrixelement einer Funktion ${\bar {U}}$ des Strahlungsfeldes aufgefaßt werden, welche das Integral über einen Ausdruck in den Potentialen und ihren (mit $\hbar /mc$ multiplizierten) Ableitungen ist. Dem Grad der Ableitungen entspricht die Ordnung der Entwicklung nach Lichtquantenenergien:

Denn denkt man sich im ersten Teil von (7,1) die Spurbildung, Integration über ${\mathfrak {p}}$, Summation über $\mu$ ausgeführt und nach Lichtquantenenergien $g^{i}/mc$ entwickelt, so entsteht ein Ausdruck der Form:

(7,2)

$\left\{{\begin{aligned}H_{in}^{4}&={\frac {e^{4}}{16c^{3}h^{3}}}\sum \limits _{\mathrm {Perm} }\int dV\left[{\underset {g^{1}}{\mathfrak {A}}}{\underset {g^{2}}{\mathfrak {A}}}{\underset {g^{3}}{\mathfrak {A}}}{\underset {g^{4}}{\mathfrak {A}}}+{\frac {{\mathfrak {g}}^{1}}{mc}}{\underset {g^{1}}{\mathfrak {A}}}{\underset {g^{2}}{\mathfrak {A}}}{\underset {g^{3}}{\mathfrak {A}}}{\underset {g^{4}}{\mathfrak {A}}}+\cdots +\right.\\&\left.+{\frac {{\mathfrak {g}}^{1}}{mc}}{\frac {g^{2}}{mc}}{\frac {{\mathfrak {g}}^{3}}{mc}}{\frac {{\mathfrak {g}}^{4}}{mc}}{\underset {g^{1}}{\mathfrak {A}}}{\underset {g^{2}}{\mathfrak {A}}}{\underset {g^{3}}{\mathfrak {A}}}{\underset {g^{4}}{\mathfrak {A}}}+\cdots \right]+V_{in}^{4}\\&={\frac {e^{4}}{16c^{3}h^{3}}}\sum \limits _{\mathrm {Perm} }\int dV\left[{\underset {g^{1}}{\mathfrak {A}}}{\underset {g^{2}}{\mathfrak {A}}}{\underset {g^{3}}{\mathfrak {A}}}{\underset {g^{4}}{\mathfrak {A}}}+\left({\frac {\hbar }{mc}}{\frac {\partial }{\partial x}}{\underset {g^{1}}{\mathfrak {A}}}\right){\underset {g^{2}}{\mathfrak {A}}}{\underset {g^{3}}{\mathfrak {A}}}{\underset {g^{4}}{\mathfrak {A}}}+\cdots \right.\\&\left.+\left({\frac {\hbar }{mc}}\right)^{4}\left({\frac {\partial }{\partial x}}{\underset {g^{1}}{\mathfrak {A}}}\right)\left({\frac {1}{c}}{\frac {\partial }{\partial t}}{\underset {g^{2}}{\mathfrak {A}}}\right)\left({\frac {\partial }{\partial x}}{\underset {g^{3}}{\mathfrak {A}}}\right)\left({\frac {1}{c}}{\frac {\partial }{\partial t}}{\underset {g^{4}}{\mathfrak {A}}}\right)+\cdots \right]+V_{in}^{4}\\&=\left(g^{1}g^{2}\left|\int U_{1}dV\right|-g^{3}-g^{4}\right)\ {\textrm {mit}}\\U_{1}&={\frac {e^{4}}{16c^{3}h^{3}}}\left[{\mathfrak {AAAA}}+{\frac {\hbar }{mc}}{\frac {\partial {\mathfrak {A}}}{\partial x}}{\mathfrak {AAA}}+\cdots \right.\\&\left.+\left({\frac {\hbar }{mc}}\right)^{4}\left({\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)\left({\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)+\cdots \right].\end{aligned}}\right.$

Darin ist das Heisenbergsche Glied

${\begin{aligned}V^{4}={\frac {-1}{12\pi ^{2}}}\cdot \left({\frac {e^{2}}{\hbar c}}\right)^{2}{\frac {1}{\hbar c}}\lim \limits _{{\mathfrak {r}}\rightarrow 0}\int {\frac {\left({\mathfrak {A}}(\xi )\cdot {\mathfrak {r}}\right)^{4}}{|{\mathfrak {r}}|^{4}}}dV\qquad \\\rightarrow -{\frac {1}{12\pi ^{2}}}{\frac {e^{4}}{\hbar ^{3}c^{3}}}\cdot {\frac {1}{5}}\int ({\mathfrak {AA}})({\mathfrak {AA}})dV\end{aligned}}$

mit enthalten, wenn man die Limesbildung ${\mathfrak {r}}\rightarrow 0$ durch Winkelmittelung über ${\mathfrak {r}}$ ausführt.

c) Die Glieder, Welche die Potentiale ${\mathfrak {A}}$ direkt enthalten und sich nicht durch Feldstärken $F_{ik}$ ausdrücken lassen, also (u. a.) die Entwicklungsglieder nullter, 1., 2., 3. Ordnung nach Lichtfrequenzen müssen verschwinden.

Denn da die Voraussetzungen, von denen diese Rechnungen ausgehen, eichinvariant sind, müssen es auch die Resultate sein, d. h. es können nur die Kombinationen aus den Ableitungen der Potentiale vorkommen, welche Feldstärken oder Ableitungen von Feldstärken bedeuten.

Das Verschwinden des nullten Entwicklungsgliedes von $H_{in}^{4}$ nach $g^{i}/mc$, welches durch Kompensation mit dem Heisenbergschen Glied $V_{in}^{4}$ zustande kam, ist damit aus den Forderungen der Eichinvarianz verständlich, welche ja auch der Grund für das Glied $V^{4}$ war. Das Verschwinden der 1., 2. und 3. Ordnung in der Entwicklung nach $g^{i}/mc$ soll später (§ 9) für die 1. Ordnung allgemein, für die 2. und 3. Ordnung an einigen Spezialfällen durch direktes Ausrechnen bestätigt werden.

Also bleibt von unserem Ausdruck (7,2) nur

${\begin{aligned}U_{1}&={\frac {e^{4}}{16c^{3}h^{3}}}\left({\frac {\hbar }{mc}}\right)^{4}\left[\left({\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)\left({\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)\right.\\&\left.+\left({\frac {\hbar }{mc}}{\frac {\partial }{\partial x}}{\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {\hbar }{mc}}{\frac {\partial }{\partial x}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)\left({\frac {\partial {\mathfrak {A}}}{\partial x}}\right)\left({\frac {1}{c}}{\frac {\partial {\mathfrak {A}}}{\partial t}}\right)+\cdots \right].\end{aligned}}$

oder

(7,3)

$U_{1}={\frac {\hbar c}{c^{2}}}{\frac {1}{{E_{0}}^{2}}}{\frac {1}{16\cdot (2\pi )^{3}}}\left[FFFF+{\frac {\hbar }{mc}}{\frac {\partial F}{\partial x}}{\frac {\hbar }{mc}}{\frac {\partial F}{\partial x}}FF+\dots \right]$

übrig und es ist

(7,4)

$H_{in}^{4}=\left(g^{1}g^{2}\left|\int U_{1}dV\right|-g^{3}-g^{4}\right)$

d. h. die Wechselwirkung der Lichtquanten kann in der Tat durch ein anschauliches Gesetz beschrieben werden und dies ist für weiches Licht von der oben erwarteten Form (1,4), also aus Invarianzgründen von der Form (2,21).

Wir verzichten dabei auf Glieder höherer als 4. Ordnung in der Entwicklung nach Lichtquantenenergien, also auf die Glieder mit den Ableitungen der Feldstärken, ferner, wie schon durch die Art der Störungsrechnung vorgeschrieben ist, auf Glieder höherer als 4. Ordnung in der Entwicklung der Feldgleichungen nach der Elektronenladung, d. h. auf höhere als 4. Potenzen in den Feldstärken, d. h. wir beschränken uns auf nicht zu starke und nicht zu schnell veränderliche Felder, in denen keine Paare erzeugt werden können und von denen außerdem vorausgesetzt ist, daß sie keine Elektronen enthalten, die an der Strahlung teilnehmen.

(7,5)

$\left\{{\begin{aligned}&({\mbox{Feldstärke klein gegen die Feldstärke am Rand des Elektrons:}}\\&\qquad \left|F_{ik}\right|\ll E_{0},\\&{\mbox{Wellenlängen groß gegen die Comptonwellenlänge d. h. als}}\\&{\mbox{invariante Bedingung (0,1; 5,2):}}\\&\left.\left({\frac {\partial F_{ik}}{\partial x}}\right)^{2}+\left({\frac {\partial F_{ik}}{\partial y}}\right)^{2}+\left({\frac {\partial F_{ik}}{\partial z}}\right)^{2}-{\frac {1}{c^{2}}}\left({\frac {\partial F_{ik}}{\partial t}}\right)^{2}\ll 2\left({\frac {mc}{\hbar }}\right)^{2}\left(F_{ik}\right)^{2}.\right)\end{aligned}}\right.$

III. Teil

§ 8. Ausrechnung des Matrixelementes für Streuung von Licht an Licht (im Glied 4. Ordnung der Entwicklung nach Lichtfrequenzen) für zwei Spezialfälle zur Bestimmung der Zahlenkoeffizienten $\alpha$, $\beta$ in der Wechselwirkung von Licht mit Licht

$\left(\alpha =-{\frac {1}{360\pi ^{2}}},\ \beta =-{\frac {7}{360\pi ^{2}}}\right)$

Bisher wurde die Wechselwirkung der Lichtquanten bis auf zwei Konstanten $\alpha$, $\beta$ bestimmt (2,21). Um diese beiden Konstanten auszurechnen, betrachten wir jetzt einen speziellen Prozeß, in welchen zwei Lichtquanten gleicher Energie und entgegengesetzter Impulse aufeinander stoßen und ihre Impulse austauschen (oder, was hiervon nicht unterschieden werden kann, ungestreut durcheinander hindurchgehen).

Die Polarisationen der beiden primären Quanten sollen einander gleich sein, ebenso die der sekundären. Um zwei Konstanten zu berechnen, brauchen wir zwei Spezialisierungen: In der ersten a) möge die Polarisation der primären Lichtquanten senkrecht auf der Polarisation der sekundären stehen, im zweiten Fall b) mögen alle vier Lichtquanten dieselbe Polarisation haben.

Mit der Bezeichnung:

${\mathfrak {g}}^{1}={\mathfrak {g}},\qquad g^{1}=g$

soll also sein:

(8,1)

${\begin{array}{ccccc}&{\textrm {I}}&&{\textrm {I}}\\{\textrm {II}}&{\begin{array}{c|c}{\mathfrak {g}}^{1}=+{\mathfrak {g}}&{\mathfrak {g}}^{2}=-{\mathfrak {g}}\\\hline {\mathfrak {g}}^{3}=+{\mathfrak {g}}&{\mathfrak {g}}^{4}=-{\mathfrak {g}}\end{array}}&&{\begin{array}{c|c}g^{1}=+g&g^{2}=+g\\\hline g^{3}=-g&g^{4}=-g\end{array}}&{\textrm {II}}\end{array}}$

und in einem Koordinatensystem, in dessen $x$-Achse der Vektor ${\mathfrak {g}}$ liegt, soll gelten:

(8,2)

${\begin{array}{c|c}{\text{im Spezialfall a):}}&{\text{im Spezialfall b):}}\\\hline \left\{{\begin{array}{c}\Vert \ {\text{Impulse und}}\ \bot \ {\text{Polarisationen}}\\{\begin{array}{rcc}(x)&(y)&(z)\\{\mathfrak {g}}=(g,&0,&0)\\{\mathfrak {e}}^{1}={\mathfrak {e}}^{2}=(0,&1,&0)\\{\mathfrak {e}}^{3}={\mathfrak {e}}^{4}=(0,&0,&1)\end{array}}\end{array}}\right.&{\begin{array}{c}\Vert \ {\text{Impulse und}}\ \bot \ {\text{Polarisationen}}\\{\begin{array}{rcc}(x)&(y)&(z)\\{\mathfrak {g}}=(g,&0,&0)\\{\mathfrak {e}}^{1}={\mathfrak {e}}^{2}=(0,&1,&0)\\{\mathfrak {e}}^{3}={\mathfrak {e}}^{4}=(0,&1,&0)\end{array}}\end{array}}\end{array}}$

Fig. 2

Wir rechnen nun für diese zwei Spezialfälle [(8,2 a), (8,2 b)] das Diracsche Matrixelement $H_{in}^{4}$ [(5,13), (5,14), (5,15)] (im Glied 4. Ordnung der Entwicklung nach Lichtfrequenzen $g^{1}/mc$) und das Matrixelement der Feldfunktion ${\bar {U}}_{1}$ (2,21) aus, setzen beide einander gleich:

(8,3)

$H_{in}^{4}={\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left(g^{1}g^{2}\left|\int \left[\alpha \left({\mathfrak {D}}^{2}-{\mathfrak {B}}^{2}\right)^{2}+\beta ({\mathfrak {DB}})^{2}\right]dV\right|-g^{3}-g^{4}\right)$

und erhalten dadurch zwei lineare Bestimmungsgleichungen für die Konstanten $\alpha$ und $\beta$.

(Dabei ist allerdings die Definition des Spezialfalles, in welchem der Endzustand $-g^{3}$, $-g^{4}$ gleich dem Anfangszustand $g^{1}$, $g^{2}$ ist, in dem also gar keine Wirkliche Streuung stattfindet, nicht wörtlich zu nehmen. Sie muß vielmehr so aufgefaßt werden, daß die Endlichtquanten $-g^{3}$, $-g^{4}$ nur relativ Wenig von den Anfangslichtquanten $g^{1}$, $g^{2}$ abweichen, daß nach dieser Abweichung entwickelt wird und daß die Glieder nullter Ordnung dieser Entwicklung verglichen werden.)

Zunächst berechnen wir die Matrixelemente der Feldfunktionen ${\bar {U}}_{1}$ (2,21) für die beiden Spezialfälle (8,2a), (8,2b):

$\left({\begin{array}{cl}[..]&{\text{Vektorprodukt}}\\(..)&{\text{Skalares Produkt}}\\|...|&{\text{Determinante}}\end{array}}\right)$.

${\begin{array}{ll|l|l}(8,4)&\left\{{\begin{array}{c}{\text{Nach}}\left.{\begin{array}{cc}(5,2),&(5,3)\\(2,2),&(2,6)\end{array}}\right\}{\text{ist das Matrixelement}}\\{\text{der Feldfunktionen}}:\end{array}}\right.&{\frac {1}{D}}\left(g^{1}g^{2}\left|\int ({\mathfrak {BD}})^{2}dV\right|-g^{3}-g^{4}\right)&{\frac {1}{D}}\left(g^{1}g^{2}\left|\int ({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2})^{2}dV\right|-g^{3}-g^{4}\right)\\\hline (8,5)&\left\{{\begin{array}{c}{\text{gleich:}}\\{\text{Darin bedeutet}}\ D\ {\text{die Konstante}}\\D=\left({\frac {ch\hbar }{V}}\right)^{2}{\frac {1}{\hbar ^{4}}}{\frac {V}{\sqrt {g^{1}g^{2}g^{3}g^{4}}}}\end{array}}\right.&{\begin{array}{c}\sum \limits _{\textrm {Perm}}\left|{\mathfrak {e}}^{1}{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right|\left|{\mathfrak {e}}^{3}{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right|g^{1}g^{3}\\\\\\\end{array}}&{\begin{array}{c}\sum \limits _{\textrm {Perm}}\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)g^{1}g^{2}g^{3}g^{4}\\-2\sum \limits _{\textrm {Perm}}\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)g^{1}g^{2}\left(\left[{\mathfrak {e}}^{3}{\mathfrak {g}}^{3}\right]\left[{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right]\right)\\+\sum \limits _{\textrm {Perm}}\left(\left[{\mathfrak {e}}^{1}{\mathfrak {g}}^{1}\right]\left[{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right]\right)\left(\left[{\mathfrak {e}}^{3}{\mathfrak {g}}^{3}\right]\left[{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right]\right)\end{array}}\\\hline (8,5)&\left\{{\begin{array}{c}{\text{Dies wird im Fall der}}\ \bot \ Polarisationen:\\{\begin{array}{rcc}(x)&(y)&(z)\\{\mathfrak {e}}^{1}={\mathfrak {e}}^{2}=(0,&1,&0)\\{\mathfrak {e}}^{3}={\mathfrak {e}}^{4}=(0,&0,&1)\end{array}}\end{array}}\right.&{\begin{array}{cc}=2&\left[{\begin{array}{cc}2{{\mathfrak {g}}_{x}}^{1}{{\mathfrak {g}}_{x}}^{2}g^{3}g^{4}&+2{{\mathfrak {g}}_{x}}^{3}{{\mathfrak {g}}_{x}}^{4}g^{1}g^{2}\\-{{\mathfrak {g}}_{x}}^{1}{{\mathfrak {g}}_{x}}^{3}g^{2}g^{4}&-{{\mathfrak {g}}_{x}}^{1}{{\mathfrak {g}}_{x}}^{4}g^{2}g^{3}\\-{{\mathfrak {g}}_{x}}^{2}{{\mathfrak {g}}_{x}}^{3}g^{1}g^{4}&-{{\mathfrak {g}}_{x}}^{2}{{\mathfrak {g}}_{x}}^{4}g^{1}g^{3}\end{array}}\right]\end{array}}&{\begin{array}{c}{\begin{array}{c}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)\\\\\\\end{array}}\left[{\begin{array}{c}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)\\-2\left({\mathfrak {g}}_{x}^{1}{\mathfrak {g}}_{x}^{3}\right)g^{3}g^{4}\\+g^{1}g^{2}g^{3}g^{4}\end{array}}\right]\end{array}}\\\hline (8,6)&\left\{{\begin{array}{c}{\text{und bei weiterer Spezialisierung}}\\{\text{auf}}\ \Vert \ {\text{und entgegengesetzte Impulse,}}\\{\text{also im}}\ Spezialfall\ {\text{(8,2a):}}\end{array}}\right.&{\begin{array}{c}\\\\=-8|{\mathfrak {g}}|4\end{array}}&{\begin{array}{c}\\\\+32|{\mathfrak {g}}|4\end{array}}\\\hline (8,6')&\left\{{\begin{array}{c}{\text{Dagegen im Fall der}}\ \Vert \ Polarisationen:\\{\begin{array}{rcc}(x)&(y)&(z)\\{\mathfrak {e}}^{1}={\mathfrak {e}}^{2}={\mathfrak {e}}^{3}={\mathfrak {e}}^{4}=(0,&1,&0)\end{array}}\end{array}}\right.&{\begin{array}{cc}\\\\=0\end{array}}&{\begin{array}{c}\\\\=\sum \limits _{\textrm {Perm}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)-2\left(g^{1}g^{2}\right)g^{3}g^{4}+g^{1}g^{2}g^{3}g^{4}\right]\end{array}}\\\hline (8,7)&\left\{{\begin{array}{c}{\text{und bei weiterer Spezialisierung}}\\{\text{auf}}\ \Vert \ {\text{und entgegengesetzte Impulse,}}\\{\text{also im}}\ Spezialfall\ {\text{(8,2b):}}\end{array}}\right.&{\begin{array}{c}\\\\=0\end{array}}&{\begin{array}{c}\\\\=64|g|4\end{array}}\end{array}}$

Damit sind (8.6)^{[WS 1]}, (8,7) die Matrixelemente der beiden Feldfunktionen (2,21) in den beiden Spezialfällen (8,2a) und (8,2b) ausgerechnet. Wie man sieht, sind die Übergänge a) paralleler Polarisation durch das Wechselwirkungsglied $\left({\mathfrak {D}}^{2}-{\mathfrak {B}}^{2}\right)^{2}$ allein bestimmt. Das andere Glied $({\mathfrak {DB}})^{2}$ gibt hier keinen Beitrag, weil bei einer ebenen Welle ${\mathfrak {D}}\bot {\mathfrak {B}}$ ist. Zu den Übergängen b) senkrechter Polarisation aber tragen beide Wechselwirkungsglieder $({\mathfrak {DB}})^{2}$ und ($\left({\mathfrak {D}}^{2}-{\mathfrak {B}}^{2}\right)^{2}$ bei, weil darin sowohl senkrechte wie parallele Polarisationen kombiniert werden können.

Wir müssen nun das Matrixelement $H_{in}^{4}$ [(5,13), (5,14), (5,15)] der Diracschen Theorie für dieselben zwei Übergänge (8,2a, b) ausrechnen, und behandeln zunächst die Summation $\sum \limits _{\textrm {Perm}}$ über die 24 Reihenfolgen der Lichtquanten, die darin vorkommen.

Zwischen den Lichtquanten ist durch die Spezialisierung (8,2a, b) eine Symmetrie hergestellt, die es erlaubt, die Summe über einige ihrer Permutationen leicht auszuführen:

Wie (8,1), (8,2) zeigt, hängt das Matrixelement nur noch vom Vektor ${\mathfrak {g}}$ und von der Zahl $g$ ab und die Vertauschung

$\mathrm {I} \quad$	von ${\mathfrak {g}}^{1}$ mit ${\mathfrak {g}}^{2}$ und von $g^{3}$ mit $g^{4}$ bedeutet im Matrixelement    einen Wechsel des Vorzeichens von ${\mathfrak {g}}$	${\mathfrak {g}}\rightarrow -{\mathfrak {g}}$,
	aber Bestehenbleiben des Vorzeichens von $g$	$g\rightarrow +g$,
	und Bestehenbleiben der Polarisationen	$p_{y}\rightarrow p_{y},\ p_{z}\rightarrow p_{z}$.

Die Vertauschung

$\mathrm {II} \quad$	von ${\mathfrak {g}}^{1}$ mit ${\mathfrak {g}}^{2}$ und von $g^{2}$ mit $g^{4}$ dagegen
	Bestehenbleiben des Vorzeichens von ${\mathfrak {g}}$	${\mathfrak {g}}\rightarrow +{\mathfrak {g}}$,
	Wechsel des Vorzeichens von $g$	$g\rightarrow -g$,
	und Vertauschung der Polarisationen	$p_{y}\rightarrow p_{z},\ p_{z}\rightarrow p_{y}$.

Die Vierergruppe von Vertauschungen, die von diesen Permutationen I, II erzeugt wird (I, II, Produkt I·II, Identität), kann also in den Formeln schematisch ausgeführt werden. Die sechs Rest-„Klassen“ aller 24 Permutationen nach diesen vier aber müssen einzeln ausgerechnet werden. Sie können repräsentiert werden durch die folgenden sechs Reihenfolgen der Lichtquanten, zu denen bestimmte Reihenfolgen der Polarisationen und bestimmte Zwischenzustände der Elektronen gehören.

(8,8)

$\left\lbrace {\begin{array}{c|c|c|c}{\begin{array}{c}{\overset {8,8\alpha }{\overbrace {\textrm {Reihenfolge}} }}\\{\text{der}}\\Lichtquanten\end{array}}&{\begin{array}{c}{\overset {8,8\beta }{\overbrace {Polarisationen} }}\\{\text{im Fall a)}}\\{\text{in (5,15)}}\end{array}}&{\begin{array}{c}{\overset {8,8\gamma }{\overbrace {Polarisationen} }}\\{\text{im Fall b)}}\\{\text{einzusetzen}}\end{array}}&{\begin{array}{c}{\underset {\overbrace {\qquad \qquad \qquad \qquad \qquad \quad } }{8,8\delta }}{\underset {\overbrace {\qquad \qquad \qquad \qquad } }{8,8\epsilon }}\\{\begin{array}{c}Zwischenzust{\ddot {a}}nde\\{\text{in (5,14), (5,15) einzusetzen}}\\{\color {white}g}\end{array}}\end{array}}\\\hline &&\\{\begin{array}{c}{\color {white}g^{\color {white}1}}\\\hline \hline g^{1}g^{2}g^{3}g^{4}\\g^{1}g^{2}g^{4}g^{3}\\g^{1}g^{3}g^{4}g^{2}\\g^{1}g^{4}g^{3}g^{2}\\g^{1}g^{4}g^{2}g^{3}\\g^{1}g^{3}g^{2}g^{4}\end{array}}&{\begin{array}{ccccc}{\mathfrak {e}}^{1}&{\mathfrak {e}}^{2}&{\mathfrak {e}}^{3}&{\mathfrak {e}}^{4}\\\hline \hline y&y&z&z^{\color {white}1}\\y&y&z&z^{\color {white}1}\\y&z&z&y^{\color {white}1}\\y&z&z&y^{\color {white}1}\\y&z&y&z^{\color {white}1}\\y&z&y&z^{\color {white}1}\end{array}}&{\begin{array}{cccc}{\mathfrak {e}}^{1}&{\mathfrak {e}}^{2}&{\mathfrak {e}}^{3}&{\mathfrak {e}}^{4}\\\hline \hline y&y&y&y^{\color {white}{1}}\\y&y&y&y^{\color {white}{1}}\\y&y&y&y^{\color {white}{1}}\\y&y&y&y^{\color {white}{1}}\\y&y&y&y^{\color {white}{1}}\\y&y&y&y^{\color {white}{1}}\end{array}}&{\begin{array}{c|c|c|c|c|c|c|cc}{\mathfrak {p}}^{1}&{\mathfrak {p}}^{2}&{\mathfrak {p}}^{3}&{\mathfrak {p}}^{4}&g^{1}&g^{2}&g^{3}&g^{4}\\\hline \hline {\mathfrak {p+g}}&{\mathfrak {p}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&g&-g&-g\\{\mathfrak {p+g}}&{\mathfrak {p}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&g&-g&-g\\{\mathfrak {p+g}}&{\mathfrak {p}}+2{\mathfrak {g}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&-g&-g&+g\\{\mathfrak {p+g}}&{\mathfrak {p}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&-g&-g&+g\\{\mathfrak {p+g}}&{\mathfrak {p}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&-g&g&-g\\{\mathfrak {p+g}}&{\mathfrak {p}}+2{\mathfrak {g}}&{\mathfrak {p+g}}&{\mathfrak {p}}&g^{\color {white}1}&-g&g&-g\end{array}}\end{array}}\right.$[WS 2]

Das Matrixelement (5,13) ist eine Summe von Produkten aus Zählern $Z_{\mu }$, welche die zusammengesetzten Matrixelemente (5,15), und reziproken Nennern $1/N_{\mu }$, welche Energiedifferenzen bedeuten (5,14).

Schon in den Zählern kann über die Permutation der Polarisationen (II: $p_{y}\rightarrow p_{z},\ p_{z}\rightarrow p_{y}$) summiert werden, weil die Polarisationsrichtungen $p_{y}$ und $p_{z}$ nur im Zähler und nicht in den Nennern Vorkommen und weil die nachfolgende Mittelung über die Winkel von ${\mathfrak {p}}$ diese beiden Polarisationsrichtungen nicht unterscheidet $\left({\overline {{p_{y}}^{2}{p_{x}}^{n}}}={\overline {{p_{z}}^{2}{p_{x}}^{n}}}\right)$. Man kann also schon im Zähler $p_{y}^{2}=p_{z}^{2}$ setzen (in Ausdrücken 2. Ordnung von $y$).

Über die Permutation der Lichtquantenenergien kann schon im reziproken Nenner $1/N_{\mu }$ (5,14) summiert werden, weil sie im Zähler (5,15) nicht vorkommen, d. h. man kann nach Ausrechnung der reziproken Nenner alle ungeraden Potenzen von $g$ streichen.

Die Permutation der Impulse aber (I: ${\mathfrak {g}}\rightarrow -{\mathfrak {g,}}$) kann erst nach Multiplikation der Zähler mit den reziproken Nennern durchgeführt werden, weil ${\mathfrak {g}}$ in beiden vorkommt, d. h. bei dieser Multiplikation sind alle ungeraden Potenzen von ${\mathfrak {g}}_{x}\dots$ fortzulassen.

Nach diesen Vereinfachungen besteht dann die Summation $\sum \limits _{\textrm {Perm}}$ über die 24 Lichtquantenpermutationen nur noch: in der Summation des Matrixelements über die sechs Reihenfolgen (8,8) und der Multiplikation des Resultate mit dem Faktor 4.

Die reziproken Nenner $1/N_{\mu }$ werden, wie man durch Einsetzen der Spezialisierung (8,8, $\epsilon$) in (5,14), Entwicklung nach Lichtfrequenzen$g/mc$, ${\mathfrak {g}}m/c$ bis zur 4. Ordnung und Streichen der ungeraden Potenzen von $g$ findet:

(Die Zahl der $i$ten Zeile und der $k$ten Spalte der Tabelle bedeutet den Beitrag des Entwicklungsgliedes, das ganz oben in der $k$ten Spalte steht, für den Ausdruck, der ganz links in der $i$ten Zeile steht.)

Vgl. Gl. (8,9).

Für die Zähler des Matrixelements im Fall a) erhält man, indem man zur Spezialisierung auf $\bot$ Polarisationen (8,8, $\beta$) in (5,15) einsetzt, die Spur bildet und in den in $p$ quadratischen Gliedern ${p_{z}}^{2}$ durch ${p_{y}}^{3}$ ersetzt:

Für die Reihenfolge: $g^{1}g^{2}g^{3}g^{4}$ und $g^{1}g^{2}g^{4}g^{3}$

${\begin{aligned}Z_{\mu }&=S_{1}+2{p_{y}}^{2}\left[{\frac {{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{2}}}-{\frac {{\lambda _{\mu }}^{2}}{{p_{0}}^{3}{p_{0}}^{4}}}-{\frac {{\lambda _{\mu }}^{2}+{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{4}}}+{\frac {1}{{p_{0}}^{2}{p_{0}}^{3}}}-{\frac {2{\lambda _{\mu }}^{2}}{{p_{0}}^{1}{p_{0}}^{3}}}\right]\\&-{\frac {1}{{p_{0}}^{1}{p_{0}}^{2}{p_{0}}^{3}{p_{0}}^{4}}}\left[S_{2}+8{p_{y}}^{2}{p_{z}}^{2}+2{p_{y}}^{2}\left[-\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)-\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)-\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)-\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)+2\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{4}\right)-2\left(mc\right)^{2}\right]\right]\end{aligned}}$

Für die Reihenfolge: $g^{1}g^{2}g^{3}g^{4}$ und $g^{1}g^{4}g^{3}g^{2}$

${\begin{aligned}Z_{\mu }&=S_{1}+2{p_{y}}^{2}\left[{\frac {{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{2}}}-{\frac {{\lambda _{\mu }}^{2}}{{p_{0}}^{3}{p_{0}}^{4}}}-{\frac {{\lambda _{\mu }}^{2}{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{4}}}+{\frac {1}{{p_{0}}^{2}{p_{0}}^{3}}}+{\frac {2{\lambda _{\mu }}^{3}}{{p_{0}}^{2}{p_{0}}^{4}}}\right]\\&-{\frac {1}{{p_{0}}^{1}{p_{0}}^{2}{p_{0}}^{3}{p_{0}}^{4}}}\left[S_{2}+8{p_{y}}^{2}{p_{z}}^{2}+2{p_{y}}^{2}\left[-\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)-\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)-\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)-\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)+2\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{3}\right)-2\left(mc\right)^{2}\right]\right]\end{aligned}}$.

Gl. (8,9)

${\begin{array}{|c|r|c|c|c|c|c|c|c|c|c|}\hline {\begin{array}{c}{\textrm {Reihen-}}\\{\textrm {folge}}\end{array}}&{\begin{array}{c}{\textrm {Reziproker}}\\{\textrm {Nenner}}\end{array}}&{\frac {1}{{{\mathfrak {p}}_{0}}^{3}}}&{\frac {1}{2}}{\frac {({\mathfrak {pg}})}{{p_{0}}^{5}}}&{\frac {1}{4}}{\frac {g^{2}}{p_{0}^{5}}}&{\frac {1}{4}}{\frac {({\mathfrak {pg}})^{2}}{{p_{0}}^{7}}}&{\frac {1}{8}}{\frac {({\mathfrak {pg}})g^{2}}{{p_{0}}^{7}}}&{\frac {({\mathfrak {pg}})^{3}}{8{p_{0}}^{9}}}&{\frac {g^{4}}{16{p_{0}}^{7}}}&{\frac {({\mathfrak {pg}})^{2}g^{2}}{16{p_{0}}^{9}}}&{\frac {({\mathfrak {pg}})^{4}}{16{p_{0}}^{11}}}\\\hline g^{1}g^{2}g^{3}g^{4}&{\frac {1}{N_{1}}}=&1&-2&9&5&-22&-14&30&56&42\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&-6&8&20&-10&-70&32&-28&252\\&{\frac {1}{N_{4}}}=&1&-4&-3&15&24&-56&10&-140&210\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-3&-1&9&8&-28&2&-44&90\\\hline g^{1}g^{2}g^{4}g^{3}&{\frac {1}{N_{1}}}=&1&0&9&3&0&0&30&28&22\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&0&8&8&0&0&32&0&64\\&{\frac {1}{N_{4}}}=&1&-2&-3&7&10&-18&10&-60&66\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-1&-1&5&4&-8&2&-28&42\\\hline g^{1}g^{3}g^{4}g^{2}&{\frac {1}{N_{1}}}=&1&-4&-5&17&48&-80&38&-372&414\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&-12&-4&68&72&-392&44&-840&2332\\&{\frac {1}{N_{4}}}=&1&-6&3&33&-18&-182&-18&28&1030\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-5&-5&25&56&-132&34&-484&738\\\hline g^{1}g^{4}g^{3}g^{2}&{\frac {1}{N_{1}}}=&1&-2&-1&5&6&-14&2&-28&42\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&-6&8&20&-50&-70&-8&252&252\\&{\frac {1}{N_{4}}}=&1&-4&7&15&-48&-56&-6&252&210\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-3&-1&9&8&-28&2&-44&90\\\hline g^{1}g^{4}g^{2}g^{3}&{\frac {1}{N_{1}}}=&1&0&1&3&0&0&-2&-4&22\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&0&-4&8&0&0&12&-60&64\\&{\frac {1}{N_{4}}}=&1&-2&-1&7&2&-18&2&-28&66\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-1&3&5&-4&-8&-6&12&42\\\hline g^{1}g^{3}g^{2}g^{4}&{\frac {1}{N_{1}}}=&1&-4&-3&17&36&-80&26&-312&414\\&{\frac {1}{N_{2}}}+{\frac {1}{N_{3}}}=&2&-12&-16&68&192&-392&144&-1740&2332\\&{\frac {1}{N_{4}}}=&1&-6&-5&33&62&-182&30&-564&1030\\&{\frac {1}{N_{5}}}+{\frac {1}{N_{6}}}=&1&-5&-1&25&24&-132&2&-276&738\\\hline \end{array}}$

Gl. (8,10)

${\textrm {Reihen-}}$ ${\textrm {folge}}$

${\mbox{Zähler}}$

$1$

${\frac {({\mathfrak {pg}})}{{p_{0}}^{2}}}$

${\frac {|g|^{2}}{{p_{0}}^{2}}}$

${\frac {({\mathfrak {pg}})^{2}}{p_{0}^{4}}}$

${\frac {({\mathfrak {pg}})|g|^{2}}{{p_{0}}^{4}}}$

${\frac {({\mathfrak {pg}})^{3}}{{p_{0}}^{6}}}$

${\frac {|g|^{4}}{{p_{0}}^{4}}}$

${\frac {({\mathfrak {pg}})^{2}|g|^{2}}{{p_{0}}^{6}}}$

${\frac {({\mathfrak {pg}})^{4}}{{p_{0}}^{8}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$1$

${\frac {2{p_{y}}^{2}}{{p_{0}}^{2}}}$

${\frac {8{p_{y}}^{2}{p_{z}}^{2}}{{p_{0}}^{4}}}$

$g^{1}g^{2}g^{3}g^{4}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\-8\end{aligned}}$

${\begin{aligned}0\\0\\4\\8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}4\\4\\-4\\-8\end{aligned}}$

${\begin{aligned}2\\2\\2\\2\end{aligned}}$

${\begin{aligned}2\\2\\2\\4\end{aligned}}$

${\begin{aligned}0\\0\\-4\\-6\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-4\end{aligned}}$

${\begin{aligned}-8\\-8\\8\\14\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-4\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}-4\\-4\\12\\18\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-4\end{aligned}}$

${\begin{aligned}4\\4\\4\\+8\end{aligned}}$

${\begin{aligned}16\\16\\-16\\-26\end{aligned}}$

${\begin{aligned}8\\8\\8\\8\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}0\\0\\4\\{\tfrac {11}{2}}\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}10\\10\\10\\19\end{aligned}}$

${\begin{aligned}16\\16\\-32\\-47\end{aligned}}$

${\begin{aligned}12\\12\\12\\12\end{aligned}}$

${\begin{aligned}-8\\-8\\-8\\-{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}-32\\-32\\+32\\{\tfrac {99}{2}}\end{aligned}}$

${\begin{aligned}-16\\-16\\-16\\-16\end{aligned}}$

$g^{1}g^{2}g^{4}g^{3}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\-8\end{aligned}}$

${\begin{aligned}0\\0\\4\\8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\4\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}-2\\-2\\2\\4\end{aligned}}$

${\begin{aligned}0\\0\\-4\\-6\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}2\\2\\-2\\-4\end{aligned}}$

${\begin{aligned}0\\0\\8\\14\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-2\end{aligned}}$

${\begin{aligned}0\\0\\4\\0\end{aligned}}$

${\begin{aligned}0\\0\\-6\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\-4\\0\end{aligned}}$

${\begin{aligned}0\\0\\10\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}2\\2\\-2\\-{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}0\\0\\4\\{\tfrac {11}{2}}\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}-6\\-6\\10\\19\end{aligned}}$

${\begin{aligned}0\\0\\-24\\-39\end{aligned}}$

${\begin{aligned}6\\6\\6\\6\end{aligned}}$

${\begin{aligned}4\\4\\-8\\-{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}0\\0\\24\\{\tfrac {83}{2}}\end{aligned}}$

${\begin{aligned}-6\\-6\\-6\\-6\end{aligned}}$

$g^{1}g^{3}g^{4}g^{2}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\-8\end{aligned}}$

${\begin{aligned}4\\0\\0\\8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}-12\\0\\0\\-16\end{aligned}}$

${\begin{aligned}4\\4\\4\\4\end{aligned}}$

${\begin{aligned}2\\-2\\-2\\4\end{aligned}}$

${\begin{aligned}-12\\0\\0\\-14\end{aligned}}$

${\begin{aligned}3\\3\\3\\3\end{aligned}}$

${\begin{aligned}-2\\2\\2\\-4\end{aligned}}$

${\begin{aligned}40\\0\\0\\46\end{aligned}}$

${\begin{aligned}-14\\-14\\-14\\-14\end{aligned}}$

${\begin{aligned}-12\\8\\8\\-16\end{aligned}}$

${\begin{aligned}78\\0\\0\\84\end{aligned}}$

${\begin{aligned}-22\\-22\\-22\\-22\end{aligned}}$

${\begin{aligned}12\\-8\\-8\\16\end{aligned}}$

${\begin{aligned}-138\\0\\0\\-148\end{aligned}}$

${\begin{aligned}48\\48\\48\\48\end{aligned}}$

${\begin{aligned}-10\\6\\6\\-{\tfrac {23}{2}}\end{aligned}}$

${\begin{aligned}38\\0\\0\\{\tfrac {79}{2}}\end{aligned}}$

${\begin{aligned}-9\\-9\\-9\\-9\end{aligned}}$

${\begin{aligned}66\\-34\\-34\\75\end{aligned}}$

${\begin{aligned}-402\\0\\0\\-417\end{aligned}}$

${\begin{aligned}118\\118\\118\\118\end{aligned}}$

${\begin{aligned}-56\\28\\28\\-{\tfrac {127}{2}}\end{aligned}}$

${\begin{aligned}488\\0\\0\\{\tfrac {1011}{2}}\end{aligned}}$

${\begin{aligned}-166\\-166\\-166\\-166\end{aligned}}$

$g^{1}g^{4}g^{3}g^{2}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\-8\end{aligned}}$

${\begin{aligned}4\\0\\0\\8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}2\\2\\2\\2\end{aligned}}$

${\begin{aligned}2\\2\\2\\4\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-6\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-4\end{aligned}}$

${\begin{aligned}8\\8\\8\\14\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-4\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}12\\12\\12\\18\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-4\end{aligned}}$

${\begin{aligned}4\\4\\4\\8\end{aligned}}$

${\begin{aligned}-16\\-16\\-16\\-26\end{aligned}}$

${\begin{aligned}8\\8\\8\\8\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}4\\4\\4\\{\tfrac {11}{2}}\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}10\\10\\10\\19\end{aligned}}$

${\begin{aligned}-32\\-32\\-32\\-47\end{aligned}}$

${\begin{aligned}12\\12\\12\\12\end{aligned}}$

${\begin{aligned}-8\\-8\\-8\\-{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}32\\32\\32\\{\tfrac {99}{2}}\end{aligned}}$

${\begin{aligned}-16\\-16\\-16\\-16\end{aligned}}$

$g^{1}g^{4}g^{2}g^{3}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\8\end{aligned}}$

${\begin{aligned}0\\4\\0\\-8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\-4\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}2\\2\\-2\\-4\end{aligned}}$

${\begin{aligned}-4\\-4\\0\\2\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}-2\\-2\\2\\4\end{aligned}}$

${\begin{aligned}4\\4\\-4\\-10\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-2\end{aligned}}$

${\begin{aligned}0\\0\\-4\\0\end{aligned}}$

${\begin{aligned}0\\0\\6\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\4\\0\end{aligned}}$

${\begin{aligned}0\\0\\-10\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}-2\\-2\\2\\{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}4\\4\\0\\-{\tfrac {3}{2}}\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}6\\6\\-10\\-19\end{aligned}}$

${\begin{aligned}-16\\-16\\8\\23\end{aligned}}$

${\begin{aligned}6\\6\\6\\6\end{aligned}}$

${\begin{aligned}-4\\-4\\8\\{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}12\\12\\-12\\-{\tfrac {59}{2}}\end{aligned}}$

${\begin{aligned}-6\\-6\\-6\\-6\end{aligned}}$

$g^{1}g^{3}g^{2}g^{4}$

${\begin{aligned}z_{1}=\\z_{2}=z_{3}=\\z_{4}=\\z_{5}=z_{6}=\end{aligned}}$

${\begin{aligned}0\\0\\0\\8\end{aligned}}$

${\begin{aligned}0\\4\\0\\-8\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}4\\-8\\0\\16\end{aligned}}$

${\begin{aligned}4\\4\\4\\4\end{aligned}}$

${\begin{aligned}-2\\2\\2\\-4\end{aligned}}$

${\begin{aligned}4\\-8\\-4\\10\end{aligned}}$

${\begin{aligned}3\\3\\3\\3\end{aligned}}$

${\begin{aligned}2\\-2\\-2\\4\end{aligned}}$

${\begin{aligned}-20\\20\\4\\-42\end{aligned}}$

${\begin{aligned}-14\\-14\\-14\\-14\end{aligned}}$

${\begin{aligned}12\\-8\\-8\\16\end{aligned}}$

${\begin{aligned}-38\\40\\24\\-60\end{aligned}}$

${\begin{aligned}-22\\-22\\-22\\-22\end{aligned}}$

${\begin{aligned}-12\\8\\8\\-16\end{aligned}}$

${\begin{aligned}82\\-56\\-24\\124\end{aligned}}$

${\begin{aligned}48\\48\\48\\48\end{aligned}}$

${\begin{aligned}10\\-6\\-6\\{\tfrac {23}{2}}\end{aligned}}$

${\begin{aligned}-18\\20\\16\\-{\tfrac {47}{2}}\end{aligned}}$

${\begin{aligned}-9\\-9\\-9\\-9\end{aligned}}$

${\begin{aligned}-66\\34\\34\\-75\end{aligned}}$

${\begin{aligned}230\\-172\\-124\\293\end{aligned}}$

${\begin{aligned}118\\118\\118\\118\end{aligned}}$

${\begin{aligned}56\\-28\\-28\\{\tfrac {127}{2}}\end{aligned}}$

${\begin{aligned}-316\\172\\108\\-{\tfrac {795}{2}}\end{aligned}}$

${\begin{aligned}-166\\-166\\-166\\-166\end{aligned}}$

Für die Reihenfolge: $g^{1}g^{4}g^{2}g^{3}$ und $g^{1}g^{3}g^{2}g^{4}$

${\begin{aligned}Z_{\mu }&=-S_{1}+2{p_{y}}^{2}\left[-{\frac {{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{2}}}+{\frac {{\lambda _{\mu }}^{2}}{{p_{0}}^{3}{p_{0}}^{4}}}+{\frac {{\lambda _{\mu }}^{2}{\lambda _{\mu }}^{3}}{{p_{0}}^{1}{p_{0}}^{4}}}-{\frac {1}{{p_{0}}^{2}{p_{0}}^{3}}}+{\frac {2{\lambda _{\mu }}^{2}}{{p_{0}}^{1}{p_{0}}^{3}}}-{\frac {2{\lambda _{\mu }}^{3}}{{p_{0}}^{2}{p_{0}}^{4}}}\right]\\&-{\frac {1}{{p_{0}}^{1}{p_{0}}^{2}{p_{0}}^{3}{p_{0}}^{4}}}\left[-S_{2}+2{p_{y}}^{2}\left[\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)+\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)+\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)+\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)-2\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{3}\right)-2\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)\right]\right]\end{aligned}}$

Darin bedeuten $S_{1}$, $S_{2}$ die Abkürzung:

${\begin{aligned}S_{1}&={\lambda _{\mu }}^{2}{\lambda _{\mu }}^{3}-{\lambda _{\mu }}^{3}{\frac {\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)+(mc)^{2}}{{p_{0}}^{1}{p_{0}}^{2}}}+{\lambda _{\mu }}^{2}{\frac {\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)+(mc)^{2}}{{p_{0}}^{3}{p_{0}}^{4}}}-{\lambda _{\mu }}^{3}{\frac {\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{4}\right)+(mc)^{2}}{{p_{0}}^{2}{p_{0}}^{4}}}\\&+{\lambda _{\mu }}^{2}{\lambda _{\mu }}^{3}{\frac {\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)+(mc)^{2}}{{p_{0}}^{1}{p_{0}}^{4}}}-1\cdot {\frac {\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)+(mc)^{2}}{{p_{0}}^{2}{p_{0}}^{3}}}+{\lambda _{\mu }}^{2}{\frac {\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{3}\right)+(mc)^{2}}{{p_{0}}^{1}{p_{0}}^{3}}}\end{aligned}}$,

$S_{2}=\left[{\begin{aligned}&\left[\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)+(mc)^{2}\right]\left[\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)+(mc)^{2}\right]+\left[\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)+(mc)^{2}\right]\left[\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)+(mc)^{2}\right]\\-&\left[\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{3}\right)+(mc)^{2}\right]\left[\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{4}\right)+(mc)^{2}\right]\end{aligned}}\right]$.

Diese Ausdrücke werden bei weiterer Spezialisierung auf parallele Impulse, wie man durch Einsetzen von (8‚8‚ $\delta$) und Entwicklung nach $g/mc$ bis zur 4. Ordnung findet:

Vgl. Gl. (8,10).

Um die Zähler (5,15) durch die Nenner (5,14) zu dividieren, über die 6 Übergangswege $\mu$ und die 24 Reihenfolgen (8,8, $\alpha$) zu summieren, muß man die Spalten der Tab. (8,10) mit den entsprechenden Spalten der Tab. (8,9) und mit dem Faktor 4 multiplizieren. Man erhält dann im Glied 4. Ordnung in $g/mc$ nach Mittelung über die Positronenrichtung ${\mathfrak {p}}$: [vgl. § 9,7]

Gl. (8,15)

$1$

${\frac {({\mathfrak {pg}})}{p_{0}^{2}}}$

${\frac {|g|^{2}}{p_{0}^{2}}}$

${\frac {({\mathfrak {pg}})^{2}}{p_{0}^{4}}}$

${\frac {({\mathfrak {pg}})(g)^{2}}{p_{0}^{4}}}$

${\frac {({\mathfrak {pg}})^{3}}{p_{0}^{6}}}$

${\frac {|g|^{4}}{p_{0}^{2}}}$

${\frac {({\mathfrak {pg}})^{2}|g|^{2}}{p_{0}^{6}}}$

${\frac {({\mathfrak {pg}})^{4}}{p_{0}^{8}}}$

${\textrm {Reihen-}}$ ${\textrm {folge}}$

${\mbox{Zähler}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

$1$

${\frac {2p_{y}^{2}}{p_{0}^{2}}}$

${\frac {8p_{y}^{4}}{p_{0}^{4}}}$

${\begin{aligned}g^{1}g^{2}g^{3}g^{4}\\g^{1}g^{4}g^{3}g^{2}\end{aligned}}$

${\begin{aligned}-z_{1}&=\\-z_{2}=-z_{3}&=\\-z_{4}&=\\-z_{5}=-&z_{6}\end{aligned}}$

${\begin{aligned}0\\0\\0\\8\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}4\\4\\4\\8\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-2\end{aligned}}$

${\begin{aligned}-2\\-2\\-2\\-4\end{aligned}}$

${\begin{aligned}4\\4\\4\\6\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}2\\2\\2\\4\end{aligned}}$

${\begin{aligned}-8\\-8\\-8\\-14\end{aligned}}$

${\begin{aligned}4\\4\\4\\4\end{aligned}}$

${\begin{aligned}4\\4\\4\\8\end{aligned}}$

${\begin{aligned}-12\\-12\\-12\\-18\end{aligned}}$

${\begin{aligned}4\\4\\4\\4\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}16\\16\\16\\26\end{aligned}}$

${\begin{aligned}-8\\-8\\-8\\-8\end{aligned}}$

${\begin{aligned}2\\2\\2\\{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-{\tfrac {11}{2}}\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}-10\\-10\\-10\\-19\end{aligned}}$

${\begin{aligned}32\\32\\32\\47\end{aligned}}$

${\begin{aligned}-12\\-12\\-12\\-12\end{aligned}}$

${\begin{aligned}8\\8\\8\\{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}-32\\-32\\-32\\{\tfrac {99}{2}}\end{aligned}}$

${\begin{aligned}16\\16\\16\\16\end{aligned}}$

${\begin{aligned}g^{1}g^{2}g^{4}g^{3}\\g^{1}g^{4}g^{2}g^{3}\end{aligned}}$

${\begin{aligned}-z_{1}&=\\-z_{2}=-&z_{3}\\-z_{4}&=\\-z_{5}=-&z_{6}\end{aligned}}$

${\begin{aligned}0\\0\\0\\8\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\-4\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}2\\2\\-2\\-4\end{aligned}}$

${\begin{aligned}4\\4\\4\\6\end{aligned}}$

${\begin{aligned}-1\\-1\\-1\\-1\end{aligned}}$

${\begin{aligned}-2\\-2\\2\\4\end{aligned}}$

${\begin{aligned}-8\\-8\\-8\\-14\end{aligned}}$

${\begin{aligned}2\\2\\2\\2\end{aligned}}$

${\begin{aligned}0\\0\\-4\\0\end{aligned}}$

${\begin{aligned}0\\0\\6\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}0\\0\\4\\0\end{aligned}}$

${\begin{aligned}0\\0\\-10\\0\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}-2\\-2\\2\\{\tfrac {7}{2}}\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-{\tfrac {11}{2}}\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}6\\6\\-10\\-19\end{aligned}}$

${\begin{aligned}24\\24\\24\\39\end{aligned}}$

${\begin{aligned}-6\\-6\\-6\\-6\end{aligned}}$

${\begin{aligned}-4\\-4\\8\\{\tfrac {31}{2}}\end{aligned}}$

${\begin{aligned}-24\\-24\\-24\\-{\tfrac {83}{2}}\end{aligned}}$

${\begin{aligned}6\\6\\6\\6\end{aligned}}$

${\begin{aligned}g^{1}g^{3}g^{4}g^{2}\\g^{1}g^{3}g^{2}g^{4}\end{aligned}}$

${\begin{aligned}-z_{1}&=\\-z_{2}=-&z_{3}\\-z_{4}&=\\-z_{5}=-z_{6}&=\end{aligned}}$

${\begin{aligned}0\\0\\0\\8\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-8\end{aligned}}$

${\begin{aligned}1\\1\\1\\1\end{aligned}}$

${\begin{aligned}0\\0\\0\\0\end{aligned}}$

${\begin{aligned}12\\8\\8\\16\end{aligned}}$

${\begin{aligned}-4\\-4\\-4\\-4\end{aligned}}$

${\begin{aligned}-2\\2\\2\\-4\end{aligned}}$

${\begin{aligned}12\\8\\8\\14\end{aligned}}$

${\begin{aligned}-3\\-3\\-3\\-3\end{aligned}}$

${\begin{aligned}2\\-2\\-2\\4\end{aligned}}$

${\begin{aligned}-40\\-24\\-24\\-46\end{aligned}}$

${\begin{aligned}14\\14\\14\\14\end{aligned}}$

${\begin{aligned}12\\-8\\-8\\16\end{aligned}}$

${\begin{aligned}-78\\-48\\-48\\-84\end{aligned}}$

${\begin{aligned}22\\22\\22\\22\end{aligned}}$

${\begin{aligned}-12\\8\\8\\-16\end{aligned}}$

${\begin{aligned}138\\80\\80\\148\end{aligned}}$

${\begin{aligned}-48\\-48\\-48\\-48\end{aligned}}$

${\begin{aligned}10\\-6\\-6\\{\tfrac {23}{2}}\end{aligned}}$

${\begin{aligned}-38\\-24\\-24\\-{\tfrac {79}{2}}\end{aligned}}$

${\begin{aligned}9\\9\\9\\9\end{aligned}}$

${\begin{aligned}-66\\+34\\+34\\-75\end{aligned}}$

${\begin{aligned}402\\240\\240\\417\end{aligned}}$

${\begin{aligned}-118\\-118\\-118\\-118\end{aligned}}$

${\begin{aligned}56\\-28\\-28\\{\tfrac {127}{2}}\end{aligned}}$

${\begin{aligned}-488\\-280\\-280\\-{\tfrac {1011}{2}}\end{aligned}}$

${\begin{aligned}116\\116\\116\\116\end{aligned}}$

(8,11)

$\left\lbrace \sum _{\mathrm {Perm} }\sum _{\mu }{\frac {{\bar {Z}}_{\mu }}{N_{\mu }}}={\frac {4|g|4}{p_{0}^{7}}}\cdot \left[-63+1002{\frac {p^{2}}{3p_{0}^{2}}}-7734{\frac {p^{4}}{3\cdot 5p_{0}^{4}}}-315{\frac {p^{4}}{5p_{0}^{4}}}+22800{\frac {p^{6}}{2\cdot 5\cdot 7p_{0}^{6}}}+7524{\frac {p^{6}}{5\cdot 7p_{0}^{6}}}-47606{\frac {p^{8}}{5\cdot 7\cdot 9p_{0}^{8}}}\right]\right.$

und nach Integration^[13] $4\pi \int p^{2}dp$ über die Positronenenergie $p_{0}$:

(8,12)

$\left\lbrace C\int d{\mathfrak {p}}\sum _{\mathrm {Perm} }\sum _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}=C\cdot 4\pi \cdot 4\cdot 2\left({\frac {g}{mc}}\right)^{4}\cdot \left[-{\frac {63}{3\cdot 5}}+{\frac {1002}{3\cdot 5\cdot 7}}-{\frac {7734}{3\cdot 5\cdot 7\cdot 9}}-{\frac {315}{5\cdot 7\cdot 9}}+{\frac {22800}{3\cdot 5\cdot 7\cdot 9\cdot 11}}+{\frac {7524}{5\cdot 7\cdot 9\cdot 11}}-{\frac {47606}{5\cdot 7\cdot 9\cdot 11\cdot 13}}\right]\cdot \right.$

(8,13)

$=4\pi \cdot 4\cdot 2\left(-{\frac {8}{3\cdot 5}}\right)\cdot \left({\frac {g}{mc}}\right)^{4}\cdot C=H_{\bot }^{4}$.

Ebenso verläuft die Rechnung für den Spezialfall (8,2 b): Indem man im Zähler (5,15) für parallele Polarisationen (8,8, $\gamma$) die Spur bildet, erhält man:

(8,14)

$\left\{{\begin{aligned}Z_{\mu }=S_{1}+2p_{y}^{2}\left[{\frac {\lambda _{\mu }^{3}}{p_{0}^{1}p_{0}^{2}}}-{\frac {\lambda _{\mu }^{2}}{p_{0}^{3}p_{0}^{4}}}-{\frac {\lambda _{\mu }^{2}\lambda _{\mu }^{3}}{p_{0}^{1}p_{0}^{4}}}+{\frac {1}{p_{0}^{2}p_{0}^{3}}}\right]-{\frac {1}{p_{0}^{1}p_{0}^{2}p_{0}^{3}p_{0}^{4}}}&\left[S_{2}+8p_{y}^{4}-2p_{y}^{2}\left[\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{2}\right)+\left({\mathfrak {p}}^{3}{\mathfrak {p}}^{4}\right)+\left({\mathfrak {p}}^{2}{\mathfrak {p}}^{3}\right)+\left({\mathfrak {p}}^{1}{\mathfrak {p}}^{4}\right)+4\left(mc\right)^{4}\right]\right]\\&(S_{1},S_{2}\ {\text{vgl. S. 432).}}\end{aligned}}\right.$

Und dies wird, wenn man zur weiteren Spezialisierung auf parallele Impulse (8,8, $\delta$) einsetzt und nach Lichtquantenenergien $g/mc$, entwickelt:

Vgl. Gl. (8,15).

Multiplikation dieser Zähler (8,15) mit den entsprechenden Nennern (8,9), Addition über die 6 Reihenfolgen (8,8) und die 6 Fälle $\mu$, Multiplikation mit 4 und Mittelung über die Winkel von ${\mathfrak {p}}$ ergibt im Glied 4. Ordnung der Entwicklung nach Lichtfrequenzen:

(8,16)

$\left\lbrace -{\frac {1}{2}}\sum _{\mathrm {Perm} }\sum _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}=4{\frac {|g|^{4}}{p_{0}^{7}}}\left[{\frac {41}{2}}-917{\frac {p^{2}}{3p_{0}^{2}}}+{\frac {2379}{2}}{\frac {p^{4}}{5p_{0}^{4}}}+8400{\frac {p^{4}}{3\cdot 5\cdot p_{0}^{4}}}-26316{\frac {p^{6}}{5\cdot 7p_{0}^{6}}}+23803{\frac {p^{8}}{3\cdot 5\cdot 7p_{0}^{8}}}\right]\right.$

und dies wird nach Integration über $p$:

(8,17)

$C\int \mathrm {d} p\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}=C\cdot 4\pi (-2)\cdot 4\cdot 2\left({\frac {g}{mc}}\right)^{4}\left[{\frac {41}{2\cdot 3\cdot 5}}-{\frac {917}{3\cdot 5\cdot 7}}+{\frac {2379}{2\cdot 5\cdot 7\cdot 9}}\;+{\frac {8400}{3\cdot 5\cdot 7\cdot 9}}-{\frac {26316}{5\cdot 7\cdot 9\cdot 11}}+{\frac {23803}{3\cdot 5\cdot 7\cdot 11\cdot 13}}\right]$

(8,18)

$=-4\pi \cdot 16\cdot \left(-{\frac {32}{5\cdot 9}}\right)\left({\frac {g}{mc}}\right)^{4}\cdot C=H_{\Vert }^{4}.$

Nun sind die Matrixelemente der Diracschen Theorie (8,13; 8,18) in ihren Gliedern 4. Ordnung und die Matrixelemente der Lichtquantenwechselwirkung (8,6; 8,7) für die beiden betrachteten Übergänge (8,2 a, b) ausgerechnet.

Ihre Gleichsetzung (8,3):

${\begin{aligned}{\textrm {a)}}\ &\bot &:&&&(32\alpha &-8\beta )|g|^{4}&D{\frac {\hbar c}{e^{2}}}{\frac {1}{E_{0}^{2}}}={\frac {-4\pi \cdot 6\cdot 32}{5\cdot 9}}\left({\frac {g}{mc}}\right)^{4}C\\{\textrm {b)}}\ &\Vert &:&&&(64\alpha &)|g|^{4}&D{\frac {\hbar c}{e^{2}}}{\frac {1}{E_{0}^{2}}}+{\frac {4\pi \cdot 16\cdot 32}{5\cdot 9}}\left({\frac {g}{mc}}\right)^{4}C\end{aligned}}$

bestimmt die beiden Konstanten $\alpha ,\beta$ zu

(8,19)

${\begin{array}{|ccc|}\hline &&\\&{\begin{aligned}\alpha =-{\frac {1}{360\pi ^{2}}}\\\beta =-{\frac {7}{360\pi ^{2}}}\end{aligned}}&\\&&\\\hline \end{array}}$

Die Einfachheit des Resultate legt die Vermutung nahe, daß es möglich sein muß, auf einem einfacheren Wege zu dem hier abgeleiteten Ergebnis zu kommen. Dieser einfachere Weg wird in einer inzwischen erschienenen Arbeit beschritten^[14]

§ 9. Bestätigung des Verfahrens

Im vorigen Paragraphen wurden zwei Konstanten $\alpha ,\beta$ so bestimmt, daß das Diracsche Matrixelement $H_{in}^{4}$ für Streuung von Licht an Licht (im Gliede 4. Ordnung der Entwicklung nach Lichtfrequenzen $g^{i}/mc$) in zwei speziellen Fällen (8,2a‚ b) durch den Ausdruck (2,21):

(9,1)

${\frac {\hbar c}{e^{2}}}{\frac {1}{E_{0}^{2}}}\int \left[\alpha ({\mathfrak {BD}})^{2}+\beta \left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}\right]dV$

dargestellt wird.

Die Möglichkeit dieser Bestimmung beruht nur auf der Tatsache, daß beide Ausdrücke zu den betrachteten 2 Übergängen ein nichtverschwindendes Matrixelement geben.

Die Behauptung aber, auf welche es ankommt, daß (9,1) für alle Fälle (bis einschließlich zur 4. Ordnung in $g^{i}/mc$) die Streuung von Licht an Licht vollständig darstellt, enthält die Voraussetzung, daß es überhaupt einen korrespondenzmäßigen Ausdruck für die Streuung von Licht an Licht gibt, daß (wegen dessen Eichinvarianz) die Entwicklungsglieder 1., 2. und 3. Ordnung des Diracschen Matrixelements nach Lichtfrequenzen immer verschwinden und daß (wegen seiner Lorentzinvarianz) das Glied 4. Ordnung dieser Entwicklung des Diracschen Matrixelements von der Form (9,1) ist.

Diese Voraussetzung und die daraus folgende Behauptung, daß wir auch ohne Spezialisierung bei Durchrechnung des Diracschen Matrixelements für 4 beliebige Lichtquanten das Resultat (9,1) erhalten hätten, soll jetzt durch einige numerische Rechnungen kontrolliert werden.

Wir berechnen in der Entwicklung des Diracschen Matrixelements nach Lichtfrequenzen:

1. die 1. Näherung allgemein,
2. die 2. Näherung unter einer einschränkenden Voraussetzung über die Polarisationen,
3. die 3. Näherung für die zwei oben behandelten Spezialfalle a) und b) und bestimmen
4. die Konstante $\alpha$ noch einmal auf einem vom obigen ganz unabhängigen Wege.

Wenn 1., 2. und 3. das Resultat 0, und 4. wieder das Resultat $\alpha =-{\tfrac {1}{360\pi ^{2}}}$ ergeben, können wir darin für unser Verfahren eine direkte Bestätigung sehen.

1. Das Glied 1. Ordnung des Diracschen Matrixelements in der Entwicklung nach $g^{i}/mc$ muß immer verschwinden: denn es ist linear in den Impulsen und Energien der Lichtquanten als Glied 1. Ordnung, symmetrisch in den 4 Lichtquanten wegen der Summation über die Lichtquantenpermutationen, also 0 infolge des Erhaltungssatzes $\sum \limits _{\textrm {Perm}}g^{1}=0$, $\sum \limits _{\textrm {Perm}}{\mathfrak {g}}^{1}=0$ für Energie und Impuls.

2. Das Glied 2. Ordnung in $g^{i}/mc$ des Diracschen Matrixelements soll in dem speziellen Fall ausgerechnet werden, in dem alle 4 Lichtquanten parallele Polarisationen, aber beliebige komplanare Impulse ${\mathfrak {g}}^{1},{\mathfrak {g}}^{2},{\mathfrak {g}}^{3},{\mathfrak {g}}^{4}$ haben.

In diesem Fall erhält man durch Entwicklung des Zählers $Z_{\mu }$ (5,15), welcher die Produkte der 4 gewöhnlichen Matrixelemente der Teilprozesse enthält, bis zur 2. Ordnung in $g^{i}/cm$: (Statt für 6 Übergangsfälle $\mu =1\dots 6$ von denen nur 4 verschieden sind, 4 Gleichungen einzeln aufzuschreiben, sind sie durch Spalten ${\begin{array}{|c|}Z_{1}\\Z_{2}=Z_{3}\\Z_{4}\\Z_{5}=Z_{6}\end{array}}$ von je 4 Zahlen in einer Gleichung zusammengefaßt):

(9,2)

$\left\{{\begin{aligned}{\begin{array}{|c|}Z_{1}\\Z_{2}=Z_{3}\\Z_{4}\\Z_{5}=Z_{6}\end{array}}=&-8{\begin{array}{|c|}0\\0\\0\\1\end{array}}+8{\frac {p_{y}^{2}}{p_{0}^{2}}}{\begin{array}{|c|}1\\1\\1\\1\end{array}}-80{\frac {p_{y}^{4}}{p_{0}^{4}}}{\begin{array}{|c|}1\\1\\1\\1\end{array}}\\&-4{\frac {p_{y}^{2}}{p_{0}^{4}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|c|}3\\2\\1\\4\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|c|}2\\1\\1\\2\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|c|}-1\\-1\\-2\\-2\end{array}}\right]\\&+{\frac {8p_{y}^{4}}{p_{0}^{4}}}\left({\mathfrak {p}},2{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}-{\mathfrak {g}}^{4}\right){\begin{array}{|c|}1\\1\\1\\1\end{array}}\\&-{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)}{6p_{0}^{2}}}\left[4{\begin{array}{|r|}-1\\-1\\-1\\6\end{array}}+8{\frac {p_{y}^{2}}{p_{0}^{2}}}{\begin{array}{|r|}10\\8\\8\\13\end{array}}+80{\frac {p_{y}^{4}}{p_{0}^{4}}}{\begin{array}{|r|}-1\\-1\\-1\\-1\end{array}}\right]\\&-{\frac {\left({\mathfrak {pg}}^{1}\right)^{2}}{6p_{0}^{4}}}\left[4{\begin{array}{|r|}1\\-1\\1\\6\end{array}}+8{\frac {p_{y}^{2}}{p_{0}^{2}}}{\begin{array}{|r|}-28\\-20\\-20\\-37\end{array}}+320{\begin{array}{|c|}1\\1\\1\\1\end{array}}\right].\end{aligned}}\right.$

Darin ist im Gliede 2. Ordnung schon über die 24 Permutationen der Lichtquanten gemittelt unter Beachtung der aus dem Erhaltungssatz folgenden Relationen:

(9,3)

$\ldots =\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)=\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{2}\right)=-3\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)=-3\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{3}\right)=\ldots$

Die Entwicklung der reziproken Nenner $1/N_{\mu }$ (5,14), welche Energiedifferenzen der Zwischenzustände zum Anfangszustand darstellen, bis zum selben Grade wird (in der obigen Bezeichnungsweise);

(9,4)

${\begin{array}{|c|}N_{1}^{-1}\\N_{2}^{-1}+N_{3}^{-1}\\N_{4}^{-1}\\N_{5}^{-1}+N_{6}^{-1}\end{array}}={\frac {1}{{p_{0}}^{3}}}{\begin{array}{|c|}1\\2\\1\\1\end{array}}+{\frac {1}{2{p_{0}}^{5}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|c|}-2\\-6\\-4\\-3\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|c|}-1\\-3\\-1\\-1\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|c|}1\\3\\1\\1\end{array}}\right]+{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)}{12{p_{0}}^{5}}}{\begin{array}{|r|}5\\0\\-1\\-3\end{array}}+{\frac {\left({\mathfrak {pg}}^{1}\right)^{2}}{2{p_{0}}^{7}}}{\begin{array}{|r|}25\\90\\55\\39\end{array}},$

wobei ebenfalls im höchsten Gliede schon über die Permutationen der Lichtquanten gemittelt wurde.

Multiplikation dieser Zähler (9,2) und reziproken Nenner (9,4) ergibt im Gliede 2. Ordnung in $g^{i}/mc$, nach Summation über die 6 Übergangsfälle $\mu =1\ldots 6$, Winkelmittlung über ${\mathfrak {p}}$ und Summation über die Permutationen der Lichtquanten unter Berücksichtigung von (9,3):

$\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {\overline {Z_{\mu }}}{N_{\mu }}}=-\sum \limits _{\textrm {Perm}}{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)}{{p_{0}}^{5}}}\left[-36+{\frac {564}{3}}{\frac {p^{2}}{{p_{0}}^{2}}}-{\frac {3876}{3\cdot 5}}{\frac {p^{4}}{{p_{0}}^{4}}}+{\frac {3564}{5\cdot 7}}{\frac {p^{6}}{{p_{0}}^{6}}}\right]$

und nach Integration^[15] über $p$:

${\begin{aligned}\int d{\mathfrak {p}}\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}&=-4\pi \sum \limits _{\textrm {Perm}}\left({\frac {g^{1}}{mc}}\right)^{2}\left[-{\frac {36}{3}}+{\frac {564}{3\cdot 5}}-{\frac {3876}{3\cdot 5\cdot 7}}+{\frac {3564}{5\cdot 7\cdot 9}}\right]\\&=0.\end{aligned}}$

Tatsächlich verschwindet also bei beliebigen Impulsen das Glied 2. Ordnung in $g^{i}/mc$ des Diracschen Matrixelements für Streuung von Licht an Licht paralleler Polarisationen.

Die entsprechende 2. Ordnung nichtparalleler Polarisation soll nur am oben behandelten ganz speziellen Fall (8,2b) senkrechter Polarisation und paralleler Impulse gleichen Betrags untersucht werden.

Hier erhält man für das Glied 2. Ordnung des Diracschen Matrixelements, wenn man die im § 6 berechneten Spalten der Zähler (8,15) mit den Spalten der reziproken Nenner (8,9) multipliziert, die zu Gliedern 2. Ordnung in $g^{i}/mc$ führen, und über die Positronenrichtung ${\mathfrak {p}}$ mittelt:

$\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {\overline {Z_{\mu }}}{N_{\mu }}}=4{\frac {|g|^{2}}{{p_{0}}^{5}}}\left[44-{\frac {332}{3}}{\frac {p^{2}}{{p_{0}}^{2}}}-{\frac {1180}{3\cdot 5}}{\frac {p^{4}}{{p_{0}}^{4}}}-{\frac {3564}{3\cdot 5\cdot 7}}{\frac {p^{6}}{{p_{0}}^{6}}}\right]$

und dies wird nach Integration über die Positronenenergie $p_{0}$:

${\begin{aligned}\int d{\mathfrak {p}}\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {Z_{\mu }}{N_{\mu }}}&=4\pi \cdot 4\left({\frac {g}{mc}}\right)^{2}\left[{\frac {44}{3}}-{\frac {332}{3\cdot 5}}+{\frac {1180}{3\cdot 5\cdot 7}}-{\frac {3564}{3\cdot 5\cdot 7\cdot 9}}\right]\\&=0\end{aligned}}$

in Übereinstimmung mit unserer allgemeinen Behauptung.

3. Das Verschwinden der Glieder Ordnung in der Entwicklung des Diracschen Matrixelements nach Lichtfrequenzen soll ebenfalls nur in den beiden speziellen oben behandelten Fällen (8,2 a, b) paralleler gleich großer Impulse und paralleler und senkrechter Polarisationen nachgeprüft werden. Hier haben wir es aber schon bestätigt. Denn nach S. 430 fallen alle ungeraden Potenzen aus Lichtquantenimpulsen und -Energien fort, weil über die Permutationen der z. T. gleichen, z. T. entgegengesetzten Lichtquanten summiert wird.

4. Die Konstante $\alpha$, welche für die Streuung von Licht an Licht paralleler Polarisation maßgebend ist, soll nun auf einem neuen Wege nochmals berechnet werden. Statt, wie wir es oben taten, in einem speziellen Fall (8,2 b) gleicher bzw. entgegengesetzt gleicher Impulse die Matrixelemente (5,13) der Diracschen Theorie und der Feldfunktion (8,4) zu vergleichen, betrachten wir jetzt den allgemeinen Fall beliebiger Impulse (bei parallelen Polarisationen), beschränken uns aber auf den Vergleich eines der Glieder in (8,4), die zu dem betrachteten Übergang beitragen.

Das Matrixelement von:

$\alpha {\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\int \left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}dV$

enthält nach (8,4) für einen Übergang $\Vert$ Polarisationen der drei Glieder:

(9,5)

$D\cdot \alpha \cdot {\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\sum \limits _{\textrm {Perm}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)-2\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}+g^{1}g^{2}g^{3}g^{4}\right]$.

Wir greifen das mittlere Glied heraus und bestimmen die Konstante $\alpha$ durch Vergleich dieses Glieds

(9,5a)

$\alpha D{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}(-2)\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}$

mit dem entsprechenden Glied des Diracschen Matrixelements, das wir nun berechnen.

Das Matrixelement $H_{in}^{4}$ der Diracschen Theorie besteht (im Gliede 4. Ordnung der Entwicklung nach $g^{i}/mc$) aus symmetrischen Formen 4. Grades in den vier Lichtquantenimpulsen und Energien. Wegen der Erhaltungssätze sind diese aber nicht unabhängig, vielmehr lassen sie sich alle aus den vier Formen

$\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right),\quad \sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4},\quad \sum \limits _{\textrm {Perm}}g^{1}g^{2}g^{3}g^{4},\quad \sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{2}\right)$

linear zusammensetzen, die ihrerseits linear unabhängig sind.

Wie eine einfache Anwendung der Erhaltungssätze:

$\sum \limits _{\textrm {Perm}}{\mathfrak {g}}^{1}=0,\quad \sum \limits _{\textrm {Perm}}g^{1}=0$

zeigt, lauten diese linearen Beziehungen zwischen den verschiedenen Gliedern 4. Ordnung in $g/mc$ des Diracschen Matrixelements:

(9,6)

${\begin{array}{r|c|c|c|c}&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}&\sum \limits _{\textrm {Perm}}g^{1}g^{2}g^{3}g^{4}&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{2}\right)\\\hline \sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{2}g^{3}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{3}\right)=&0&0&-{\frac {1}{3}}&0\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)g^{1}g^{2}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)=&0&0&+{\frac {2}{3}}&-1\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{1}\right)^{2}=&0&0&-2&3\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{1}g^{3}=&0&-{\frac {1}{2}}&+{\frac {1}{6}}&0\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{1}g^{2}=&0&+1&-1&1\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{3}\right)=&-{\frac {1}{2}}&0&+{\frac {1}{6}}&0\\\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)^{2}=&+1&0&-1&1\end{array}}$

Die linearen Beziehungen zwischen Gliedern wie

$\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}$,

welche den Positronenimpuls $-{\mathfrak {p}}$ enthalten, über den integriert wird, folgen hieraus mit Hilfe ihrer Eigenschaften gegenüber der Winkelmittelung in ${\mathfrak {p}}$:

(9,7)

$\left\{{\begin{aligned}{\overline {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)\left({\mathfrak {pg}}^{3}\right)\left({\mathfrak {pg}}^{4}\right)}}=&{\frac {p^{4}}{3\cdot 5}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{3}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{4}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{3}\right)\right]\\{\overline {{p_{y}}^{2}\cdot \left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)\left({\mathfrak {pg}}^{3}\right)\left({\mathfrak {pg}}^{4}\right)}}=&{\frac {p^{6}}{3\cdot 5\cdot 7}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{3}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{4}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{3}\right)\right]\\{\overline {{p_{y}}^{4}\cdot \left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)\left({\mathfrak {pg}}^{3}\right)\left({\mathfrak {pg}}^{4}\right)}}=&{\frac {p^{8}}{5\cdot 7\cdot 9}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{3}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{4}\right)+\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{4}\right)\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{3}\right)\right]\\{\overline {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)}}=&{\frac {p^{2}}{3}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\\{\overline {{p_{y}}^{2}\cdot \left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)}}=&{\frac {p^{4}}{3\cdot 5}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)\\{\overline {{p_{y}}^{4}\cdot \left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)}}=&{\frac {p^{6}}{5\cdot 7}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right).\end{aligned}}\right.$

Die Behauptung der Eichinvarianz besagt nun, daß in der Tabelle (9,6) der linearen Beziehungen die 4. Spalte (in der Summe über alle Glieder des Diracschen Matrixelements) nicht vorkommt, und die Behauptung der Lorentzinvarianz: daß die ersten drei Spalten (summiert über alle Glieder) im Verhältnis $1:-2:1$ gekoppelt sind (9,5).

Wir verabreden nun (9,5 a), nur die Glieder der zweiten Spalte zu sammeln, d. h. (9‚6; 9,7) im Diracschen Matrixelement nur die Glieder:

(9,8)

$\left\{{\begin{aligned}&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4},\\&\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}\end{aligned}}\right.$

(9,8)

$\left\{{\begin{aligned}&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{1}g^{2}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4},\\&\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{1}g^{2}=\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}\\&\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{1}g^{3}=-{\frac {1}{2}}\cdot \sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4},\\&\sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{1}g^{3}=-{\frac {1}{2}}\cdot \sum \limits _{\textrm {Perm}}\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}\end{aligned}}\right.$

und die, die zu ihnen führen können, auszurechnen und alle anderen fortzulassen.

Unter dieser Vereinfachung erhält man für die Zähler des Diracschen Matrixelements durch Entwicklung von (5,15) nach $g^{i}/mc$ (in derselben Bezeichnungsweise der Übergangswege $\mu =1\dots 6$ durch Spaltenstellen wie in 9,2):

(9,9)

$\left\{{\begin{aligned}{\begin{array}{|c|}Z_{1}\\Z_{2}=Z_{3}\\Z_{4}\\Z_{5}=Z_{6}\end{array}}=&-8{\begin{array}{|c|}0\\0\\0\\1\end{array}}+{\frac {8{p_{y}}^{2}}{{p_{0}}^{2}}}{\begin{array}{|c|}1\\1\\1\\2\end{array}}-8{\frac {{p_{y}}^{4}}{{p_{0}}^{4}}}{\begin{array}{|c|}1\\1\\1\\1\end{array}}\\&-{\frac {4{p_{y}}^{2}}{{p_{0}}^{4}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|c|}3\\2\\1\\4\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|c|}2\\1\\1\\2\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|c|}-1\\-1\\-2\\-2\end{array}}\right]-{\frac {8{p_{y}}^{4}}{{p_{0}}^{6}}}\left({\mathfrak {p}},-2{\mathfrak {g}}^{1}-{\mathfrak {g}}^{2}+{\mathfrak {g}}^{4}\right){\begin{array}{|c|}1\\1\\1\\1\end{array}}\\&-2\left[{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)}{{p_{0}}^{2}}}-{\frac {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)}{{p_{0}}^{4}}}\right]{\begin{array}{|r|}-1\\0\\0\\-1\end{array}}+2\left[{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{4}\right)}{{p_{0}}^{2}}}-{\frac {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{4}\right)}{{p_{0}}^{4}}}\right]{\begin{array}{|r|}0\\0\\1\\1\end{array}}+2\left[{\frac {\left({\mathfrak {g}}^{2}{\mathfrak {g}}^{4}\right)}{{p_{0}}^{2}}}-{\frac {\left({\mathfrak {pg}}^{2}\right)\left({\mathfrak {pg}}^{4}\right)}{{p_{0}}^{4}}}\right]{\begin{array}{|r|}1\\1\\1\\1\end{array}}\\&-2{\frac {{p_{y}}^{2}}{{p_{0}}^{4}}}\left[\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right){\begin{array}{|r|}5\\3\\3\\5\end{array}}+\left({\mathfrak {g}}^{4},{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\right){\begin{array}{|r|}1\\1\\1\\1\end{array}}-{\frac {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)}{{p_{0}}^{2}}}{\begin{array}{|r|}15\\7\\7\\15\end{array}}+{\frac {\left({\mathfrak {pg}}^{4}\right)\left({\mathfrak {p}},{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}\right)}{{p_{0}}^{2}}}{\begin{array}{|r|}1\\1\\1\\1\end{array}}\right]\\&-8{\frac {{p_{y}}^{4}}{{p_{0}}^{6}}}\left[-\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)+{\frac {4\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{4}\right)}{{p_{0}}^{2}}}-2{\frac {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{4}\right)}{{p_{0}}^{2}}}-{\frac {\left({\mathfrak {pg}}^{2}\right)\left({\mathfrak {pg}}^{4}\right)}{{p_{0}}^{2}}}\right]{\begin{array}{|r|}1\\1\\1\\1\end{array}}.\end{aligned}}\right.$

Die Entwicklung geht hier nur bis zur 2. Ordnung, weil die Glieder, die gesammelt werden, zwei Potenzen der Lichtquantenenergien $g^{3}g^{4}\ldots$ enthalten sollen, die nur im Nenner (5,14) vorkommen.

In ähnlicher Weise vereinfacht sich die Entwicklung der reziproken Nenner (5,14):

(9,10)

$\left\{{\begin{aligned}8\cdot {\begin{array}{|c|}N_{1}^{-1}\\N_{2}^{-1}+N_{3}^{-1}\\N_{4}^{-1}\\N_{5}^{-1}+N_{6}^{-1}\end{array}}&={\frac {g^{1}g^{2}}{{p_{0}}^{5}}}{\begin{array}{|r|}6\\12\\-4\\-4\end{array}}+{\frac {g^{1}g^{4}}{{p_{0}}^{5}}}{\begin{array}{|r|}-4\\12\\6\\-4\end{array}}+{\frac {g^{2}g^{3}}{{p_{0}}^{5}}}{\begin{array}{|r|}-2\\0\\-2\\0\end{array}}\\&+{\frac {g^{1}g^{2}}{{p_{0}}^{7}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|r|}-12\\-30\\14\\10\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|r|}-8\\-22\\4\\{\tfrac {7}{2}}\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|r|}3\\8\\-3\\-{\tfrac {7}{2}}\end{array}}\right]\\&+{\frac {g^{1}g^{4}}{{p_{0}}^{7}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|r|}6\\-30\\-18\\8\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|r|}3\\-12\\-3\\{\tfrac {5}{2}}\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|r|}-4\\18\\8\\-{\tfrac {9}{2}}\end{array}}\right]\\&+{\frac {g^{2}g^{4}}{{p_{0}}^{7}}}\left[\left({\mathfrak {pg}}^{1}\right){\begin{array}{|r|}3\\0\\7\\-1\end{array}}+\left({\mathfrak {pg}}^{2}\right){\begin{array}{|r|}2\\-2\\2\\-{\tfrac {1}{2}}\end{array}}+\left({\mathfrak {pg}}^{4}\right){\begin{array}{|r|}-2\\-2\\-2\\-{\tfrac {1}{2}}\end{array}}\right]\\&+{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}}{2{p_{0}}^{7}}}{\begin{array}{|r|}-21\\-30\\9\\5\end{array}}+{\frac {\left({\mathfrak {pg}}^{1}\right)\left({\mathfrak {pg}}^{2}\right)g^{3}g^{4}}{2{p_{0}}^{9}}}{\begin{array}{|r|}91\\70\\-119\\-21\end{array}},\end{aligned}}\right.$

in der die Glieder 0. und 1. Ordnung fortgelassen werden konnten.

Multiplikationen dieser Zähler (9,9) und reziproken Nenner (9,10) ergibt im Gliede 4. Ordnung nach Mittelung über die Positronenrichtung ${\mathfrak {p}}$:

$\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }{\frac {{\overline {Z}}_{\mu }}{N_{\mu }}}=-{\frac {1}{2}}\left[5+{\frac {25}{3}}{\frac {p^{2}}{{p_{0}}^{2}}}-{\frac {231}{3\cdot 5}}{\frac {p^{4}}{{p_{0}}^{4}}}+{\frac {99}{5\cdot 7}}{\frac {p^{6}}{{p_{0}}^{6}}}\right]\sum \limits _{\textrm {Perm}}{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}}{{p_{0}}^{7}}}$

und nach Integration über die Positronenenergie $p_{0}$:

(9,11)

$\left\{{\begin{aligned}H_{in}^{4}&=\sum \limits _{\textrm {Perm}}\sum \limits _{\mu }C\int d{\mathfrak {p}}{\frac {Z_{\mu }}{N_{\mu }}}=-4\pi C\sum \limits _{\textrm {Perm}}{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}}{(mc)^{4}}}\left[{\frac {5}{3\cdot 5}}+{\frac {25}{3\cdot 5\cdot 7}}\right.\\&\left.-{\frac {23}{3\cdot 5\cdot 7\cdot 9}}+{\frac {99}{5\cdot 7\cdot 9\cdot 11}}\right]=-4\pi C\left({\frac {16}{5\cdot 9}}\right)\sum \limits _{\textrm {Perm}}{\frac {\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2}\right)g^{3}g^{4}}{(mc)^{4}}}\end{aligned}}\right.$

Damit ist das verabredete Glied des Diracschen Matrixelements für Streuung von Licht an Licht paralleler Polarisation ausgerechnet. Das Matrixelement des entsprechenden Gliedes der angesetzten Lichtquanten-Wechselwirkung (2,21) ist nach (9,5):

(9,12)

$\alpha {\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}D(-2)\sum \limits _{\textrm {Perm}}\left({\mathfrak {g}}^{1}{\mathfrak {g}}^{2})g^{3}g^{4}\right)$

Gleichsetzung beider Ausdrücke (9,11), (9,12) bestimmt den Koeffizienten $\alpha$ zu

$\alpha =-{\frac {1}{360\pi ^{2}}}$

in Übereinstimmung mit der früheren Rechnung.

§ 10. Diskussion des Resultats

Wir können nun unser Verfahren als bestätigt ansehen und das Resultat folgendermaßen zusammenfassen:

So wie in der gewöhnlichen Maxwellschen Theorie ein Elektron von einem elektromagnetischen Feld, so ist in der Löchertheorie ein Lichtquant von einem Materiefeld umgeben. Die Hamiltonfunktion eines jeden Feldes ist daher die Summe aus den Energien von Licht und Materie, sie enthält die Freiheitsgrade: Feldstärken und Ladungswellen.

So wie aber in dem speziellen Fall, in welchem keine transversalen Lichtquanten da sind und die Elektronen sich so langsam bewegen, daß keine erzeugt werden können, diese Hamiltonfunktion annähernd ersetzt werden kann durch eine Hamiltonfunktion, welche nur noch die Freiheitsgrade der Elektronen enthält (wobei dann die Energie des elektromagnetischen Feldes ersetzt und seine Erzeugung angedeutet wird durch die Coulombsche Wechselwirkung der Elektronen): ebenso kann in dem hier betrachteten Spezialfall, in welchem keine wirklichen Elektronen vorhanden sind und die Energie der Lichtquanten nicht ausreicht, um Elektronenpaare zu erzeugen (0,1), die Energie des Gesamtfeldes annähernd ersetzt werden durch eine Hamiltonfunktion, die nur noch von den Feldstärken ${\mathfrak {E,\ B}}$ allein abhängt:

(10,1)

${\bar {U}}=\int U\ dV\ {\mbox{für}}\ \left\{{\begin{aligned}&|{\mathfrak {D}}|\ll E_{0},\ \left(\mathrm {grad} {\mathfrak {D}}_{i}\right)^{2}-\left({\frac {1}{c}}{\frac {\partial {\mathfrak {D}}_{i}}{\partial t}}\right)^{2}\ll 2\left({\frac {\hbar }{mc}}\right)^{-2}{{\mathfrak {D}}_{i}}^{2}\\&|{\mathfrak {B}}|\ll E_{0},\ \left(\mathrm {grad} {\mathfrak {B}}_{i}\right)^{2}-\left({\frac {1}{c}}{\frac {\partial {\mathfrak {B}}_{i}}{\partial t}}\right)^{2}\ll 2\left({\frac {\hbar }{mc}}\right)^{-2}{{\mathfrak {B}}_{i}}^{2}\end{aligned}}\right\}$

(10,2)

$U={\frac {{\mathfrak {D}}^{2}+{\mathfrak {B}}^{2}}{8\pi }}-{\frac {1}{360\pi ^{2}}}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[\left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}+7({\mathfrak {BD}})^{2}\right]\left(E_{0}={\frac {e}{\left({\frac {e^{2}}{mc^{2}}}\right)^{2}}}\right)$

(10,3)

${\mathfrak {D}}_{i}(\xi ){\mathfrak {B}}_{k}(\xi ')-{\mathfrak {B}}_{k}(\xi '){\mathfrak {D}}_{i}(\xi ){\mathfrak {B}}_{k}=2hci{\frac {\partial }{\partial \xi 'e}}\delta (\xi -\xi ')$

Diese Hamiltonfunktion ${\bar {U}}$ ist als Anfang einer Entwicklung aufzufassen, die nach Potenzen der Feldstärken bis zur 4. Ordnung (entsprechend der Entwicklung der Diracschen Theorie nach der Elektronenladung bis zur 4. Ordnung) und nach dem Grade der Ableitung der Feldstärken bis zur 0. Ordnung durchgeführt ist (entsprechend der Entwicklung der Diracschen Matrixelemente bis zur 4. Ordnung nach Lichtfiequenzen $g^{i}/mc$).

Der Zusatz zur Maxwellschen Energie in (10,2) ist eine Wechselwirkung der Lichtquanten, welcher die virtuelle Materieerzeugung andeutet und die Energie des Materiefeldes ersetzt, welches die Lichtquanten umgibt. Die hier betrachtete Näherung (in der die Ableitungen der Feldstärken vernachlässigt werden) beschreibt eine Nahwirkung der Lichtquanten. Die zu dieser Hamiltonfunktion (10,2) gehörigen kanonischen Gleichungen lauten:

(10,4)

$\left\{{\begin{aligned}&{\frac {1}{c}}{\dot {\mathfrak {B}}}+\mathrm {rot} {\mathfrak {E}}=0,\ \mathrm {div} {\mathfrak {B}}=0;\\-&{\frac {1}{c}}{\dot {\mathfrak {D}}}+\mathrm {rot} {\mathfrak {H}}=0,\ \mathrm {div} {\mathfrak {D}}=0;\\&\qquad {\mathfrak {D}}={\mathfrak {E}}+{\frac {1}{90\pi }}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[4\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {E}}+14({\mathfrak {EB}}){\mathfrak {B}}\right]\\&\qquad {\mathfrak {H}}={\mathfrak {B}}+{\frac {1}{90\pi }}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[4\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {B}}-14({\mathfrak {EB}}){\mathfrak {E}}\right]\end{aligned}}\right.$

oder, in anderer Schreibweise:

(10,5)

$\left\{{\begin{aligned}&{\frac {1}{c}}{\dot {\mathfrak {B}}}+\mathrm {rot} {\mathfrak {E}}=0,\ \mathrm {div} {\mathfrak {B}}=0;\\-&{\frac {1}{c}}{\dot {\mathfrak {E}}}+\mathrm {rot} {\mathfrak {B}}={\frac {4\pi i}{c}},\ \mathrm {div} {\mathfrak {E}}=4\pi \varrho ;\\&{\frac {4\pi i}{c}}={\frac {1}{90\pi }}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[{\frac {1}{c}}{\frac {\partial }{\partial t}}\left[4\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {E}}+14({\mathfrak {EB}}){\mathfrak {B}}\right]-\mathrm {rot} \left[4\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {B}}-14({\mathfrak {EB}}){\mathfrak {E}}\right]\right]\\&4\pi \varrho ={\frac {1}{90\pi }}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\mathrm {div} \left[-4\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right){\mathfrak {E}}-14({\mathfrak {EB}}){\mathfrak {B}}\right].\end{aligned}}\right.$

Sie können auch aus dem Variationsprinzip $\iint LdVdt={\textrm {Extr.}}$ für die Lagrangefunktion

(10,6)

$L={\frac {{\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}}{2}}+{\frac {1}{90\pi }}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left[\left({\mathfrak {E}}^{2}-{\mathfrak {B}}^{2}\right)^{2}+7({\mathfrak {EB}})^{2}\right]$

unter der Nebenbedingung ${\mathfrak {E}}=-{\tfrac {1}{c}}{\dot {\mathfrak {A}}}$, ${\mathfrak {B}}=\mathrm {rot} {\mathfrak {A}}$ hergeleitet werden. In der ersten Fassung (10,4) dieser Gleichungen wird die mit dem Feld gekoppelte virtuelle Materie angedeutet durch ein Auseinandertreten von elektrischer Feldstärke ${\mathfrak {E}}$ und elektrischer Verschiebung ${\mathfrak {D}}$, von magnetischer Induktion ${\mathfrak {B}}$ und der Größe ${\mathfrak {H}}$, ebenso wie in der Elektrodynamik polarisierbarer Körper die wirklich mit dem Feld gekoppelte Materie dargestellt wird.

Bei der zweiten Schreibweise (10,5) tritt die vom Feld ${\mathfrak {E}}$, ${\mathfrak {B}}$ virtuell erzeugte Materie direkt als scheinbare Dichte $\varrho =\varrho ({\mathfrak {E,\ B}})$ und scheinbarer Strom $i=i({\mathfrak {E,\ B}})$ in Erscheinung. Außerdem zeigt diese Ausdrucksweise (10,5), daß die hier angegebenen G1. (10,2 … 10,6) mit den allgemeinen Gleichungen^[16] für Licht und Materie im Einklang sind, in denen nur die Materie $\varrho$, $i$ durch bestimmte Funktionen der Feldstärken, die sie erzeugen, ersetzt ist.

Es gelten, wie man leicht aus (10,2), (10,3) oder (10,4) folgert, die Erhaltungssätze

(10,8)

$\left\{{\begin{aligned}&{\frac {1}{c}}{\frac {\partial U}{\partial t}}+\mathrm {div} {\frac {[{\mathfrak {EH}}]}{4\pi }}=0;&T_{xx}=U-{\frac {1}{4\pi }}\left({\mathfrak {E}}_{y}{\mathfrak {D}}_{y}+{\mathfrak {E}}_{z}{\mathfrak {D}}_{z}+{\mathfrak {H}}_{y}{\mathfrak {B}}_{y}+{\mathfrak {H}}_{z}{\mathfrak {B}}_{z}\right)\\&{\frac {1}{c}}{\frac {\partial }{\partial t}}{\frac {[{\mathfrak {BD}}]_{k}}{4\pi }}+{\frac {\partial }{\partial x_{i}}}T_{ik}=0;\quad &T_{xy}={\frac {1}{4\pi }}\left({\mathfrak {E}}_{x}{\mathfrak {D}}_{y}+{\mathfrak {H}}_{x}{\mathfrak {B}}_{y}\right)\\&&T_{ik}=T_{ki},\ [{\mathfrak {EH}}]=[{\mathfrak {DB}}]\end{aligned}}\right.$

welche zeigen, daß ${\tfrac {[{\mathfrak {EH}}]}{4\pi }}={\tfrac {[{\mathfrak {DB}}]}{4\pi }}$ Energiestrom und Impulsdichte ist im Einklang mit den Formeln der allgemeinen Quantendynamik der Wellenfelder^[16].

Die Gleichungen sind nicht linear, d. h. es entspricht ihnen kein Superpositionsprinzip und sie beschreiben eine Streuung von Licht an Licht, die um so größer wird, je stärker (gegen $E_{0}$) und je kurzwelliger (gegen $\hbar /mc$) die Felder sind.

Den Wirkungsquerschnitt $dQ$ für Streuung von Licht an Licht erhält man, indem man das Quadrat des Matrixelements $H_{in}^{4}$ der Wechselwirkung in (10,2) für den Übergang zweier Lichtquanten mit den Impulsen ${\mathfrak {g}}^{1}$, ${\mathfrak {g}}^{2}$, den Energien $cg^{1}$, $cg^{2}$ und den Polarisationen ${\mathfrak {e}}^{1}$, ${\mathfrak {e}}^{2}$ in zwei andere mit den Impulsen $-{\mathfrak {g}}^{3}$, $-{\mathfrak {g}}^{4}$, den Energien $-cg^{3}$, $-cg^{4}$ und den Polarisationen ${\mathfrak {e}}^{3}$, ${\mathfrak {e}}^{4}$ bildet und es multipliziert mit der Zahl $1/{\mathit {\Delta }}W$ der sekundären Lichtquantenpaare $-{\mathfrak {g}}^{3}$, $-{\mathfrak {g}}^{4}$ pro Energieintervall $c\left(\left|{\mathfrak {g}}^{3}\right|+\left|{\mathfrak {g}}^{4}\right|\right)$ für den Raumwinkel $d\Omega _{4}$ um ${\mathfrak {g}}^{4}$ und es schließlich multipliziert mit ${\tfrac {2\pi }{\hbar }}\cdot {\tfrac {V}{c}}$

${\begin{aligned}dQ=&{\frac {V}{c}}{\frac {2\pi }{\hbar }}{\frac {1}{{\mathit {\Delta }}W}}\left|H_{in}^{4}\right|^{2},\\{\frac {1}{{\mathit {\Delta }}W}}=&d\Omega ^{4}{\frac {V}{ch^{3}}}{\frac {\left|{\mathfrak {g}}^{4}\right|^{2}}{1-\cos {\mathfrak {g}}^{3}{\mathfrak {g}}^{4}}},\\H_{in}^{4}=&-{\frac {1}{360\pi ^{2}}}{\frac {\hbar c}{e^{2}}}{\frac {1}{{E_{0}}^{2}}}\left({\frac {ch\hbar }{V}}\right)^{2}{\frac {1}{\hbar ^{4}}}{\frac {V}{\sqrt {g^{1}g^{2}g^{3}g^{4}}}}{\underset {\begin{array}{c}{\textrm {Perm}}\\1,2,3,4\end{array}}{\sum }}\left\{{\begin{array}{cl}&\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)g^{1}g^{2}g^{3}g^{4}\\-&2\left(\left[{\mathfrak {e}}^{1}{\mathfrak {g}}^{1}\right]\left[{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right]\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)g^{3}g^{4}\\+&\left(\left[{\mathfrak {e}}^{1}{\mathfrak {g}}^{1}\right]\left[{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right]\right)\left(\left[{\mathfrak {e}}^{3}{\mathfrak {g}}^{3}\right]\left[{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right]\right)\\+&7\left|{\mathfrak {e}}^{1}{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right|\left|{\mathfrak {e}}^{3}{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right|g^{1}g^{3}\end{array}}\right\}.\\&\qquad \left({\begin{array}{c}{\mathfrak {g}}^{1}+{\mathfrak {g}}^{2}+{\mathfrak {g}}^{3}+{\mathfrak {g}}^{4}=0\\g_{1}+g^{2}+g^{3}+g^{4}=0\end{array}}\right)\end{aligned}}$

(10,9)

$\left\{{\begin{aligned}&\qquad dQ={\frac {d\Omega ^{4}}{(180\pi )^{2}}}\left({\frac {e^{2}}{mc^{2}}}\right)^{2}\left({\frac {e^{2}}{\hbar c}}\right)^{2}{\frac {1}{(mc)^{6}}}\\&\cdot {\frac {g^{4}}{g^{1}g^{2}g^{3}\left(1-\cos \left({\mathfrak {g}}^{3}{\mathfrak {g}}^{4}\right)\right)}}\left|{\underset {\begin{array}{c}{\textrm {Perm}}\\1,2,3,4\end{array}}{\sum }}\left\{{\begin{array}{cl}&\left({\mathfrak {e}}^{1}{\mathfrak {e}}^{2}\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)g^{1}g^{2}g^{3}g^{4}\\-&2\left(\left[{\mathfrak {e}}^{1}{\mathfrak {g}}^{1}\right]\left[{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right]\right)\left({\mathfrak {e}}^{3}{\mathfrak {e}}^{4}\right)g^{3}g^{4}\\+&\left(\left[{\mathfrak {e}}^{1}{\mathfrak {g}}^{1}\right]\left[{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right]\right)\left(\left[{\mathfrak {e}}^{3}{\mathfrak {g}}^{3}\right]\left[{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right]\right)\\+&7\left|{\mathfrak {e}}^{1}{\mathfrak {e}}^{2}{\mathfrak {g}}^{2}\right|\left|{\mathfrak {e}}^{3}{\mathfrak {e}}^{4}{\mathfrak {g}}^{4}\right|g^{1}g^{3}\end{array}}\right\}\right|^{2}.\end{aligned}}\right.$

Um ein Beispiel zu geben, berechnen wir den Wirkungsquerschnitt für den Fall, daß zwei Lichtquanten gleicher Energie, entgegengesetzter Impulse und gemeinsamer Polarisation aufeinanderstoßen und sich in zwei ebensolche Lichtquanten derselben Polarisation verwandeln. Für die Wellenlänge $\lambda$ und den Streuwinkel $\varphi$ wird dann:

(10,10)

$dQ={\frac {2d\Omega }{5^{2}\cdot 3^{4}}}\left[3+\cos ^{2}\varphi \right]^{2}\left({\frac {e^{2}}{mc^{2}}}\right)^{4}\left({\frac {h}{mc}}\right)^{4}{\frac {1}{\lambda ^{6}}}$.

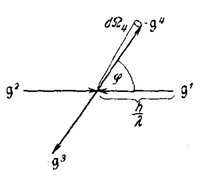Fig. 3

Der Wirkungsradius für Streuung von Licht an Licht ist also von der Größenordnung $10^{-15}$ cm für $\gamma$-Strahlen, $10^{-24}$ cm für Röntgenstrahlen und $10^{-36}$ cm für sichtbares Licht, und wird daher nur schwer experimentell festzustellen sein.

Daß es sich hier (trotz der Darstellung durch klassische Feldfunktionen) um einen rein quantenmechanischen Effekt handelt, wird schon dadurch hervorgehoben, daß der Zusatz in (10,2) proportional zu $h$ ist.

Es ist nun interessant, die hier berechnete Abänderung der Maxwellgleichungen durch die quantentheoretische Möglichkeit der Paarerzeugung mit der von Born^[17] aus Überlegungen innerhalb der klassischen Theorie vorgeschlagenen zu vergleichen.

Bekanntlich hat Born auf Grund der Tatsache, daß die klassischen Maxwellgleichungen eine unendliche Feldenergie um ein Elektron geben, abgeänderte Feldgleichungen angesetzt, in denen er eine Konstante so bestimmen konnte, daß das Feld einer Punktladung $e$ eine Energie $mc^{2}$ bekommt, und hat dann diese Gleichungen in der Weise gequantelt, die durch ihre Eigenschaften als kanonisches System vorgeschrieben ist. Die Bornsche Theorie hat, entwickelt nach Feldstärken, im ersten Glied die Hamiltonfunktion:

(10,11)

${\bar {U}}=\int {\frac {{\mathfrak {B}}^{2}+{\mathfrak {D}}^{2}}{8\pi }}dV-{\frac {(1{,}236)^{4}}{32\pi }}{\frac {1}{{E_{0}}^{2}}}\int \left[\left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}+4({\mathfrak {BD}})^{2}\right]dv$.

Aus Invarianzgründen stimmen die Zusatzglieder zur Maxwellschen Energie in der Bornschen (10,11) und in der Diracschen Theorie (10,2) bis auf Zahlenkoeffizienten überein. Die Zahlenkoeffizienten unterscheiden sich in beiden Theorien um den Faktor

${\frac {4}{45\pi \cdot (1{,}236)^{4}}}{\frac {\hbar c}{e^{2}}}$ für das Glied $\left({\mathfrak {B}}^{2}-{\mathfrak {D}}^{2}\right)^{2}$

und um

${\frac {7}{45\pi (1{,}236)^{4}}}{\frac {\hbar c}{e^{2}}}$ für das Glied $({\mathfrak {BD}})^{2}$.

Wegen des tatsächlichen Wertes der Sommerfeldschen Feinstrukturkonstanten ist der numerische Wert dieses Faktors 1,7_ bzw. 2,9. Und es ist bemerkenswert, daß die quantentheoretische Abänderung der Maxwellschen Gleichungen jedenfalls von der Größenordnung ist, die nach klassischer Vorstellung auf Grund der Selbstenergie zu erwarten wäre.

Diese Übereinstimmung in der Größenordnung bedeutet natürlich noch nicht, daß in der Diracschen Theorie die Frage der Selbstenergie schon gelöst wird, wenn man nur in ihrer Entwicklung nach der Elektronenladung zu genügend hohen Näherungen geht.

Aber sie weist doch darauf hin, daß eine Berücksichtigung der höheren Glieder dieser Entwicklung für die Frage der Konvergenz zu einer anderen Situation führen könnte, als man in den niederen Näherungen findet.

Wie die Gl. (10,2), (10,4) zeigen, braucht es gar nicht immer erlaubt zu sein, die üblich angesetzte Entwicklung der Feldtheorie nach der Elektronenladung $e$ (d. h. hier nach der Feldstärke ${\tfrac {\mathfrak {E}}{E_{0}}}\cdot {\tfrac {\hbar c}{e^{2}}}$) nach dem ersten nichtverschwindenden Glied abzubrechen. Denn die hier angeschriebenen Glieder 4. Ordnung können bei genügend starken (und die nicht mehr angeschriebenen Glieder mit den Ableitungen der Feldstärken können, wie Weisskopf bemerkt hat, bei genügend kurzwelligen) Feldern sehr wohl noch einen Beitrag geben, der von derselben Größenordnung ist, wie der der vorhergehenden Glieder 1., 2. und 3. Ordnung, mit denen man sich bisher bei allen Problemen begnügt hat, d. h. die Entwicklung nach der Kopplung $e$ von Licht und Materie braucht nicht zu konvergieren, wenn (etwa bei schnellen Teilchen oder in der Nähe eines Elektrons) diese Kopplung durch Materieerzeugung zu innig wird.

Man bekommt beinahe den Eindruck^[18], bei der Entwicklung der Strahlungstheorie nach der Elektronenladung etwas Ähnliches vorzunehmen, wie wenn man einen endlichen Ausdruck

$\int \limits _{0}^{1}{\sqrt {1+{\frac {e}{r}}}}dr$

durch eine Entwicklung berechnen würde,

$\int \limits _{0}^{1}{\sqrt {1+{\frac {e}{r}}}}dr=\int \limits _{0}^{1}dr+e\int \limits _{0}^{1}{\frac {dr}{2r}}+e^{2}\int \limits _{0}^{1}{\frac {dr}{-8r^{2}}}+\cdots$,

deren einzelne Glieder um so stärker divergieren, je höher sie sind.

Die Ergebnisse dieser Arbeit deuten also darauf hin, daß man, um in den prinzipiellen Schwierigkeiten der Strahlungstheorie weiter zu kommen, zunächst versuchen muß, die Entwicklung nach $e^{2}/\hbar c$ durch etwas anderes zu ersetzen.

Herrn Prof. Heisenberg möchte ich für seine wesentliche Hilfe und sein ständiges Interesse bei der Arbeit herzlich danken. Ferner danke ich Herrn Kockel für seine Mitarbeit, ohne die die Ausführung der Rechnungen gar nicht möglich gewesen wäre.

Leipzig, Physikalisches Institut der Universität, den 21. Juni 1935.

(Eingegangen 28. Januar 1936)

---

Anmerkungen

1. Dissertation der Philosophischen Fakultät der Universität Leipzig.
   Die vorliegende Arbeit ist die nähere Ausführung zu einer Notiz von Euler und Kockel in den „Naturwissenschaften“. 23. S. 246. 1935. Teil II und III wurde gemeinsam mit Herrn Kockel, § 5 vorwiegend von Herrn Kockel ausgeführt.
2. O. Halpern, Phys. Rev. 44. S. 885. 1934.
3. P. Debye, in einer mündlichen Diskussion mit Herrn Prof. Heisenberg.
4. G. Breit u. J. Wheeler, Phys. Rev. 46. S. 1087. 1934.
5. Die mathematischen Beweise dieses Paragraphen sind identisch mit den von Born (M. Born, M. Born u. L. Infeld, Proc. Roy. Soc. London. A. 143. S. 410. 1933; A. 144. S. 425. 1934; A. 147. S. 522. 1934) benutzten. Sie werden nochmal wiederholt, weil es sich hier um andere physikalische Voraussetzungen handelt. Vgl. auch S. 446.
6. W. Heisenberg u. W. Pauli, Ztschr. f. Phys. 56. S. 1. 1930; 59. S. 168. 1930.
7. Ein Hinzufügen wahrer Ströme, d. h solcher wirklicher Elektronen, die man im Gegensatz zu den hier betrachteten virtuellen (2,3) in der Wilsonkammer sehen würde, die aber nicht an der Strahlung des Feldes teilnehmen und die in dieser Theorie nur als Probekörper vorkommen dürften, zu den Gl. (2,1; 2,12) würde zeigen, daß

   ${\mathfrak {D}}$ die Quellinien wahrer Ladungen,

   ${\mathfrak {H}}$ die Wirbellinien wahrer Ströme beschreibt,

   und würde bestätigen, daß ${\mathfrak {E}}$ die Kraft auf die wahre Ladung und ${\mathfrak {B}}$ die Kraft auf den wahren Strom bedeutet. Vgl. auch C. F. v. Weizsäcker, Ann. d. Phys. 17. S. 869. 1933.

8. W. Heisenberg u. W.Pau1i, Ztschr. f. Phys. 56. s. 1. 1930; 59. S. 168. 1930.
9. Vgl. Fußnote S. 407.
10. Die Matrix (4,12) ist in Anfangs- und Endzustand symmetrisch: $\left(H_{in}^{\ast }=H_{ni}\right)$, wie aus der Symmetrie der Störungen $V_{ik}=V_{ki}^{\ast }$ und aus der Energieerhaltung $E_{i}=E_{n}$ folgt.
11. W. Heisenberg, Ztschr. f. Phys. 90, S. 209. 1934.
12. W. Heisenberg, Ztschr. f. Phys. 90. S. 209. 1934, Formel 59, 60, 61; Ztschr. Phys. 92. S. 692. 1934.
13. $\int \limits _{0}^{\infty }{\frac {p^{m}}{p_{0}^{m+7}}}p^{2}dp={\frac {2}{(m+3)(m+5)}}{\frac {1}{(mc)^{4}}}$.
14. W. Heisenberg u. H. Euler, Ztschr. f. Phys. 98. S. 714. 1936.
15. $\int \limits _{0}^{\infty }{\frac {p^{n}}{p_{0}^{n+5}}}p^{2}dp={\frac {1}{(mc)^{2}}}{\frac {1}{n+3}}$
16. W. Heisenberg u. W. Pauli, Ztschr. f. Phys. 56. S. 1. 1930; 59. S. 168. 1930.
17. M. Born, M. Born u. L. Infeld, Proc. Roy. Soc. London [A] 143. S. 410. 1933; [A] 144. S. 425. 1934; [A] 147. S. 522. 1934.
18. Nach Prof. W. Heisenberg.

Anmerkungen (Wikisource)

1. Vorlage:(8.6
2. In den Spalten Polarisationen wurden in der Vorlage zwei g’s verwendet.